0. 기본 정보

0-A. 개요

python/백준 - 2548번 문제에 대한 분석임.

0-B. 문제 정보

백준 - 2548번: 대표 자연수

---

1. 정답 코드

import sys
input = sys.stdin.readline


n = int(input())
l = list(map(int, input().split()))
l.sort()

mid = len(l)//2 if len(l)%2!=0 else (len(l)//2)-1
print(l[mid])

---

2. 핵심풀이

• numpy 모듈은 쓸 수 없다. (브로드 캐스팅 사용 불가)
• N이 최대 20,000 이므로 이중 for문 사용시 시간초과
• 그렇다면 중앙값을 사용하여 문제를 해결하자.
  • 중앙값이란? 모든 수를 오름차순으로 정렬하였을때 수열의 중간(중앙)에 위치한 값.

2-a. 왜 중앙값인가?

• 가정: 크기가 n인 정렬된 list L과 L의 중앙값을 m이라 할때

  • $f(x) = \sum_{i=0}^{n-1}|L[i]-x|$ 에서 $f(x)$의 최소값이 되는 x값은 중앙값인 m이다.
  • ($i$ = list L의 index)
  • $x$ = list L의 원소 중 하나

• $m>x일 경우$
  $f(x) = \sum_{i=0}^{n-1}|L[i]-x|$에서
  x가 m보다 작아질 경우
  x의 index보다 더 낮은 구간의 차이의 합은 줄어들지만
  x의 index보다 더 높은 구간의 차이의 합이 증가한다.
  단, 여기서 x는 중앙값 m보다 더 작은 수이기 때문에 (값도 index도 전부 작기 때문에)
  차이의 합이 줄어드는 구간보다 차이의 합이 증가하는 구간이 더 커지므로
  $f(x)$는 증가한다.

• $m<x일 경우$
  위 경우와 정확히 반대이다.
  $f(x) = \sum_{i=0}^{n-1}|L[i]-x|$에서
  x가 m보다 커질 경우
  x의 index보다 더 낮은 구간의 차이의 합은 증가하지만
  x의 index보다 더 높은 구간의 차이의 합이 줄어든다.
  단, 여기서 x는 중앙값 m보다 더 큰 수이기 때문에 (값도 index도 전부 크기 때문에)
  차이의 합이 줄어드는 구간보다 차이의 합이 증가하는 구간이 더 커지므로
  $f(x)$는 증가한다.

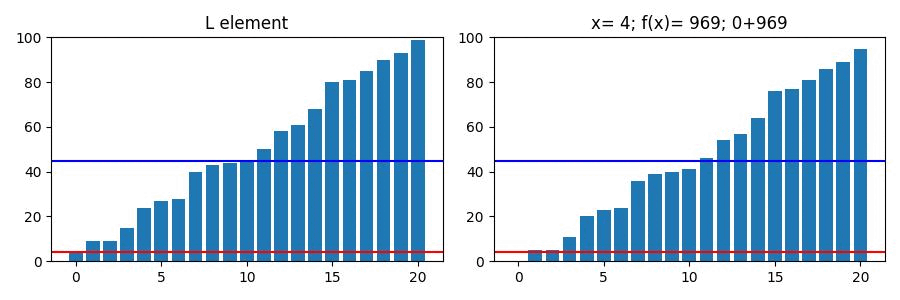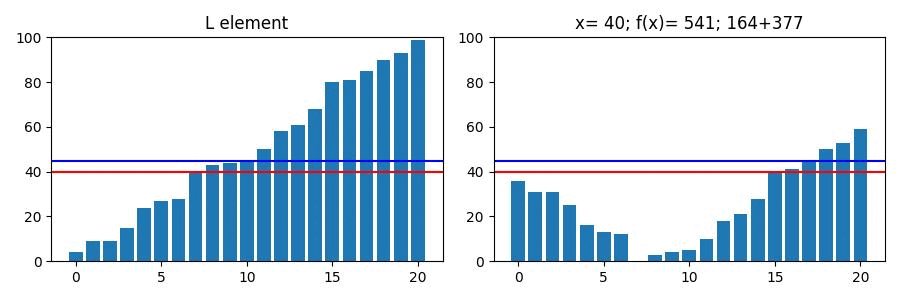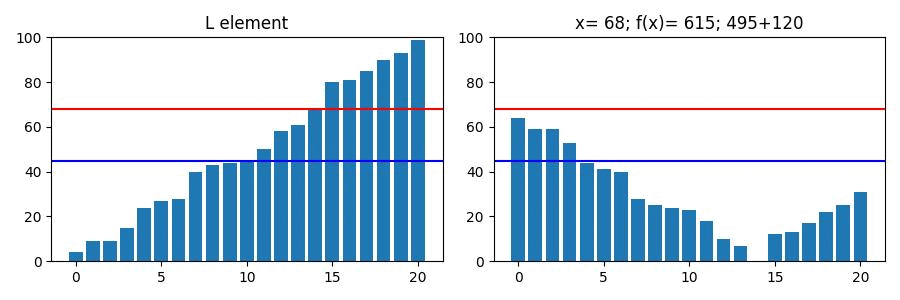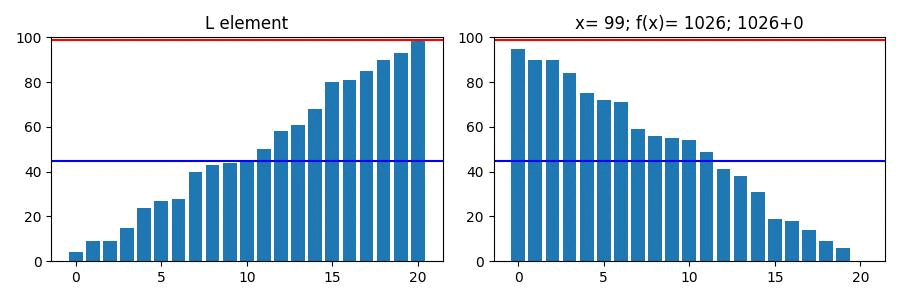
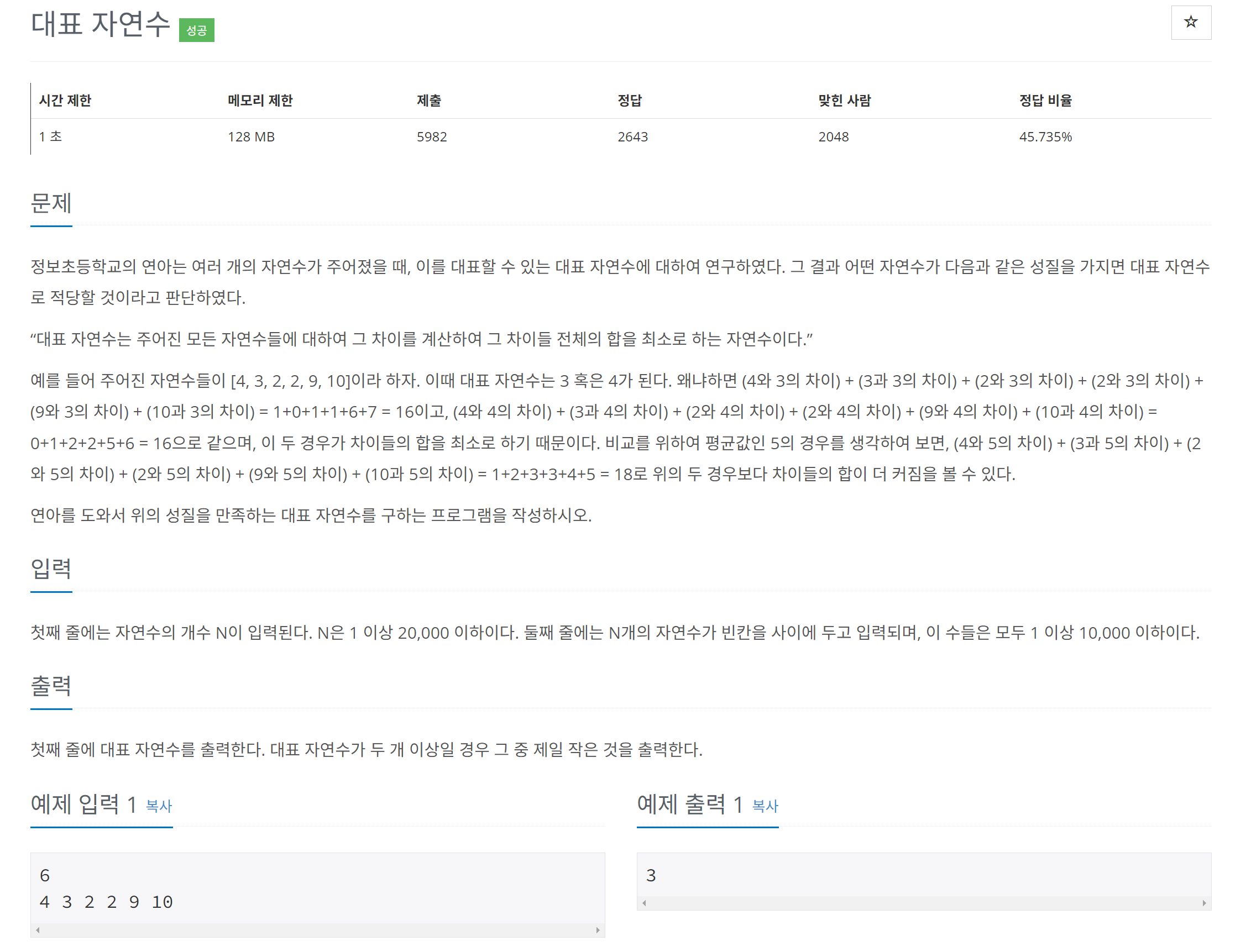
아래 그림은 크기가 20이고 등차가 1인 List의 $f(x)$값이 최소값인 순간이다.

보시다시피 $x$가 중앙값일때 $f(x)$의 값도 최소가 된다.
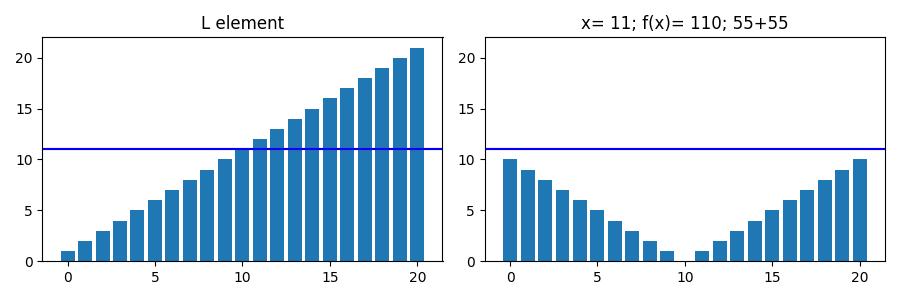
아래는 위 List의 $x$값에 따른 $f(x)$변화량이다.

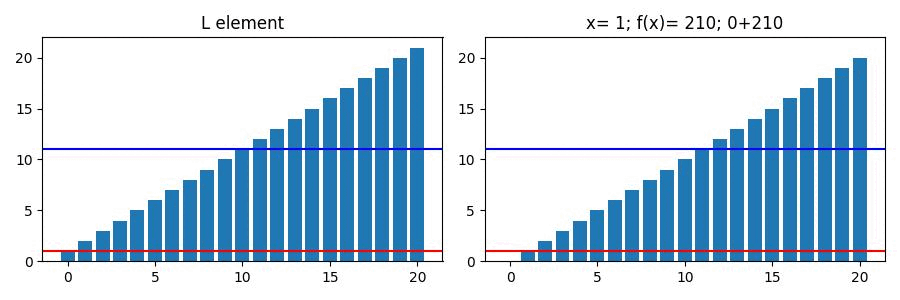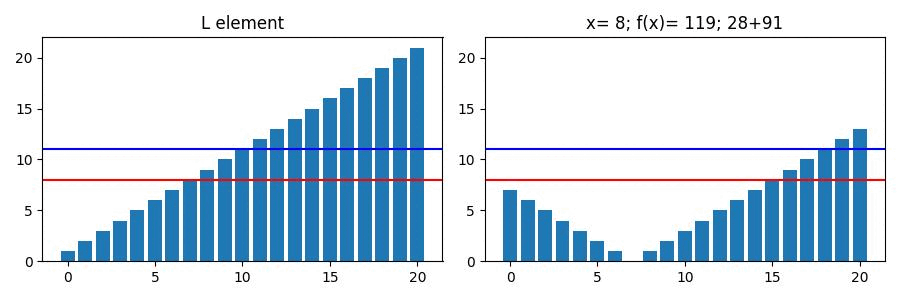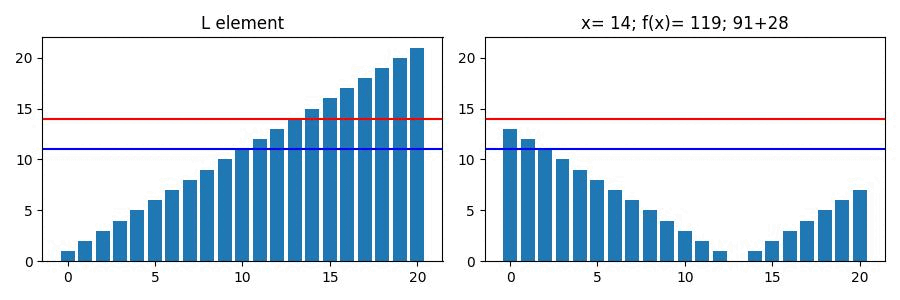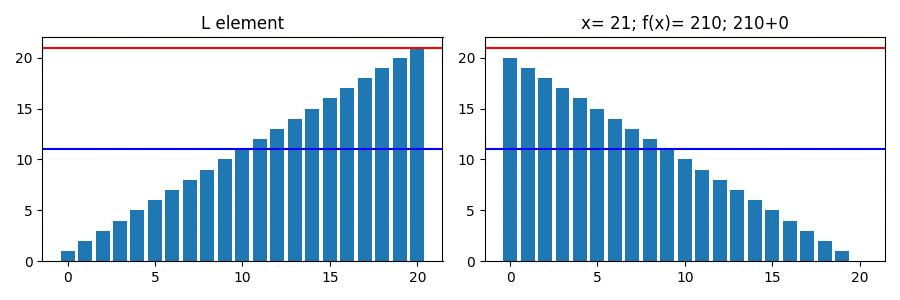
파란색 선이 $f(x)$가 최소가 되는 값(중앙값)이며
빨간색 선은 List의 요소 하나씩 $f(x)$에 대입한 결과이다.
또한 우측 title을 보면 x의 인덱스보다 더 낮은 구간과 높은 구간의 합을 각각 볼 수 있다.

2-b. 왜 중앙값인가?(실제 예시)

자세한 설명은 위에서 다 했으므로
실제 예시로만 들며 빠르게 설명하겠다.

아래는 정렬된 크기가 20인 list L이다.
L = array([ 4, 9, 9, 15, 24, 27, 28, 40, 43, 44, 45, 50, 58, 61, 68, 80, 81, 85, 90, 93, 99])
m = 45

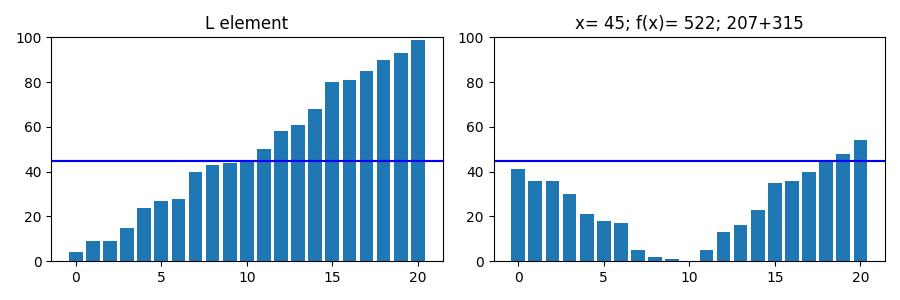
이역시 $x$가 중앙값일때 각 원소의 차이의 합이 최소값이 된다.