합병(병합) 정렬 (Merge Sort)

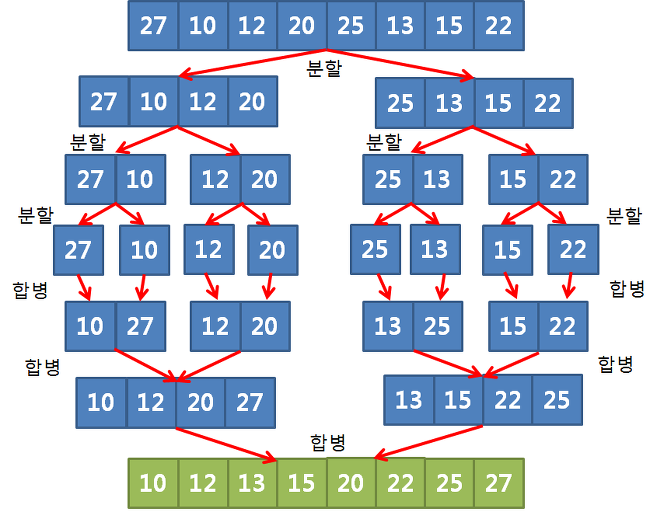
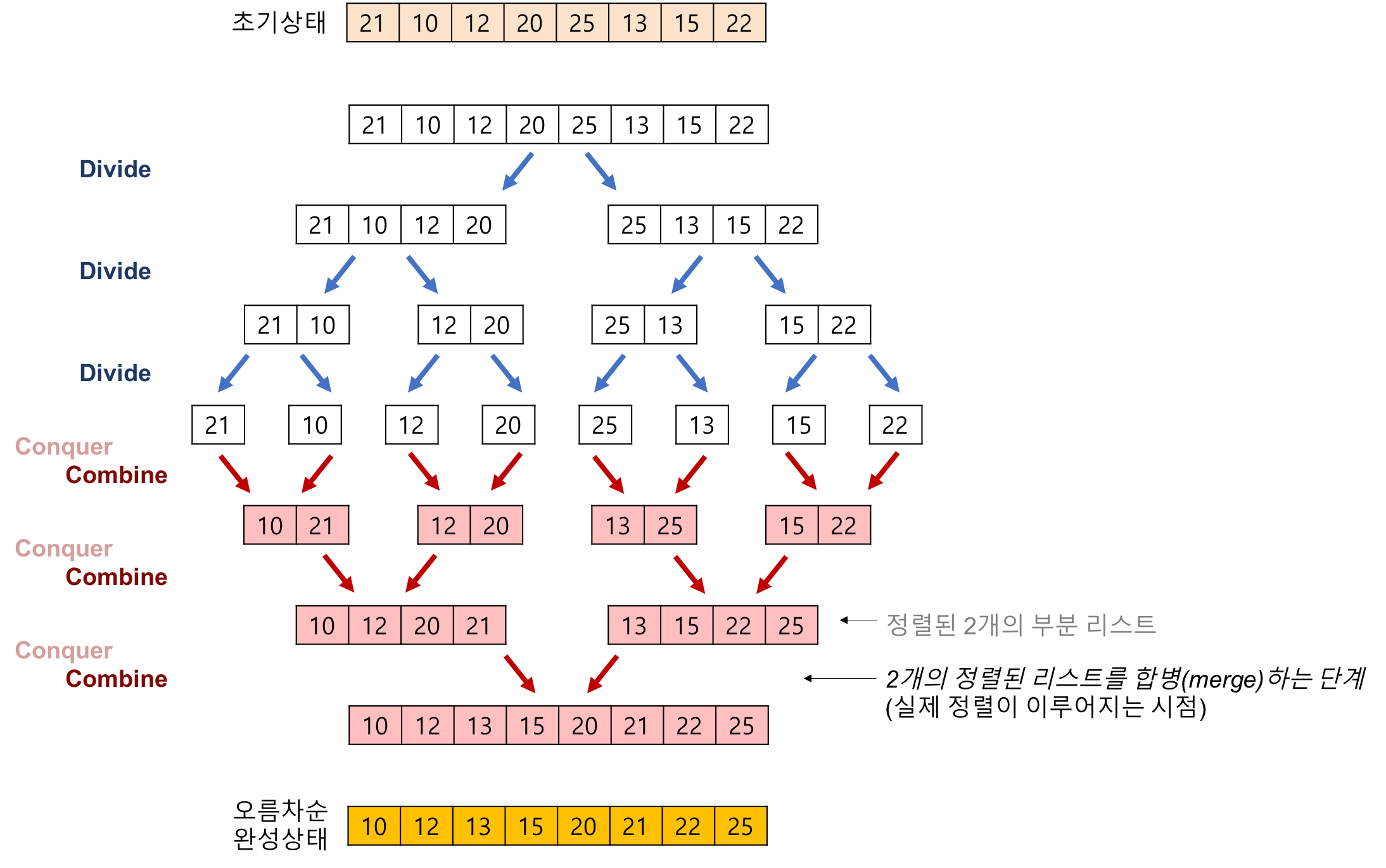
분할 정복 알고리즘을 이용
(문제를 작은 2개의 문제로 분리한 후, 해결한 다음, 결과를 모아 원래의 문제를 해결)

데이터의 분포에 영향을 덜 받아, 입력 데이터가 무엇이든 정렬되는 시간은 동일하다.

시간 복잡도는 O(nlogn) 이다.

---

정렬 방법

1. 주어진 리스트를 절반으로 분할하여 부분리스트로 나눈다. (Divide : 분할)

2. 해당 부분리스트의 길이가 1이 아니라면 1번 과정을 되풀이한다.

3. 인접한 부분리스트끼리 정렬하여 합친다. (Conqure, Combine : 정복, 결합)

---

자바로 구현하면 다음과 같다.

class Main {

  static int[] newArr;
  public static void main(String[] args) {
      int[] arr = { 9, 8, 7, 6, 5, 4, 3, 2, 1 };

      newArr = new int[arr.length];

	  merge_sort(Arrays.copyof(arr, arr.length), 0, arr.length -1);
      
      System.out.println(Arrays.toString(newArr));
  }

  static void merge_sort(int[] arr, int left, int right) {
      if (left == right) {
          return;
      }

      int mid = (left + right) / 2;

      merge_sort(arr, left, mid);
      merge_sort(arr, mid + 1, right);

      merge_sort(arr, left, mid, right);
  }

  static void merge_sort(int[] arr, int left, int mid, int right) {
      int start = left;
      int end = (mid + 1);
      int idx = left;

      while (start <= mid && end <= right) {
          if (arr[start] > arr[end]) {
              newArr[idx] = arr[start];
              start++;
              idx++;
          } else {
              newArr[idx] = arr[end];
              end++;
              idx++;
          }
      }

      if (start > mid) {
          while (end <= right) {
              newArr[idx] = arr[end];
              end++;
              idx++;
          }
      } else {
          while (start <= mid) {
              newArr[idx] = arr[start];
              start++;
              idx++;
          }
      }


      for (int i = left; i <= right; i++) {
          arr[i] = newArr[i];
      }
  }
}

---

참조한 책 및 사이트

https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html