[알고리즘] 02. Efficiency of Algorithm

jmt·2024년 3월 23일

알고리즘

목록 보기

2/18

경북대 COMP0319 강의 기반의 정리
Introduction to algorithms 3판 참고

Analyzing Algorithms

지난 시간에 이어 알고리즘의 효율성(efficiency of algorithm)에 대해 알아보자. 알고리즘의 효율성을 따지기 위해서 알고리즘을 분석해봐야 한다. 이 과정을 통해 알고리즘이 얼마나 효율적인지, 즉 메모리와 같은 하드웨어 장치를 얼마나 사용하는지와 계산 시간(computational time)이 얼마나 걸리는지를 알아볼 수 있다.

Analysis of Insertion Sort

삽입 정렬이 얼마나 효율적인지 따져보자. 삽입 정렬의 코드 한 줄마다 소모되는 비용과 시간을 표현하면 다음과 같다.

여기서 $t_i$ 는 비교 횟수라고 보면 된다. 총 실행시간 $(=T(n))$ 을 계산해보면 다음과 같다.

$T(n)$

\begin{aligned} T(n) = c_1n &+ c_2(n-1) + c_4(n-1) + c_5\sum^n_{j=2}t_j + c_6\sum^n_{j=2} (t_j-1). \\&+ c_7\sum^n_{j=2} (t_j-1) + c_8(n-1).\\ \end{aligned}

Best case

복잡해보이는데, 만약 비교 횟수가 1이면 어떨까? 비교 횟수가 1이라는 의미는 이미 배열 $A$ 가 정렬되어 있는 상태를 의미한다. 그럼 $T(n)$ 은 다음과 같다.

T(n) = (c_1+c_2+c_4+c_5+c_8)n - (c_2+c_4+c_5+c_8).

Worst case

그럼 최악의 경우는 언제일까? 역순으로 정렬된 경우이다. 이 때는 비교횟수 $t_j$ 가 $j$ 가 된다. 역순이면, 1부터 $j-1$ 까지 전부 비교를 해봐야 하기 때문이다. 그럼 시그마는 다음과 같이 표현될 것이고,

\begin{aligned} \sum^n_{j=2} t_j &= \sum^n_{j=2} j = \frac{n(n+1)}{2} -1\\ \sum^n_{j=2} (t_j-1) &= \sum^n_{j=2} (j-1) = \frac{n(n+1)}{2} \end{aligned}

$T(n)$ 은 다음과 같다.

T(n) = (\frac{c_5}{2} + ...)n^2 + (c_1 + c_2 + ...)n - (c_2 + c_4 + ...)

$T(n)$ 을 구해보고 Best case, Worst case로 나눠 계산해본 결과, 삽입 정렬은 input size, $n$ 에 대해 의존적이라는 사실을 알 수 있다. 그런데 실제로 알고리즘의 효율성을 따질 때 상한선(upper bound)를 고려한다. 즉, worst case를 고려해야 한다. 그 이유는 실제로 worst case인 경우가 빈번하게 나타나기 때문이다.

결론

삽입 정렬을 이용해 크기가 $n$ 인 배열 $A$ 를 정렬하면, 총 계산시간이 최악의 경우 $n^2$ 걸린다는 사실을 알았다. 별로 크지 않아 보이지만, $n=10000$ 이면... 상당히 많은 시간이 걸린다는 것을 알 수 있다.

Merge Sort

알고리즘을 디자인 하는 방법은 여러가지가 있다. 그 중 병합 정렬(merge sort)는 "divide-and-conquer"라는 기법을 이용해 정렬 문제를 해결하는 알고리즘이다. 삽입 정렬의 경우에는 점진적인 방법(incremental approach)을 사용한 것이다.

Divide-and-Conquer

병합 정렬을 3가지로 나눠보자.

Divide : 정렬할 $n$ 개의 요소를 가지는 배열을 각각 $n/2$ 개의 요소를 가지는 두 개의 배열로 나눈다.
Conquer : 2개의 하위 배열을 재귀적인 방법으로 각각 정렬한다.
Combine : 2개로 나뉜 하위배열을 하나의 정렬된 배열로 합친다.

Merge

병합 정렬에서 가장 핵심적인 부분은 "combine"(=merge)과정이다. 2개의 정렬된 배열을 하나로 합칠 때 어떻게 구현할 지를 알아보자.

예를 들어 2개의 정렬된 카드 더미가 있다고 가정해보자. 각 더미에서 카드는 위를 향하게 되어 있으며(숫자를 확인할 수 있다.), 가장 위에 있는 카드 중 더 작은 놈을 골라서 테이블 위로 보낸다. 여기서 테이블이 최종적인 정렬된 배열이 된다. 둘 중 하나의 더미가 비게 되면 나머지 더미에 있는 카드들을 순차적으로 테이블로 보낸다.

비어있는지는 어떻게 확인할까? 각 더미의 맨 아래에 "Sentinal Card"를 추가한다. Sentinal card의 값을 $\infin$ 으로 표시하고 두자. 그럼 둘 중 하나의 더미에 있던 카드가 전부 나오면, 마지막 sentinal card가 나오게 된다. $\infin$ 보다 큰 값은 없을테니 당연히 나머지 더미 카드를 계속 고르게 된다.

A가 정렬할 배열이고, $p$ 는 배열의 첫번째 인덱스, $r$ 은 마지막 인덱스, $q$ 는 중간값이다. $q = (p+r)/2$ . 이 때, line 8, 9가 위에서 설명한 sentinal card를 넣는 과정이 된다.

Loop Invariant of Merge

그럼 위 병합 과정의 루프 불변성을 따져보자. 병합 정렬은 위 Merge를 크기가 1인 배열이 될 때까지 계속 2개로 나누고(divide), 그 때 recursion bottoms out! 하게 되면서 Merge 과정을 통해 하나의 정렬된 배열을 완성한다. 그렇기에 병합 과정의 루프 불변성을 따지면 병합 정렬이 올바른 알고리즘인지 타당성을 따질 수 있게 된다.

초기조건 : for문에서 $k=p$ 일 때가 가장 처음 실행될 때다. 이 때 배열 $A[1...k-1]$ 은 비어있는 상태이고, $L$ 과 $R$ 의 하위 배열을 통해 가장 작은 값이 A[1]에 추가된다. 그러므로 초기조건은 만족한다.
유지조건 : for문을 돌면서 line13의 경우와 16의 경우를 나눠 생각해보자.
2.1 $L[i] \le R[j]$
현재가 $k$ 번째라고 가정하자. line14 실행 전까지 $A[p...k-1]$ 은 정렬된 상태이고, 현재 두 개의 정렬된 배열 중 작은 값은 $L[i]$ 를 line14를 실행하게 되면서 $A[p...k]$ 의 배열은 정렬된 상태가 된다. 그리고 $k$ 값이 1증가 되고 $i$ 값도 1 증가되면서 $k+1$ 번 째에도 동일한 반복이 수행되기 때문에 loop invariant가 성립한다!
2.2 $L[i] > R[j]$
2.1의 과정을 동일하게 수행하므로 이 때도 loop invariant가 성립한다.
종료조건 : $k=r+1$ 일 때 종료된다. $A[p...r]$ 까지 정렬된 상태이므로 Merge 알고리즘은 타당하다 볼 수 있다!

최종적으로 우리는 Merge 알고리즘의 타당성을 증명했다. 총 $p$ 부터 $r$ 까지 반복문을 돌면서, 문제의 크기 $n$ 을 $n=r-p+1$ 이라 정의하면 Merge는 총 $n$ 번 수행된다는 것도 알 수 있다. 그렇다면 병합 정렬(Merge Sort)를 아래와 같이 표현할 수 있다.

Merge Sort Code

$p=r$ 일 때, 즉 크기가 1인 하위 배열이 되면 line3, 4가 더 이상 실행되지 않으면서 위에서 설명한 Recursion bottoms out!되고, Merge과정을 계속 수행하면서 하나의 정렬된 배열을 완성시킨다.

Analysis of Merge Sort

$T(n)$

이제 병합 정렬의 효율성을 따져보기 위해 분석해보자. 앞서 삽입 정렬을 통해 크기가 $n$ 인 문제를 해결하는데 걸리는 총 계산 시간을 $T(n)$ 으로 나타냈다.
병합 정렬은 2개의 하위 배열로 나누고 나눌 때마다 combine(=merge)하면서 cost가 소모될 것이다. 그리고 2개의 하위 배열로 나눌 때의 각 하위 배열을 정렬하는 시간은 $T(n/2)$ 가 된다. 그러므로 다음과 같이 병합 정렬이 재귀호출을 통해 수행되는 총 연산시간 $T(n)$ 을 다음과 같이 나타낼 수 있다.

\begin{aligned} T(n) = \begin{cases} c\quad\quad\quad\quad\quad\quad\;\,(n=1) \\ 2T(n/2) + cn\quad(n>1) \end{cases} \end{aligned}

뒤의 $cn$ 이 combine(=merge)하면서 발생되는 cost이다.

재귀 트리(Recursion tree)

이런 재귀적인 방식을 재귀 트리(recursion tree)로 나타낼 수 있다. 아래와 같다.

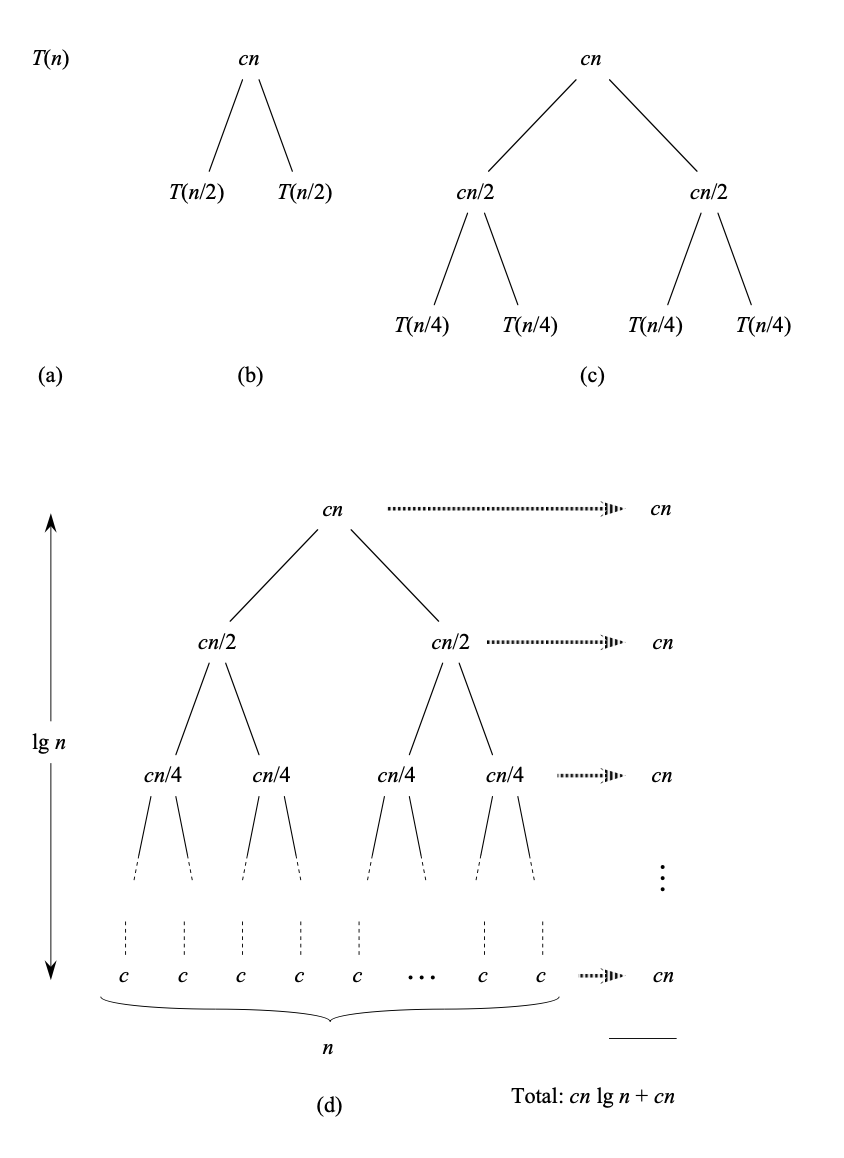
(a)에서 (c)로 가면서 병합 정렬처럼 하나의 문제를 2개로 나누게 된 경우 트리의 구조를 따라 총 연산을 나타낸 것이다. 전체적인 트리가 바로 (d)에 해당한다. (d)를 보면 총 계산시간이 $cn \log n + cn$ 이라는데 이는 왜 그럴까? 문제의 총 갯수를 먼저 살펴보자. 트리의 깊이(= $h$ )가 1씩 내려갈 때마다 2배로 늘어나기에 문제의 총 갯수는 $2^h$ 라고 할 수 있다. 문제의 총 크기가 $n$ 이므로 총 $n$ 개의 크기를 가지는 단계까지 내려가야하는데, 수식으로 정리하면,
문제의 총 크기는 $2^h$ 이고 $2^h = n$ 이므로, $h=\log_2 n$ 이 된다.

즉 트리의 level은 $\log_2 n + 1$ 이다.
소모되는 cost는 마지막을 제외하고 모두 $cn$ 이고, 마지막의 cost는 $c$ 이므로 최종적으로 $\log_2 n$ 번만큼 $cn$ 의 비용을 가지고 마지막으로 $cn$ 의 비용을 소모해야 하므로, 총합은 $cn\log_2 n + cn$ 이 된다.

결론

앞서 삽입 정렬은 총 계산 시간, $T(n)$ 은 최악의 경우에 $n^2$ 이라 하였다. 반면 병합 정렬은 $cn \log_2 n + cn$ 의 총 비용을 가지게 된다. 직감적으로 병합 정렬의 계산 시간이 더 짧기에 효율적이라 볼 수 있지만, 병합 정렬의 경우 재귀 호출을 통해 정의되는 알고리즘이므로 최악의 경우를 어떻게 따져볼까? 이를 알아보기 위해 다음 시간에는 점근적 표기법(Asymptotic Notation)에 대해 배워보자.

jmt

고분자/컴공

이전 포스트

[알고리즘] 01. What is algorithm?

다음 포스트

[알고리즘] 02. Efficiency of Algorithm

알고리즘

Analyzing Algorithms

Analysis of Insertion Sort