Big-O Notation 빅 오 표기법
알고리즘의 시간 복잡도를 나타내는 표기법이다.
길게 설명하는 것보다 표기법으로 설명하면 시간복잡도를 빠르게 설명할 수 있다.
그리고 알고리즘 분석을 빠르게 할 수 있고, 언제 무엇을 쓸지 파악하며 자신의 코드를 평가할 수 있다.
시간복잡도 3가지 표기법
- Big-O(빅-오) : 최악의 경우
- Big-Ω(빅-오메가) : 최선의 경우
- Big-θ(빅-세타) : 평균의 경우
Big-O(빅-오) 표기법을 사용하는 이유는 최악의 시간을 대비하는 것이 바람직하기 떄문이다. 왜냐하면 최선의 경우를 고려했어도 최악의 경우가 발생할 수 있기 때문이다.
특징
1. 상수(Constant)항을 무시한다
O(2N)❌ O(N)⭕
n이 무한대로 켜졌을때 상수는 무의미하므로 상수 2는 무시한다
2. 작은 항은 무시하고, 최고차항만 표시한다
O(8n^2 + 8n + 8)❌ O(n^2)⭕
n이 무한대로 켜졌을 때, 상수항은 의미가 없어져서 무시하고, 8n도 n이 켜지면 8n^2이 차지하는 비중이 더 크므로 무시한다. 따라서 상수항을 무시하고 최고차항을 표시하면 O(n^2)이 된다.
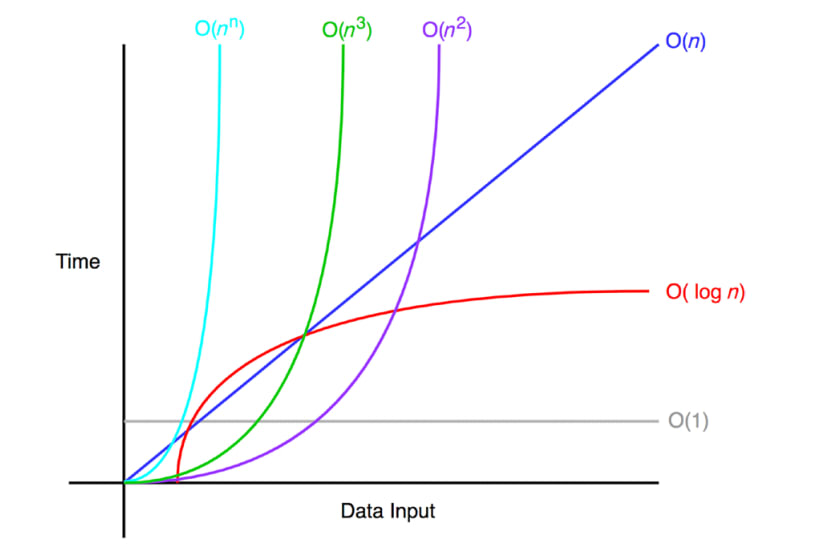
표기법 종류
순위가 위에 있을 수로 더 좋다.
| 순위 | Big-O notation |
|---|---|
| O(1) | 상수시간. (입력크기와 상관없이 연산횟수 고정) |
| O(logN) | 로그. (입력크기 증가율 > 연산횟수 증가율) |
| O(N) | 선형. (입력크기 & 연산횟수 비례) |
| O(NlogN) | 로그선형. (입력크기 2배 증가시 연산횟수 2배 조금 넘어서 증가) |
| O(N²) | 이차. (입력크기n 연산횟수n²) |
| O(N³) | 삼차. (두 n Χ n 행렬의 곱) |
| O(Cⁿ) | 지수. (지수적으로 증가/ 여행하는 외판원 문제, 집합 분할 문제) |
O(1) Constant time
상수시간 복잡도
-
입력크기 n이 얼마나 크던 상관없이 고정된 단계횟수로 끝내기 때문에 가장 효율적이다.
-
Stack의 push, pop
function exampleConstantFunc(n) { return n*n; }function O_1_algorithm(arr, index) { return arr[index]; } let arr = [1, 2, 3, 4, 5]; let index = 1; let result = O_1_algorithm(arr, index); console.log(result); // 2
O(log n) Logarithmic time
로그시간 복잡도
- 입력크기 n이 증가하는 양에 비해 연산스텝이 비교적 적게 일어난다
- 로그(Logarithmic)는 지수(exponent)의 정반대다
- 이진검색 알고리즘, up & down
Q. n = log(밑이 2) 32 에서 n은?
32 % 2 = 16 1번
16 % 2 = 8 2번
8 % 2 = 4 3번
4 % 2 = 2 4번
2 % 2 = 1 5번
n = 5
=> 5 = log 32 (**특성상 log밑 2는 사라짐)
이 문제에서 보듯이 반으로 쪼개는 이진검색과 유사하다
O(n) Linear time
선형시간 복잡도
- 입력값 n이 증가하면 스텝도 n번 증가하여 실행한다
- ex) 입력값 1이면 1초, 100배 증가하면 100초가 걸리는 알고리즘
- for문 예제
function exampleLinear(n) {
for (var i = 0 ; i < n; i++ ) {
console.log(i)
}
}
function O_n_exampleLinear(n) {
for (let i = 0; i < 2n; i++) { // 시간 2초씩 증가
console.log(i)
}
}O(n log n)
- 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap Sort)
- 입력크기 2배 증가하면 연산횟수 2배 조금 넘게 증가한다
O(n²) Quadratic time
2차시간 복잡도
- 입력값 n에 의해서 n 제곱수 비율로 증가하여 n²번 실행한다
- ex) 입력값 1일때 1초였는데, 입력값 5주면 25초가 걸리는 것
- 중첩반복 Nested Loops 있을 때 발생한다
- 이중 for 문, 삽입정렬(insertion sort), 버블정렬(bubble sort), 선택정렬(selection sort) 과 같은 비효율 정렬 알고리즘이 해당된다
//ex1
function quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}
//ex2
for (int i = 0; i < n; i += c) {
for (int j = 0; j < n; j += c) {
// some O(1) expressions
}
}O(2ⁿ) Exponential Time
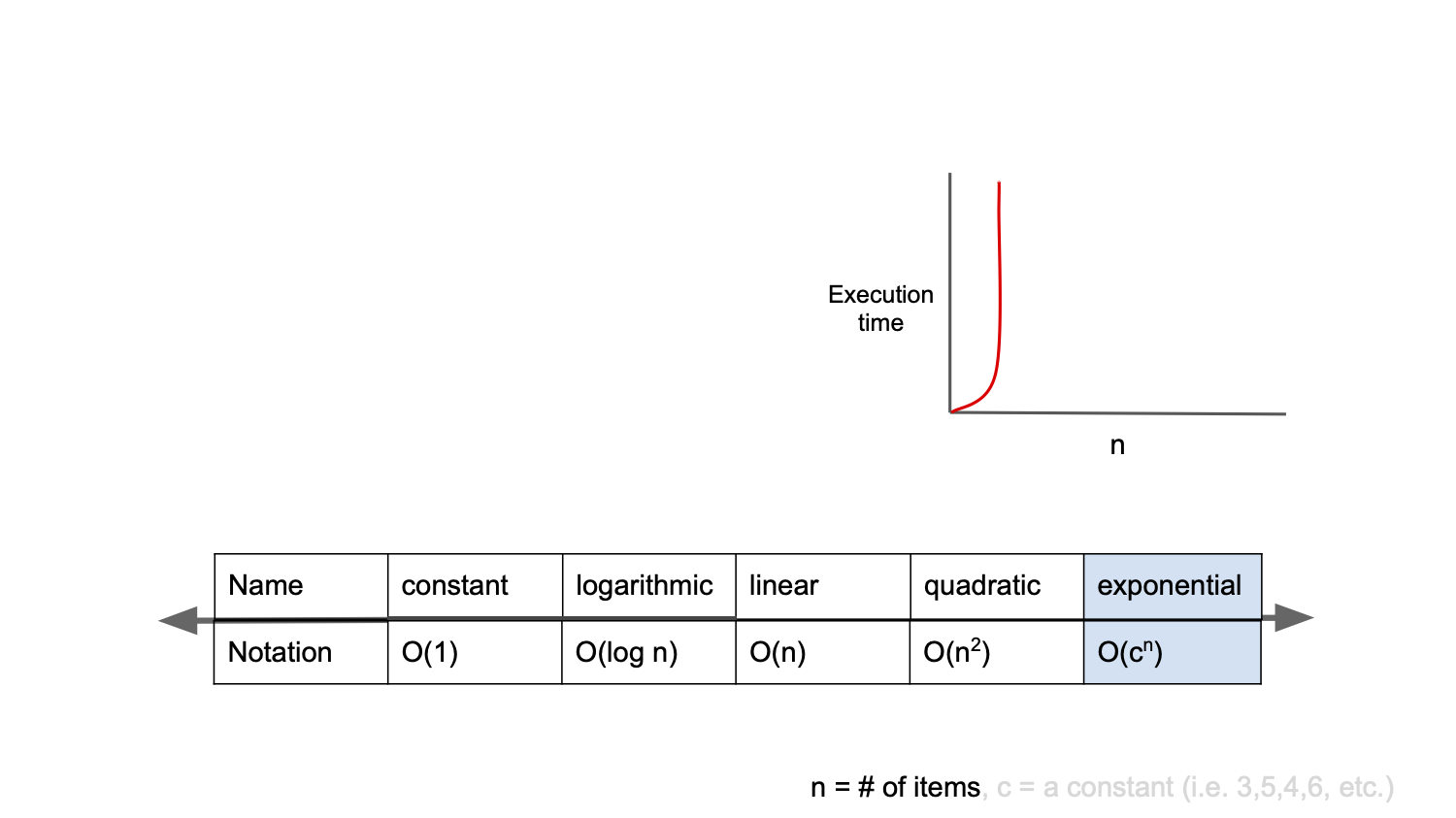
- 가장 느린 시간 복잡도
- ex) 종이 접을 때마다 두께가 2배로 늘어나는 것
// 피보나치 수열 재귀로 구현한 예제
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}시간복잡도 기능순
O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ) < O(n!)
- 오른쪽으로 갈수록 효율성이 떨어진다
트레이드오프 관계
시간과 공간이 트레이드오프 관계다
실행이 빠르면 공간을 많이 차지하고, 공간이 적으면 실행이 느리다는 것이다.
대부분의 경우 트레이드오프의 관계가 있으며 알고리즘의 특징이다.
데이터크기에 따른 시간복잡도
문제마다 시간 복잡도를 예상해서 풀 수 있다.
| 데이터 크기 제한 | 예상되는시간 복잡도 |
|---|---|
| n ≤ 1,000,000 | O(n) or O (logn) |
| n ≤ 10,000 | O(n2) |
| n ≤ 500 | O(n3) |
요구사항에 따른 알고리즘 설계
- N범위가 500인 경우 - 시간복잡도 O(n3) 알고리즘 설계
- N범위가 2000인 경우 - 시간복잡도 O(n2) 알고리즘 설계
- N범위가 100,000인 경우 - 시간복잡도 O(nlogn) 알고리즘 설계
- N범위가 10,000,000인 경우 - 시간복잡도 O(n) 알고리즘 설계
참고
Understanding Big-O Notation With JavaScript

