결론

// 최대공약수
const gcd = (a, b) => a % b ? gcd(b, a % b) : b;
// 최소공배수
const lcm = (a, b) => a * b / gcd(a, b);

GCD

최대공약수(Greatest Common Divisor, GCD)
: 두 수 이상의 여러 공약수 중 최대인 수

• 약수(Divisor) : 주어진 수를 나누어 떨어지게 하는 수

• 공약수(CD: Common Divisor) : 두 수 이상의 여러 수 중 공통된 약수.

구현방법

• 소인수분해 시간복잡도 : O(N)
• 유클리드호제법 O(log N)

<예시>

6의 약수: 1, 2, 3, 6
9의 약수: 1, 3, 9

• 6과 9의 공약수는 1, 3이다
• 6과 9의 최대공약수는 3이다

구현코드

• i가 2부터 두수의 min까지 모든 정수로 나누어 보기

let gcd = (num1, num2) => {
    let gcd = 1;
    for(let i=2; i<=Math.min(num1, num2); i++){
        if(num1 % i === 0 && num2 % i === 0){
            gcd = i;
        }
    }
    return gcd;
}

LCM

최소공배수(Lowest Common Multiple, LCM)
: 두 수 이상의 여러 공배수 중 최소인 수

• 공배수(CM: Common Multiple) : 두 수 이상의 여러 수 중 공통된 배수.
• 배수(Multiple) : 하나의 수에 정수를 곱한 수
  반대로, 배수는 그 수에 의해 나누어 떨어지는 수
  • 배수가 많으므로 최대공배수는 구할 수 없음

<예시>

12의 배수 : 12, 24, 36, 48, 60, 72, 84 ...
18의 배수 : 18, 36, 72, 90 ...

• 12와 18의 공배수는 36, 72
• 12와 18의 최소공배수는 36

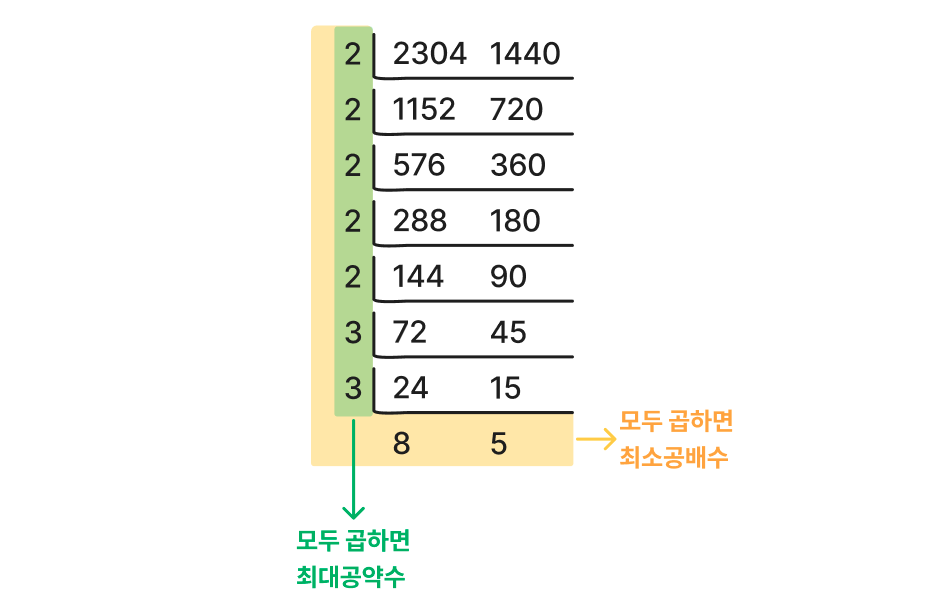
소인수분해

최대공약수를 구할 때 밑처럼 소인수분해로 구할 수 있다.
문제는 모든 정수를 나눠야해서 시간복잡도가 O(N)이 된다.
그리고 수가 클 때 계산이 복잡해져서 약수를 한번에 찾기 힘들어진다.
그럴 때 유클리드 호제법으로 빠르게 최대공약수를 구할 수 있다.

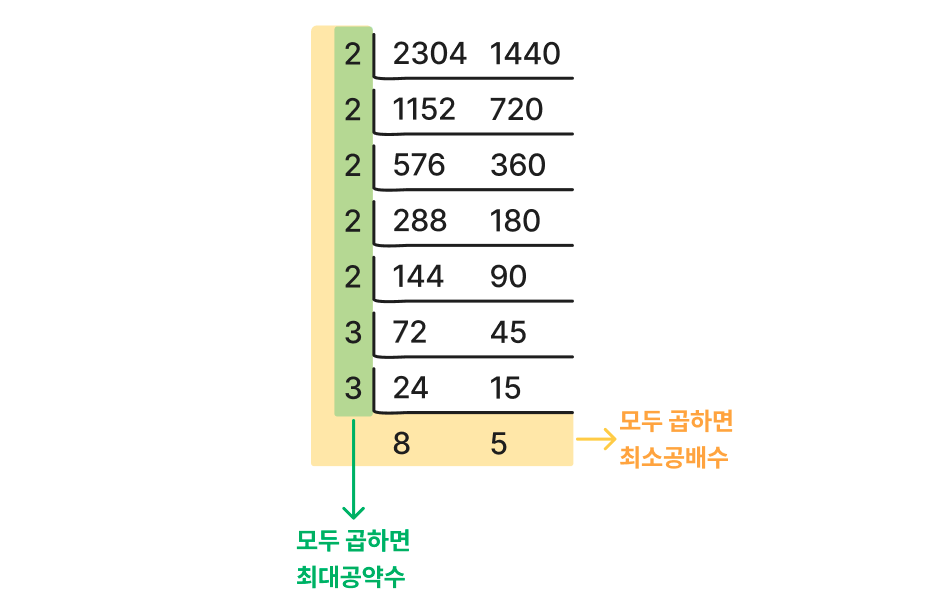
1. 나누는 수들을 모두 곱하면 288이 나오고 288이 최대 공약수다.
2. 최대공약수에 더이상 안나눠지는 밑 8, 5까지 다 곱하면 최소공배수가 나온다. (288 X 8 X 5)

유클리드 호제법

두 자연수의 최대공약수를 빠르게 구하는 알고리즘
시간 복잡도 : O(log N)

1. 큰 수(A)를 작은 수(B)로 나누기 (A > B면, A / B)
2. 나머지가 0이 아니면, 나누는 수(B)를 나머지(R)로 나눈다 (B / R)
3. 계속 반복해서 나머지가 0이면, 나누는 수가 최대공약수
   

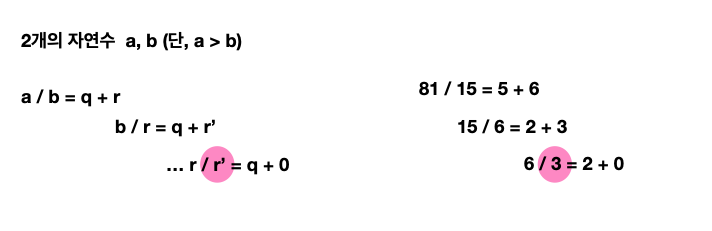
9/6 = 1 + 3
6/3 = 2 + 0
=> 나머지가 0일때 나누는 수 3이 최대공약수

최대공약수 GCD 구현방법

1. while 반복문으로 구현
   b가 0이 아니면 반복문실행, b가 0이면 a(이전반복에서의 a%b)반환

   function gcd(a, b){
       while(b !== 0){
           let r = a % b;
           a = b;
           b = r;
       } 
       return a;
   }

2. 재귀함수로 구현
   나머지가 있으면 재귀함수 실행, 나머지가 없으면 나누는 수가 최대공약수.

   const gcd = (a, b) => a % b ? gcd(b, a % b) : b;

최소공배수 LCM 구현

최소공배수 * 최대공약수 = a * b 이 공식 이용해 밑처럼 구현하기
최소공배수 = a * b / 최대공약수

const lcm = (a, b) => a * b / gcd(a, b);