Variance

• 분산은, 데이터가 얼마나 퍼져있는지를 측정하는 방법
• 각 값들의 평균으로부터 차이의 제곱 평균
  $v = \frac{\sum{(X_{i} - \overline{X})^{2}} }{N}$
  • $\overline{X}$ 는 평균, $N$ 은 관측의 수
  • $v$ 혹은 분산은 일반적으로 소문자 v로 표기되며 필요에 따라 $\sigma^{2}$로 표기
• 모집단의 분산 $\sigma^{2}$ 는 모집단의 PARAMETER
• 샘플의 분산 s2 는 샘플의 STATISTIC

Standard Deviation

• 표준편차는 분산의 값에 $\sqrt()$를 씌운 것

Covariance

• 1개의 변수 값이 변화할 때 다른 변수가 어떠한 연관성을 나타내며 변하는지를 측정하는 것
  

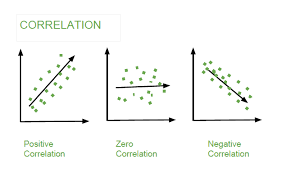
Correlation coefficient

• 공분산을 두 변수의 표준편차로 각각 나눠주면 스케일을 조정할 수 있으며 상관계수라고 부름
• 상관계수는 -1에서 1까지로 정해진 범위 안의 값만을 갖으며 선형연관성이 없는 경우 0에 근접하게 됨
  $cor(X,Y) = r = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}$

단위 벡터 (Unit Vectors)

• 선형대수에서 단위 벡터란 "단위 길이(1)"를 갖는 모든 벡터
  $v$ = [1, 2, 2]

||$v$|| = $\sqrt{1^2 + 2^2 + 2^2}$ = 3
$\hat{v}$ = 1 / ||$v$|| $\cdot$ $v$
= $1 \over 3$ $\cdot$ [1, 2, 2] = [$1 \over 3$, $2 \over 3$, $2 \over 3$]
||$\hat{v}$|| = 1

Span

• Span 이란 주어진 두 벡터의 (합이나 차와 같은) 조합으로 만들 수 있는 모든 가능한 벡터의 집합
• 주어진 두 벡터의 조합으로 만들 수 있는 공간

Basis

• 벡터 공간의 기저 (벡터)는 전체 공간을 span하는 선형적으로 독립적인 벡터의 집합

Rank

• 임의의 행렬 A가 있을 때 이 행렬의 Rank 라는 것은 이 행렬의 열들로 생성될 수 있는 벡터 공간의 차원을 의미

가우시안 소거법

• 사다리꼴 행렬을 만들어서 푸는것

projection

• 3차원 입체에서 2차원 평면 2차원 평면에서 1차원 직선 직선에서 다른 직선 등으로 도형을 변환시키는 것을 의미