[leetcode] Add One Row to Tree

문제

• 문제 링크
• 이진 트리 root와 두 정수 val, depth가 주어진다. tree의 depth 위치에 val 값을 갖는 노드를 추가해야 한다. root는 depth가 1이다.
• 노드를 추가할 때는 아래 규칙을 따른다.
  • 트리의 depth-1에 있는 null이 아닌 노드를 cur라고 한다면, val 값을 갖는 노드 두개를 각각 cur의 왼쪽, 오른쪽 자식 노드로 추가해야 한다.
  • 기존에 있던 cur의 왼쪽 자식 노드는 새로 추가된 노드의 왼쪽 자식 노드로 들어가야 한다.
  • 기존에 있던 cur의 오른쪽 자식 노드는 새로 추가된 노드의 오른쪽 자식 노드로 들어가야 한다.
  • 만약 depth가 1로 주어지면 val 값을 갖는 노드를 만들고, 왼쪽 자식 노드가 root인 노드를 반환한다.
• 제약 조건
  • 트리에 있는 노드 개수: [1, 10^4]
  • 트리의 깊이: [1, 10^4]
  • 노드 값 범위: -100 <= Node.val <= 100
  • 주어지는 val 범위: -10^5 <= val <= 10^5
  • 주어지는 depth 범위: 1 <= depth <= the depth of tree + 1
• 예시
  

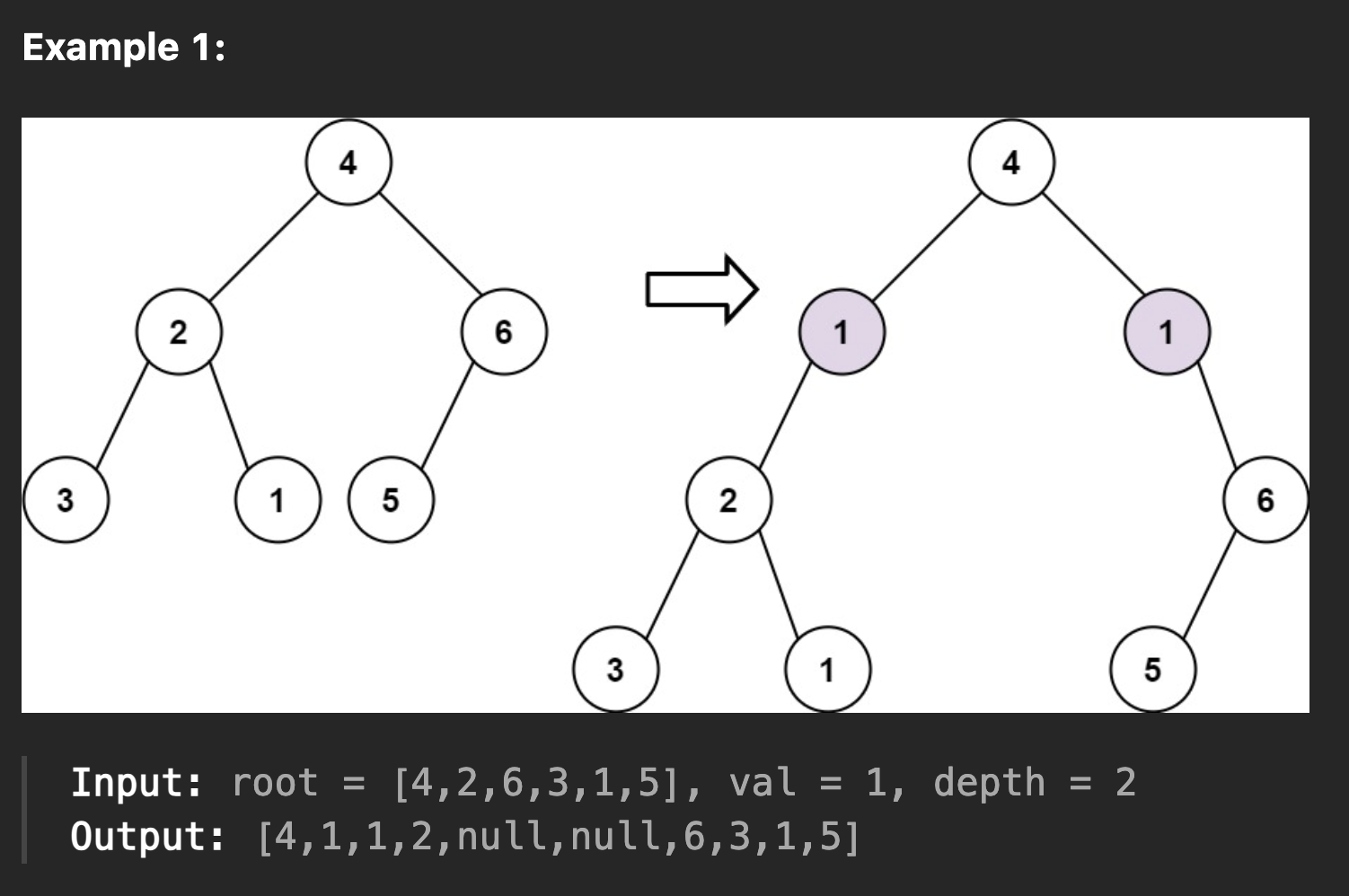
풀이

풀기 전

• 트리를 탐색하다가 특정 깊이에 도착했을 때, 규칙에 맞게 새로운 노드를 껴넣으면 된다.
• 주어진 예시에서는 노드가 두 개만 추가되고 있어서 헷갈릴 수 있는데, depth-1에 있는 모든 노드에 새로운 자식 노드를 추가해야 한다. 주어진 이진 트리가 꽉 차있는 트리(perfect binary tree)라면 추가되는 노드 개수는 2^(depth-1)개이다.

코드

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private void traverse(TreeNode node, int val, int nowDepth, int targetDepth) {
        if (node == null)
            return;

		// 현재 깊이에 1을 더한 값이 목표 깊이인지 확인한다.
        // 목표 깊이에 노드를 껴넣어야 하기 때문이다.
        if (nowDepth + 1 == targetDepth) {
        	// 현재 노드의 왼쪽 자식 노드를 왼쪽 자식 노드로 갖는 노드를 만든다. 그리고 만든 노드를 현재 노드의 왼쪽 자식 노드로 넣는다.
            node.left = new TreeNode(val, node.left, null);
            // 오른쪽도 동일하다.
            node.right = new TreeNode(val, null, node.right);
            return;
        }

		// 현재 노드의 왼쪽, 오른쪽 자식 노드를 탐색 - DFS
        traverse(node.left, val, nowDepth+1, targetDepth);
        traverse(node.right, val, nowDepth+1, targetDepth);
    }
    public TreeNode addOneRow(TreeNode root, int val, int depth) {
    	// depth가 1이면 root를 왼쪽 자식 노드로 갖는 새로운 트리를 반환한다.
        if (depth == 1)
            return new TreeNode(val, root, null);
        
        traverse(root, val, 1, depth);
        return root;
    }
}

푼 후

• 이전 문제들과 비슷하게 탐색하면서 조건에 맞게 풀면 된다.
• 최대 노드 개수만큼 탐색하므로 트리에 있는 총 노드 개수를 n이라고 하면 시간 복잡도는 O(n)이다. 재귀 함수를 최대 n개만큼 들어갈 수 있으므로 공간 복잡도도 O(n)이다.