문제
- 문제 링크
- 트리가 있을 때, 노드의 개수를 나타내는 정수 n과 노드의 연결 관계를 나타내는 이차원 배열 edges가 주어진다. 각 노드는 0~n-1의 라벨을 갖는다. 트리의 root를 임의로 정할 수 있는데, 특정 노드를 root로 정했을 때 트리는 높이 h를 갖는다. 가능한 모든 트리 중에서 가장 낮은 높이를 갖는 트리들을 MHT(Minimum Height Trees)라고 한다. MHT의 모든 root 라벨을 구해야 한다.
- 제약 조건
- 노드 개수:
1 <= n <= 2 * 10^4 - edges 길이:
edges.length == n - 1 - 주어진 값들은 tree임을 보장한다.
- 노드 개수:
- 예시
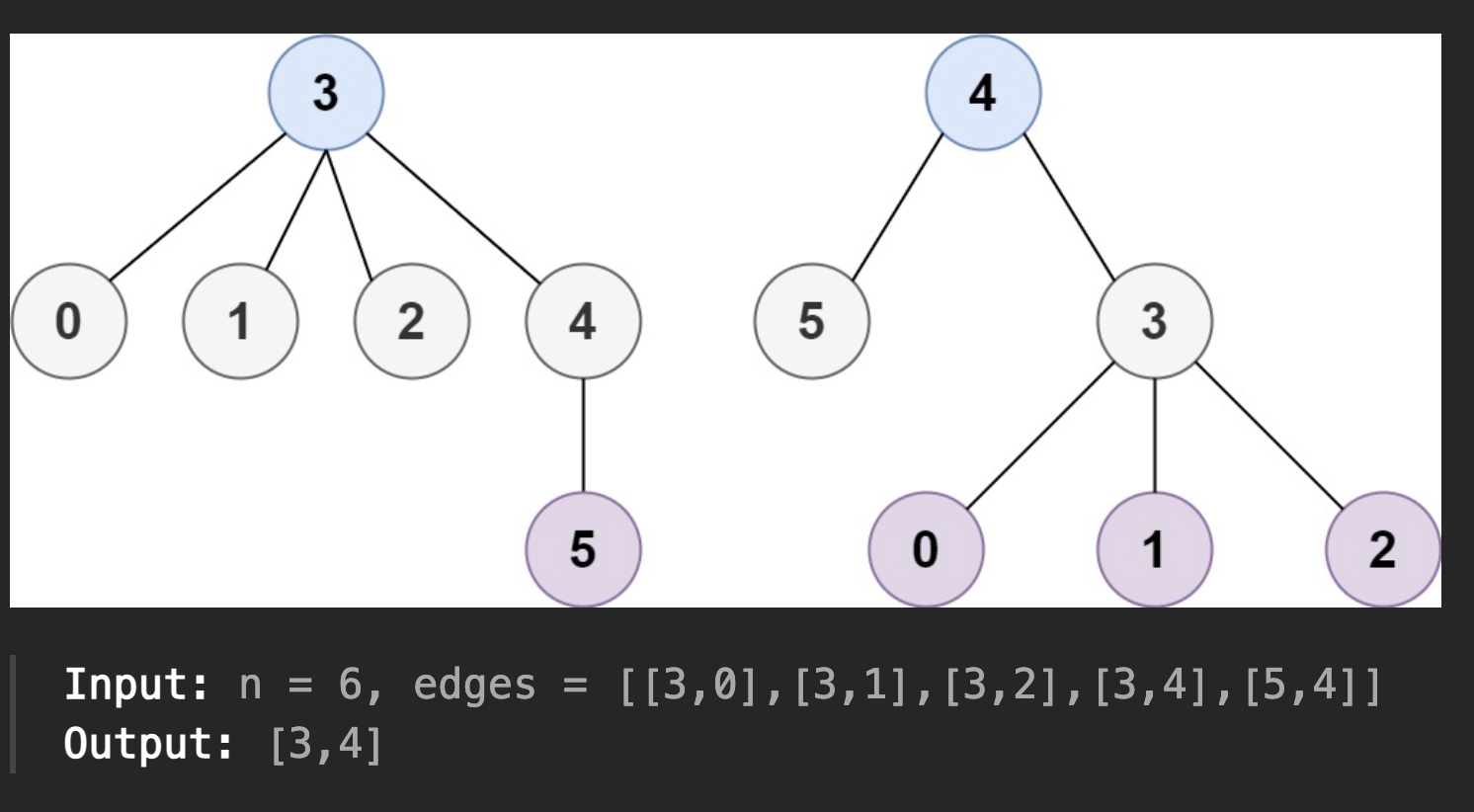
풀이
1. 끝 지점 찾고 중간 지점 찾기
풀기 전
- 중간 지점을 찾기 위해 우선 가장 긴 h를 찾은 뒤 2로 나눠야 될 거 같았다. 그래서 우선 가장 긴 H를 찾아야 했는데, 우선 임의의 노드에서 가장 먼 노드 A를 찾고, 찾은 노드에서 다시 가장 먼 B 노드를 찾으면 H를 구할 수 있었다.
- 다음은 중간 지점을 찾아야 했다.
- H가 짝수일 땐 A 노드에서부터 h/2 떨어진 노드를 찾으면 된다.
- H가 홀수일 땐 A 노드에서부터 h/2 떨어진 노드와 h/2+1 떨어진 노드를 찾으면 된다. B 노드 입장에서는 h/2+1 떨어진 노드와 h/2 떨어진 노드를 찾는 거였다.
- 그런데 간과했던 점은, A 노드에서 h/2+1만큼 떨어졌다고 B 노드에서 h/2만큼 떨어졌다는 보장이 없다는 것이다. 그래서 B 노드에서도 위 조건에 따라 중간 노드를 찾은 후, A 노드에서 구한 것과 겹치는 노드를 다시 구해줬다.
- 코드가 꽤.. 길어졌다.
코드
class Solution {
// 노드 연결
private void connect(List<List<Integer>> nodes, int[][] edges) {
int n1, n2;
for (int[] edge : edges) {
n1 = edge[0];
n2 = edge[1];
nodes.get(n1).add(n2);
nodes.get(n2).add(n1);
}
}
// 주어진 start 노드에서 가장 먼 노드와 거리를 반환한다.
private int[] findFarNode(List<List<Integer>> nodes, int start) {
Queue<Integer> q = new LinkedList<>();
boolean[] visited = new boolean[nodes.size()];
q.add(start);
visited[start] = true;
int maxRoot = 0;
int maxDepth = 0;
int depth = 1;
while (!q.isEmpty()) {
int size = q.size();
for (int i=0; i<size; i++) {
int now = q.poll();
for (int next : nodes.get(now)) {
if (visited[next])
continue;
q.add(next);
visited[next] = true;
// 가장 먼 노드와 거리를 찾는다.
if (depth > maxDepth) {
maxRoot = next;
maxDepth = depth;
}
}
}
depth++;
}
return new int[]{maxRoot, maxDepth};
}
// 주어진 root와 maxHeight를 사용해서 중간 지점에 있을 수 있는 노드를 찾는다.
private Set<Integer> findMinHeight(List<List<Integer>> nodes, int root, int maxHeight) {
Set<Integer> ret = new HashSet<>();
// 중간 지점에 있는 노드와의 거리이다.
List<Integer> targets = new ArrayList<>();
targets.add(maxHeight / 2);
if (maxHeight % 2 != 0)
targets.add(maxHeight / 2 + 1);
Queue<Integer> q = new LinkedList<>();
boolean[] visited = new boolean[nodes.size()];
q.add(root);
visited[root] = true;
int depth = 1;
while (!q.isEmpty()) {
int size = q.size();
for (int i=0; i<size; i++) {
int now = q.poll();
for (int next : nodes.get(now)) {
if (visited[next])
continue;
q.add(next);
visited[next] = true;
// 중간 지점을 찾으면 ret에 담는다.
if (targets.contains(depth))
ret.add(next);
// 중간 지점을 넘어가면 끝낸다.
else if (targets.get(targets.size() - 1) < depth)
return ret;
}
}
depth++;
}
return ret;
}
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1 || n == 2) {
List<Integer> ret = new ArrayList<>();
for (int i=0; i<n; i++)
ret.add(i);
return ret;
}
List<List<Integer>> nodes = new ArrayList<>(n);
for (int i=0; i<n; i++)
nodes.add(new ArrayList<>());
connect(nodes, edges);
int[] nodeInfo1 = findFarNode(nodes, 0); // 임의의 0번 노드로부터 가장 먼 노드를 찾는다.
int[] nodeInfo2 = findFarNode(nodes, nodeInfo1[0]); // 끝 노드 하나를 찾았으나, 가장 먼 반대편 노드를 찾는다.
int maxHeight = nodeInfo2[1]; // 트리에서 가장 긴 거리이다.
// 양끝 노드에서부터 중간 지점이 될 수 있는 후보 노드를 추린다.
Set<Integer> candi1 = findMinHeight(nodes, nodeInfo1[0], maxHeight);
Set<Integer> candi2 = findMinHeight(nodes, nodeInfo2[0], maxHeight);
// 후보 노드 중에서 겹치는 노드를 찾고 반환한다.
List<Integer> ret = new ArrayList<>();
for (int node : candi1) {
if (candi2.contains(node))
ret.add(node);
}
return ret;
}
}푼 후
- 더 쉬운 방법이 있을 거 같긴 했는데 생각이 안 났다. 그래도 힌트를 참고하기 전에 어떻게든 풀어보고 싶었다. 그래서 아주 긴 코드가 탄생했다.. discussion 글에서 제일 웃겼던 건
면접관이 이 문제를 낸다면 당신을 고용하기 싫다는 의미이다라고 적힌 거였다. 근데 반대로 면접에서 이런 문제가 나오면 그 회사에 가기 싫을 거 같다는 생각도 했다. - BFS를 네번 실행하기 때문에
시간 복잡도는 O(n)이다. 노드 연결 관계를 표현하기 위해 연결된 노드를 저장하므로, 간선 개수를 e라고 하면공간 복잡도는 O(n + e)다.
2. 칸 알고리즘 (Kahn's algorithm)
풀기 전
- 다른 사람들이 푸는 방식을 보니 칸 알고리즘을 사용했다고 한다. 위상 정렬에서 사용하는 알고리즘이라고 하는데 처음 들어본 거 같다. 들어봤는데 잊어버린 걸 수도..
- 알고리즘 자체는 간단했다. 우선 in-degree(노드로 들어오는 간선 개수)가 0인 노드를 모두 지운다. 노드가 지워지면서 다시 in-degree가 0이 된 노드를 모두 찾아서 지운다. 이를 반복한다. 지운 순서대로 나열하면 위상 정렬이 된다.
- 위 알고리즘을 해당 문제에 적용하면, in-degree가 0인 노드를 leaf 노드로 생각하면 된다. leaf 노드를 지우고, 다음 leaf 노드를 지운다. 그렇게 지우면 트리의 중간 지점을 찾을 수 있게 된다.
코드
class Solution {
private void connect(List<List<Integer>> nodes, int[][] edges) {
int n1, n2;
for (int[] edge : edges) {
n1 = edge[0];
n2 = edge[1];
nodes.get(n1).add(n2);
nodes.get(n2).add(n1);
}
}
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1 || n == 2) {
List<Integer> ret = new ArrayList<>();
for (int i=0; i<n; i++)
ret.add(i);
return ret;
}
List<List<Integer>> nodes = new ArrayList<>(n);
for (int i=0; i<n; i++)
nodes.add(new ArrayList<>());
// 노드 연결한다.
connect(nodes, edges);
// 연결된 간선 개수를 구한다.
int[] degreeNum = new int[n];
Queue<Integer> q = new LinkedList<>();
for (int i=0; i<n; i++) {
if (nodes.get(i).size() == 1) // leaf 노드이면 큐에 넣는다.
q.add(i);
else
degreeNum[i] = nodes.get(i).size();
}
int removed = 0;
// removed < n-2를 조건으로 주는 이유는, 중간 지점 노드가 최대 2개이기 때문이다.
while (removed < n - 2) {
int size = q.size();
for (int i=0; i<size; i++) {
int now = q.poll();
// 지운 leaf 노드와 연결된 노드의 간선 개수를 줄인다.
// 새롭게 leaf 노드가 된 것들을 큐에 넣는다.
for (int next : nodes.get(now)) {
degreeNum[next]--;
if (degreeNum[next] == 1)
q.add(next);
}
}
removed += size;
}
// 큐에 남아있는 노드가 중간 지점 노드이다.
List<Integer> ret = new ArrayList<>();
while (!q.isEmpty())
ret.add(q.poll());
return ret;
}
}푼 후
- 알고리즘을 보고 나니 간단하게 풀렸다. 코드 줄도 반으로 줄었다.
- 간선 개수가 1인지 확인하기 위해 연결된 노드를 모두 확인해야 해서 느려지지 않을까 싶었는데, 생각해보니 특정 노드 입장에서 leaf인지 확인되는 건 연결된 간선 개수만큼만 진행되기 때문에
시간 복잡도는 O(n + e)로 볼 수 있다.공간 복잡도도 O(n + e)다.
개발 일지