[leetcode] Number of Wonderful Substrings

문제

• 문제 링크
• 설명
  • 문자열 word가 주어진다. 최대 한 문자가 홀수번 포함되는 문자열을 wonderful string이라고 한다. word의 substring 중에서 wonderful string 개수를 구해야 한다.
    
• 제약 조건
  • word 길이: 1 <= word.length <= 10^5
  • word에는 'a'부터 'j'까지의 소문자만 들어간다.
• 예시
  

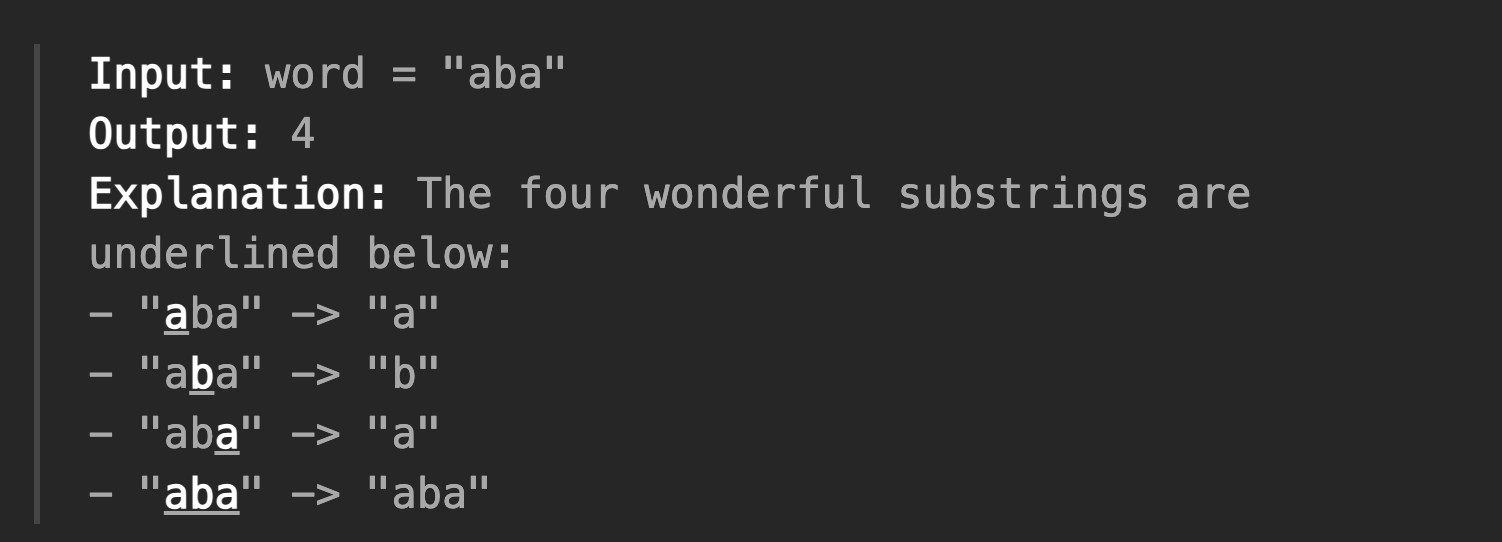
풀이

풀기 전

• medium이래서 방심했다가 결국 다른 풀이를 참고했다. 처음에 문제 자체도 이해가 되지 않았다. wonderful string을 다시 정의하면 문자열에 있는 문자가 모두 짝수개로 들어있거나, 하나만 홀수개로 들어있는 문자열이다.
• word의 최대 길이를 봤을 때 모든 substring을 순회할 수는 없었다. 힌트를 보니 비트 연산을 해야하는 거 같았는데, 문자 범위가 'a'~'j'로 10개뿐이라 각 문자의 빈도를 비트로 나타낼 수 있을 거 같았다. 그런데 이 이상 풀이가 떠오르지 않아서 다른 사람의 풀이를 열어버렸다.
• 참고한 풀이
  • 비트마스크 의미 정의
    • 문자 'a'를 0으로 놓으면, 'a'를 처음 만났을 때의 비트마스크를 1로 표현할 수 있다. 그리고 다시 'a'를 만났을 때 기존 비트마스크와 xor 연산을 하면 비트마스크는 0이 된다. 'a'가 홀수번 나왔는지 짝수번 나왔는지 알 수 있다.
      • 처음: 0 ^ (1 << 0) => 1
      • 두번째: 1 ^ (1 << 0) => 0
    • 문자 범위가 'a'~'j'로 10개뿐이므로, 비트마스크의 각 비트에 대응해서 사용하면 된다. 예를 들면 'b'가 홀수번 나왔으면 10으로 표현되고, 'c'는 100으로 표현된다. 'j'는 1000000000이다. 만약 'a'와 'j'만 홀수번 나왔으면 비트마스크는 1000000001로 표현된다. 비트마스크가 가질 수 있는 모든 경우의 수가 2^10이므로 총 1024개이다.
  • 비트마스크 활용
    • word에 있는 문자를 순회하면서, 문자를 비트마스크에 xor 연산한다. 만약 계산된 비트마스크가 이전에 나온적이 있다면, 그만큼 정답에 더해준다. 왜냐하면 이전에 해당 비트마스크가 나왔던 문자 이후부터 현재 문자까지 wonderful string임을 의미하기 때문이다. 만약 'abaa'라는 문자가 있으면 비트마스크는 1 -> 11 -> 10 -> 11 순서로 변한다. 이때 11이 두번 나오는데, 처음 나온 11은 'ab'이고 두번째는 'abaa'이다. 'abaa'에서 'ab'를 뺀 'aa'가 wonderful string임을 알 수 있다. 이렇게 되는 이유는, 비트마스크가 같다는 건 두 문자 사이에 다른 문자들이 없었거나 짝수개로 등장했다는 걸 의미하기 때문이다.
    • 그 다음에는 마스크비트의 각 비트마다 flip 해주며, 이전에 나온적이 있는 빈도만큼 정답에 더해준다. 문제에서 최대 1개만큼 홀수개 문자를 허용하기 때문이다.

코드

class Solution {
    public long wonderfulSubstrings(String word) {
        long[] cnt = new long[1024];  // 비트마스크의 빈도를 저장한다.
        cnt[0] = 1;  // 비트마스크가 0인 빈 문자열을 포함해준다.
        
        long ret = 0;
        int mask = 0;  // 비트마스크
        for (char ch : word.toCharArray()) {
            int idx = ch - 'a';  // 문자를 숫자로 변환한다.
            
            // 문자에 따라 비트를 따로 쓰도록 shift 해주고, xor 연산을 한다.
            // 각 비트는 문자가 홀수개로 나왔는지 짝수개로 나왔는지 의미한다.
            mask ^= 1 << idx;
            
            // 이전에 나왔던 비트마스크 빈도만큼 정답에 더해준다.
            ret += cnt[mask];
            
            // 문자 하나까지는 홀수개여도 되므로 이때 빈도수를 구해준다.
            for (int i=0; i<10; i++) {
                ret += cnt[mask ^ (1 << i)];
            }
            
            // 현재 비트마스크의 빈도를 더해준다.
            cnt[mask]++;
        }
        return ret;
    }
}

푼 후

• word를 한 번 순회하므로 시간 복잡도는 O(word.length)이다. 상수 공간만 추가되기 때문에 공간 복잡도는 O(1)이다.
• 비트 연산에 취약한 것도 있는데 풀이를 떠올리기 어려워서 객관적으로도 어려운 문제인 거 같다. 이해한 거 같으면서도 막상 설명하려면 어렵다. 제대로 이해가 안 됐다는 의미다.