[leetcode] Sum of Distances in Tree

문제

• 문제 링크
• n개의 노드를 가진 무방향 트리가 있다. 정수 n과 노드의 연결 관계를 나타내는 이차원 배열 edges가 주어진다. 노드는 0~n-1로 라벨링 되어있다. 배열 answer를 반환해야 하는데, answer[i]는 i번째 노드에서부터 그 외 모든 노드까지 거리를 모두 더한 값이다.
• 제약 조건
  • n의 범위: 1 <= n <= 3 * 10^4
  • edges 길이: edges.length == n - 1
• 예제
  

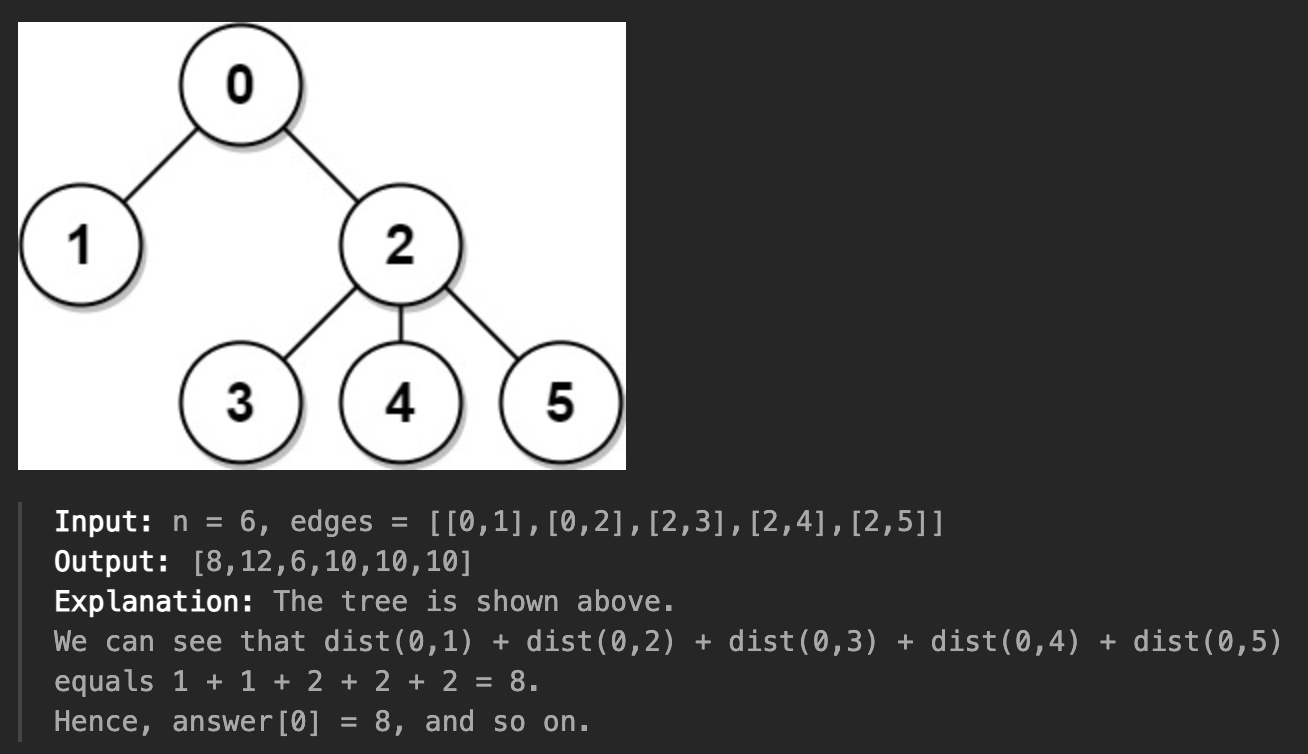
풀이

풀기 전

• 풀다가 안 되겠어서 풀이를 봤다ㅎ
• 실패한 방법
  • 주어진 제약 조건으로는 O(n)의 시간 복잡도를 가져야 한다. i번째 노드 입장에서 직접적으로 연결된 노드에 저장된 값만으로 answer[i]를 도출할 수 있어야 한다는 것이다. 일단 규칙을 찾아봐야 했다. 만약 노드 i에 연결된 노드 j가 있다면, answer[i->j] + (j 이후로 연결된 노드 개수 + 1)라는 식을 찾을 수 있었다. 해당 식이 의미하는 건, 아래와 같다.
    • answer[i->j]: 노드 i를 부모 노드로 가질 때, 노드 j 입장에서 모든 자식 노드까지의 거리 합이다.
    • (j 이후로 연결된 노드 개수 + 1): 노드 i와 노드 j를 잇는 간선을 노드 j의 자식 노드 개수만큼 더해주는 거다. 1을 추가로 더한 이유는 노드 j 자체도 더해줘야 하기 때문이다.
  • 위 규칙을 바탕으로 이차원 배열을 만들어서 풀어보려 했지만 메모리 초과가 났다ㅎ 다른 방법은 더 생각이 안 나서 풀이를 찾아봤다. 식을 세우는 거 자체는 비슷했는데, 이차원 배열을 사용하지 않고 푸는 방식이었다.
• 참고한 풀이
  • 우선 임의의 노드를 root로 잡고 부모-자식 관계를 갖는 트리를 만든다.
  • 모든 노드에서 자식 노드의 개수와 모든 자식 노드까지의 거리 합을 구한다.
    • 자식 노드 개수: cnt[parent] = cnt[child] + 1
    • 자식 거리 합: sum[parent] = sum[child] + cnt[child] + 1
  • 자식이 아닌 노드에 대해서도 거리의 합을 구해준다.

    • child_cnt = cnt[child] + 1;
      sum[child] = sum[parent] - child_cnt + (n - child_cnt);

    • child_cnt를 빼주는 이유는 parent와 child에 이어진 간선이 child의 자식 노드 개수만큼 sum[parent]에 더해져있기 때문이다. 우선 이걸 빼주는 작업이다.
    • 그 후 (n - child_cnt)를 더해주는 이유는 parent와 child에 이어진 간선을 아직 적용되지 않은 다른 노드만큼 추가해야 하기 때문이다. 부모 노드로부터 연결된 모든 노드 개수만큼 간선을 왔다갔다 한다고 생각하면 된다.
  • 위 작업을 거치면 sum[i]가 곧 answer[i]를 의미한다.

코드

class Solution {
	// node의 자식 노드 개수와 자식 노드들까지 거리의 합을 구한다.
    private void getSubCnt(int node, int parent, List<Integer>[] nodes, int[] subSum, int[] subCnt) {
        for (int child : nodes[node]) {
            if (child == parent)
                continue;

            getSubCnt(child, node, nodes, subSum, subCnt);
            subCnt[node] += subCnt[child] + 1;
            subSum[node] += subSum[child] + subCnt[child] + 1;
        }
    }

	// 자식 노드뿐만 아니라, 아직 적용하지 않은 부모 노드들까지의 거리 합도 구한다.
    private void getOtherSubSum(int node, int parent, List<Integer>[] nodes, int[] subSum, int[] subCnt) {
        for (int child : nodes[node]) {
            if (child == parent)
                continue;
        
            subSum[child] = subSum[node] - (subCnt[child] + 1) + (nodes.length - (subCnt[child] + 1));
            getOtherSubSum(child, node, nodes, subSum, subCnt);
        }
    }

    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        List<Integer>[] nodes = new List[n];
        for (int i=0; i<n; i++)
            nodes[i] = new ArrayList<>();

        int[] subCnt = new int[n];
        int[] subSum = new int[n];
        
        for (int[] edge : edges) {
            int node1 = edge[0];
            int node2 = edge[1];
            nodes[node1].add(node2);
            nodes[node2].add(node1);
        }

        getSubCnt(0, -1, nodes, subSum, subCnt);
        getOtherSubSum(0, -1, nodes, subSum, subCnt);
        
        int[] ret = new int[n];
        for (int i=0; i<n; i++)
            ret[i] = subSum[i];
        return ret;
    }
}

푼 후

• 노드 개수만큼 자식 노드 개수와 거리 합을 구하므로 시간 복잡도는 O(n)이다. 연결 관계를 나타내기 위해 사용하는 List 배열이 있으므로 공간 복잡도는 O(n + edges.length)이다.
• 최근 연속으로 DP 문제가 나왔는데 그 중에 제일 골치 아팠던 거 같다.. 메모리 초과 났던 방식으로 풀 때도 깔끔한 방법이 아닌거 같아서 찜찜했는데, 실제 풀이도 복잡한 편인 거 같다. 그래도 식을 비슷하게 세웠다는 거에 위안을 가져본다ㅎ