[leetcode] Trapping Rain Water

문제

• 문제 링크
• 각 막대의 너비가 1인 높이 지도를 나타내는 양의 정수 배열 height가 주어진다. 비가 온 후에 얼마의 물이 채워지는지 구해야 한다.
• 예시
  
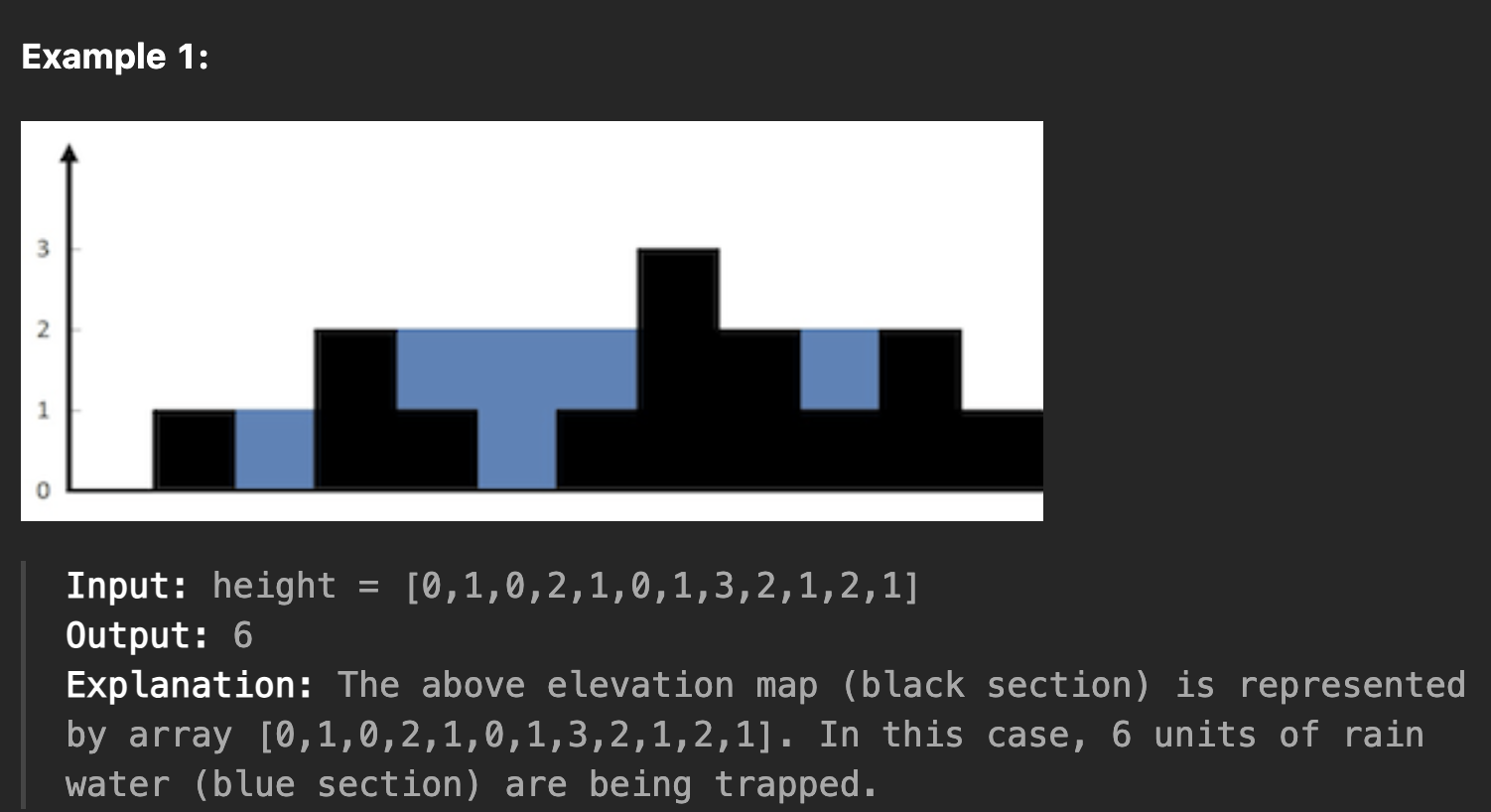
• 제약 조건
  • height 길이: 1 <= height.length <= 2 * 10^4
  • height 값 범위: 0 <= height[i] <= 10^5

풀이

풀기 전

• 규칙을 찾기 위해 예시로 이리저리 생각해봤다. 그러다 아래 규칙을 찾았다.
  • 현재 위치에서 다음 위치로 갈 때 고도가 낮아지는 경우
    • 현재 위치와 다음 위치 이후에 물이 고일 수 있다. 현재 위치를 저장해야 한다.
  • 현재 위치에서 다음 위치로 갈 때 고도가 높아지는 경우
    • 현재 위치에 물이 고일 수 있다. 현재 위치보다 고도가 높았던 이전 위치와 다음 위치 사이에 물이 고일 수 있기 때문이다. 저장해놨던 이전 위치를 꺼내서 물이 얼마나 찰 수 있는지 확인한다. 이전 위치는 여러 곳일 수 있다.
• 위 규칙을 구현하기 위해 아래처럼 코드 작성했다.
  • Block 클래스를 정의했다. 높이와 인덱스를 저장한다. 인덱스를 저장하는 이유는 물의 넓이를 구하기 위해서다.
  • height를 순회한다.
    • 다음 위치에서 고도가 낮아지는 경우, 현재 위치를 스택에 저장한다.
    • 다음 위치에서 고도가 높아지는 경우, 스택이 비어있지 않다면 물이 고일 수 있다는 의미이다. 스택에서 이전 위치를 꺼내서 물이 고일 수 있는 넓이를 구한다. 스택이 비거나 이전 위치의 높이가 다음 위치의 높이보다 높아질 때까지 반복한다.
  • 구한 물의 넓이를 반환한다.

코드

class Solution {
    private class Block {
        int height;
        int idx;  // 막대 간의 거리 구할 때 사용한다.

        public Block(int height, int idx) {
            this.height = height;
            this.idx = idx;
        }
    }

    public int trap(int[] height) {
        int ans = 0;
        Stack<Block> stack = new Stack<>();
        
        int minHeight = 0;
        for (int i=0; i<height.length - 1; i++) {
            int now = height[i];  // 현재 높이
            int next = height[i+1];  // 다음 높이
            
            if (now > next) {  // 고도가 낮아지면 스택에 넣는다.
                stack.push(new Block(now, i));
            } else {  // 고도가 높아지면 물이 고일 수 있는 곳을 확인한다.
                Block pre = null;
                minHeight = now;  // 처음에 가장 낮은 높이는 현재 높이다.
                while (!stack.isEmpty()) {
                    pre = stack.pop();  // 이전 위치를 꺼낸다.
                    int h = Math.min(pre.height, next);  // 이전 높이와 다음 높이 중 낮은 높이를 구한다. 물의 넓이 구할 때 사용한다.
                    ans += (h - minHeight) * (i - pre.idx);  // 물의 넓이 구한다.
                    minHeight = h;  // 다음 계산을 위해 가장 낮은 높이를 갱신한다.

					// 만약 이전 높이가 다음 높이보다 높다면 스택에 넣고 반복문 끝낸다.
                    // 다음 높이로 채울 수 있는 물은 다 채웠고, 이전 높이가 다시 쓰일 수 있기 때문이다.
                    if (pre.height > next) {
                        stack.push(pre);
                        break;
                    }
                }
            }
        }
        return ans;
    }
}

푼 후

• 좀 복잡하게 푼 거 같다. height를 한 번 순회하면서, 내부에서도 while의 시간 복잡도가 선형적으로 증가하기 때문에 시간 복잡도는 O(height.length)이다. stack는 height 길이만큼만 사용되므로 공간 복잡도도 O(height.length)이다.
• 다른 사람들이 푼 걸 보니 엄청 간단하게 풀었다. 설명하면 아래와 같다.
  • height와 같은 길이의 left 배열을 만든 뒤, height를 왼쪽에서 오른쪽으로 순회하며 현재까지 만난 값 중에 max 값을 각 인덱스에 저장한다.
  • 다시 같은 길이의 right 배열을 만든 뒤, height를 오른쪽에서 왼쪽으로 순회하며 현재까지 만난 값 중에 max 값을 각 인덱스에 저장한다.
  • 이때 min(left[i], right[i])가 의미하는 건 i 위치에서 왼쪽과 오른쪽으로부터 둘러쌓일 수 있는 높이를 의미한다. 만약 height[i] < min(left[i], right[i]) 이면, 그 차이만큼 물이 고일 수 있다는 의미이다.
  • 코드를 보고 어떻게 풀었는지 이해는 했지만 아이디어를 혼자 생각해내기는 어렵겠다는 생각을 했다. 특정 위치 하나에 집중해서 얼마나 고일 수 있는지 알아낸 느낌인데.. 어렵다 어려워. 무튼 이렇게 풀면 속도가 빠르긴 하다.