Path Tracking Algorithm
Pure Pursuit
설명
로봇의 현재 위치와 전방 주시 지점(look-ahead point)을 통해 조향각을 계산하고 차량의 해당 위치까지 이동시키는 제어 기법입니다. 차량이 목표 지점으로 이동할 때까지 전방 주시 지점이 변화합니다. LookAheadDistance를 통해 어느 정도 거리에 전방 주시 지점을 놓을지 결정할 수 있습니다. 또한, 이 알고리즘은 차량의 후륜 축의 중심을 기준점으로 계산됩니다.(GNSS를 통한 경로 추종 시 센서의 위치를 후륜 축의 중심으로 두는 게 좋습니다.)
전방 주시 거리(LookAheadDistance)
전방 주시 거리(look ahead distance)는 로봇의 조향각을 계산하기 위해 현재 위치에서 경로를 따라 얼마나 멀리 봐야 하는지를 나타냅니다. 이때 영향을 주는 정보는 차량의 속도 및 차량의 규격 등이 있습니다. 아래 그림은 로봇과 전방 주시 지점을 보여줍니다. 이 이미지에 표시된 것처럼 실제 경로는 웨이포인트 사이의 직선과 일치하지 않습니다.
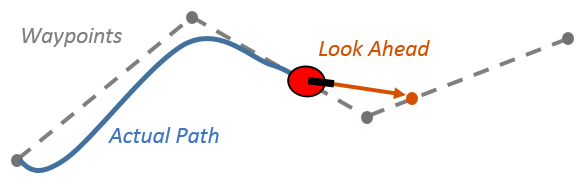
LookAheadDistance을 작게 설정하며 로봇이 경로를 향해 빠르게 이동합니다. 그러나 다음 그림에서 볼 수 있듯이 로봇은 경로를 벗어나면서 목표 경로를 따라 진동합니다. 경로를 따라 진동하는 것을 줄이기 위해 더 큰 값의 전방 주시 거리를 사용할 있지만, 그럴 경우 코너 근처에서 더 큰 곡률이 발생할 수 있습니다.
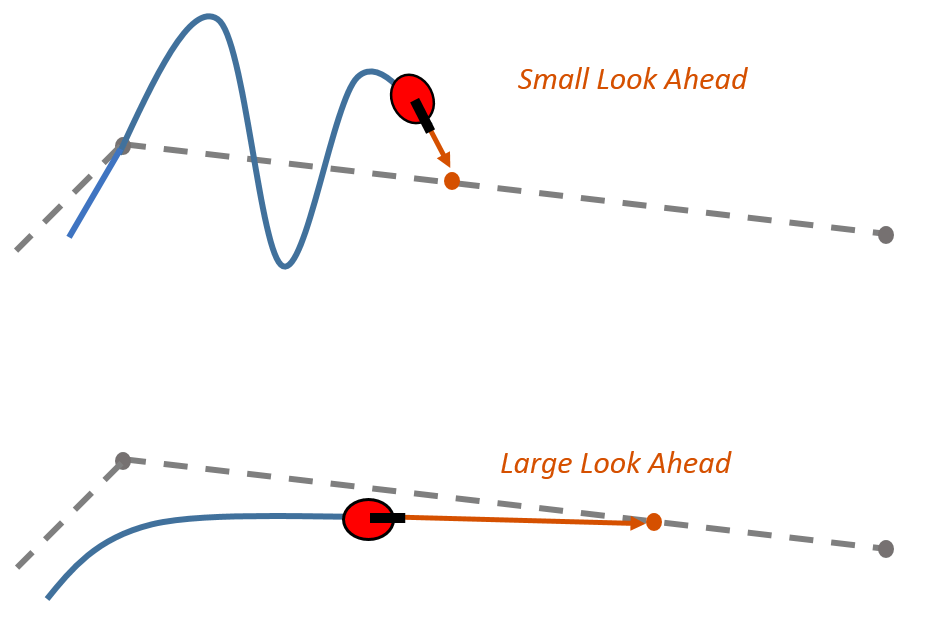
수식
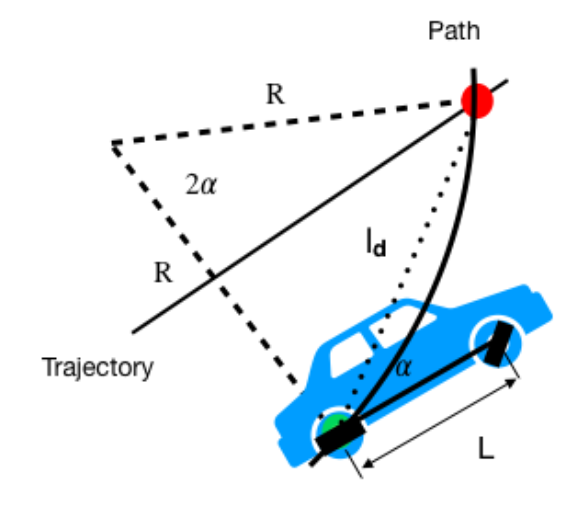
조향각은 아래와 같이 구할 수 있습니다.
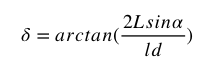
코드구현
for i in self.path.poses :
path_point=i.pose.position
dx= path_point.x - vehicle_position.x
dy= path_point.y - vehicle_position.y
rotated_point.x=cos(self.vehicle_yaw)*dx + sin(self.vehicle_yaw)*dy
rotated_point.y=sin(self.vehicle_yaw)*dx - cos(self.vehicle_yaw)*dy
if rotated_point.x>0 :
dis=sqrt(pow(rotated_point.x,2)+pow(rotated_point.y,2))
if dis>= self.lfd :
self.lfd=self.current_vel * 0.65
if self.lfd < self.min_lfd :
self.lfd=self.min_lfd
elif self.lfd > self.max_lfd :
self.lfd=self.max_lfd
self.forward_point=path_point
self.is_look_forward_point=True
break
alpha=atan2(rotated_point.y,rotated_point.x)현재 차량의 정보와 전체 경로 상의 위치를 통해 rotated_point의 x,y좌표 값을 결정합니다. 이때, rotated_point의 길이는 차량에서 목표지점까지의 거리를 나타내며, 이때의 각도는 목표지점까지의 방향에서 차량의 헤딩 방향까지의 각도입니다. 만약 rotated_point가 전방에 존재하고 그 길이가 전방 주시 거리 이상이면 그 값을 통해 위의 수식에서의 알파 값을 구해줍니다. 이때, 전방 주시 거리는 속도에 의해 변경 됩니다.
if self.is_look_forward_point :
self.steering=atan2((2*self.vehicle_length*sin(theta)),self.lfd)*180/pi #deg
return self.steering ## Steering 반환 ##
else :
print("no found forward point")
return 0구해진 알파 값을 통해 조향각을 계산합니다.
Stanley
설명
앞선 Pure Pursuit과 반대로 Stanley기법은 차량의 후륜축이 아닌 전방축을 기준으로 계산합니다. Stanley기법은 횡방향 오차와 차량과 경로 사이의 뱡향차이를 통해 조향각을 계산합니다. 이때, 횡방향 오차는 추종하고자 하는 경로와 차량의 전방축 사이의 거리입니다. 조향각은 횡방향 오차와 방향 차이가 0이 되도록 하는 계산됩니다.
수식
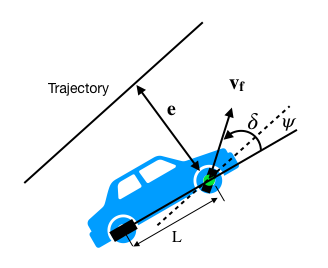
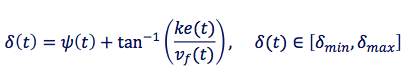
k는 조정 상수입니다. 값이 클수록 차량은 빠르게 경로를 따라 움직이지만 오실레이션의 위험이 있습니다.
코드구현
아래 출처 사이트의 코드를 인용하여 필요해 맞게 수정하였습니다.
from cmath import inf
import numpy as np
import matplotlib.pyplot as plt
dt = 0.1
k = 2 # control gain
L = 2
max_steering = np.radians(25) # max_angle = 25 degree
# map
ref_xs = np.linspace(0, 20, 100)
ref_ys = 0.1 * (ref_xs*ref_xs)
ref_yaws = np.arctan(np.gradient(ref_ys))
class VehicleModel(object):
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw*np.pi/180
self.v = v
def update(self, steer):
self.yaw += self.v / L * np.tan(steer) * dt # yaw(n+1) = yaw(n) + L * v * tan(steer) * dt
self.yaw = self.yaw % (2.0 * np.pi) # yaw = yaw % 2π
self.x += self.v * np.cos(self.yaw) * dt # x(n+1) = x(n) + v * cos(yaw) * dt
self.y += self.v * np.sin(self.yaw) * dt # y(n+1) = y(n) * v * sin(yaw) * dt
self.v = self.v # v(n+1) = v(n)
def normalize_angle(angle):
while angle > np.pi: # angle > π ----> angle = angle - 2π
angle -= 2.0 * np.pi # ex) 270 degree = -90 degree
while angle < -np.pi: # angle < π ----> angle = angle + 2π
angle += 2.0 * np.pi # ex) -270 degree = 90 degree
return angle
def stanley_control(x, y, yaw, v, ref_xs, ref_ys, ref_yaws):
# find nearest point
min_dist = 1e9
min_index = 0
n_points = len(ref_xs)
front_x = x + L * np.cos(yaw) # x = back wheel position
front_y = y + L * np.sin(yaw) # y = back wheel position
for i in range(n_points): # find x coordinate index
dx = front_x - ref_xs[i]
dy = front_y - ref_ys[i]
dist = np.sqrt(dx * dx + dy * dy)
if dist < min_dist:
min_dist = dist
min_index = i
# compute cte at front axle
ref_x = ref_xs[min_index]
ref_y = ref_ys[min_index]
ref_yaw = ref_yaws[min_index]
dx = ref_x - front_x
dy = ref_y - front_y
perp_vec = [np.cos(ref_yaw + np.pi/2), np.sin(ref_yaw + np.pi/2)]
cte1 = np.dot([dx, dy], perp_vec)
cte2 = np.sqrt(np.dot([dx, dy],[dx, dy]))
if ref_y < front_y:
cte2 *= -1
# control law
psi = normalize_angle(ref_yaw - yaw)
cte_term = np.arctan2(k*cte1, v)
# steering
steer = psi + cte_term
steer = np.clip(steer, -max_steering, max_steering) # limit the steering angle
return steer, ref_x, ref_y
# vehicle
model = VehicleModel(x=0.0, y=2.0, yaw=70, v=1.0)
steer = 0
xs, ys, yaws = [[], [], []]
steers = []
ts = []
dxs, dys = [], []
for step in range(200):
t = step * dt
steer, dx, dy = stanley_control(model.x, model.y, model.yaw, model.v, ref_xs, ref_ys, ref_yaws)
xs.append(model.x)
ys.append(model.y)
yaws.append(model.yaw)
ts.append(t)
steers.append(steer)
dxs.append(dx)
dys.append(dy)
model.update(steer)
# plot car
plt.figure(figsize=(12, 3))
plt.plot(ref_xs[:60], ref_ys[:60], 'r--', alpha=0.5, label="reference")
for i in range(len(xs)):
if i % 20 == 0:
plt.plot(xs, ys, 'b--', alpha=0.5)
plt.axis("equal")
plt.xlabel("X [m]")
plt.ylabel("Y [m]")
plt.legend(loc="best")
plt.tight_layout()
plt.savefig("stanley_method.png", dpi=300)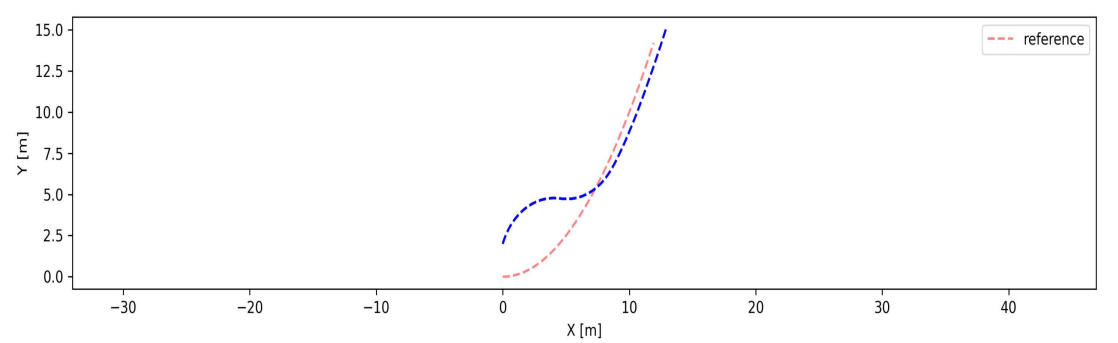
출처
https://kr.mathworks.com/help/nav/ug/pure-pursuit-controller.html
https://m.blog.naver.com/rich0812/222592223219
https://github.com/WeGo-Robotics
https://blog.naver.com/PostView.naver?blogId=rich0812&logNo=222598072957&categoryNo=20&parentCategoryNo=0
https://velog.io/@openjr/Stanley-method-%EC%B4%9D-%EC%A0%95%EB%A6%AC
