Begining of DeepLearning_XOR

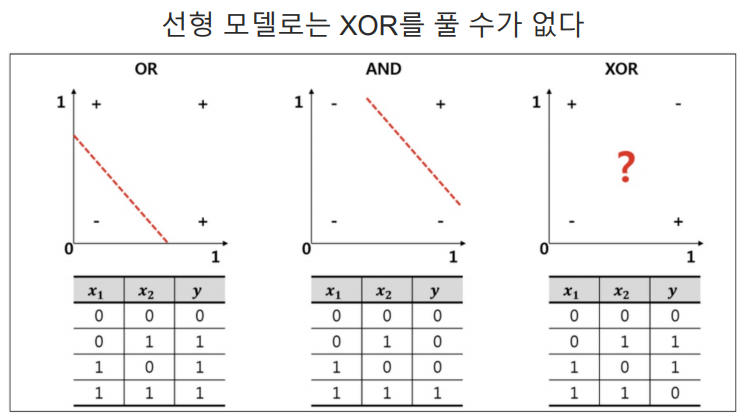
• 이번에는 분류문제인데, 단순 회귀직선이 아닌 여러 Layer를 통해 모델을 구축하는 모형을 만들어봤다.
• 앞에 or, and의 경우 하나의 직선을 통해 모델을 구축할 수 있지만, XOR의 경우 두 개의 직선 혹은 비선형 회귀직선이 필요하다.
• 여러 층의 Layer를 사용할 때 큰 문제는 중간 Layer 학습과정에서 어떤 값을 정답으로 입력하냐가 문제인데, 이 문제를 backpropagation방식으로 해결했다.
• 위 방법은 정말 단순하게 그냥 역순으로 loss값의 편미분값을 통해 값을 도출해간다.
  
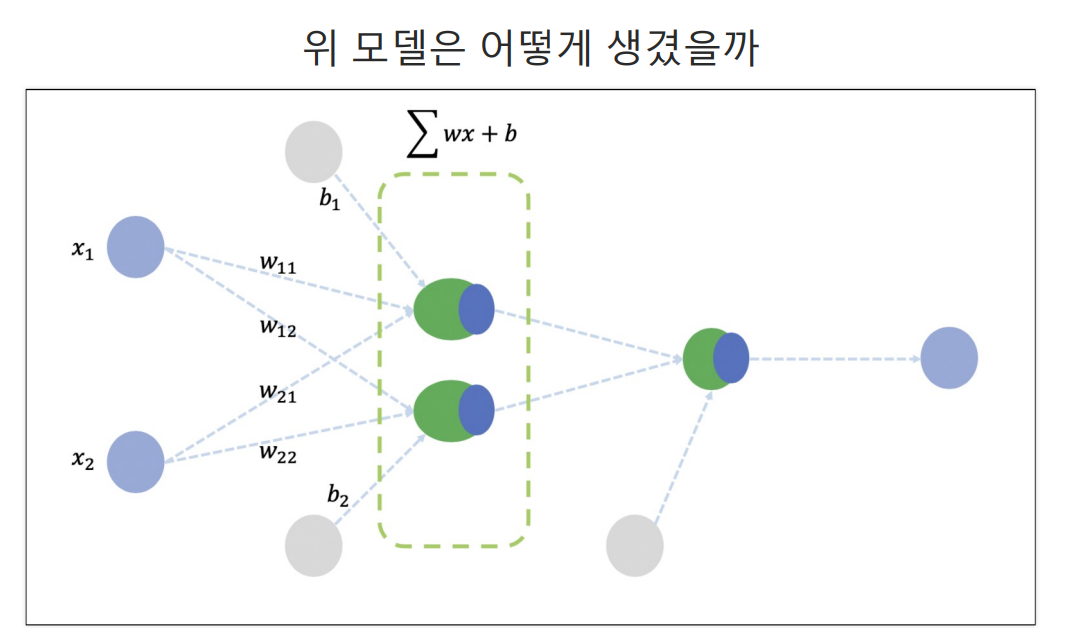
• 위 초록색 두 Layer에서 backpropagation방식을 통해 loss값을 계산하고, 결과를 도출한다.
  
• 이렇게 여러 층의 레이러를 통해 위 모델을 구축했다.
• activation에 sigmoid를 사용한 이유는 결국 두 개의 선이 다 직선일 경우 최종 결과도 직선이기 때문에 sigmoid를 통해 비선형 회귀직선을 구현했다.
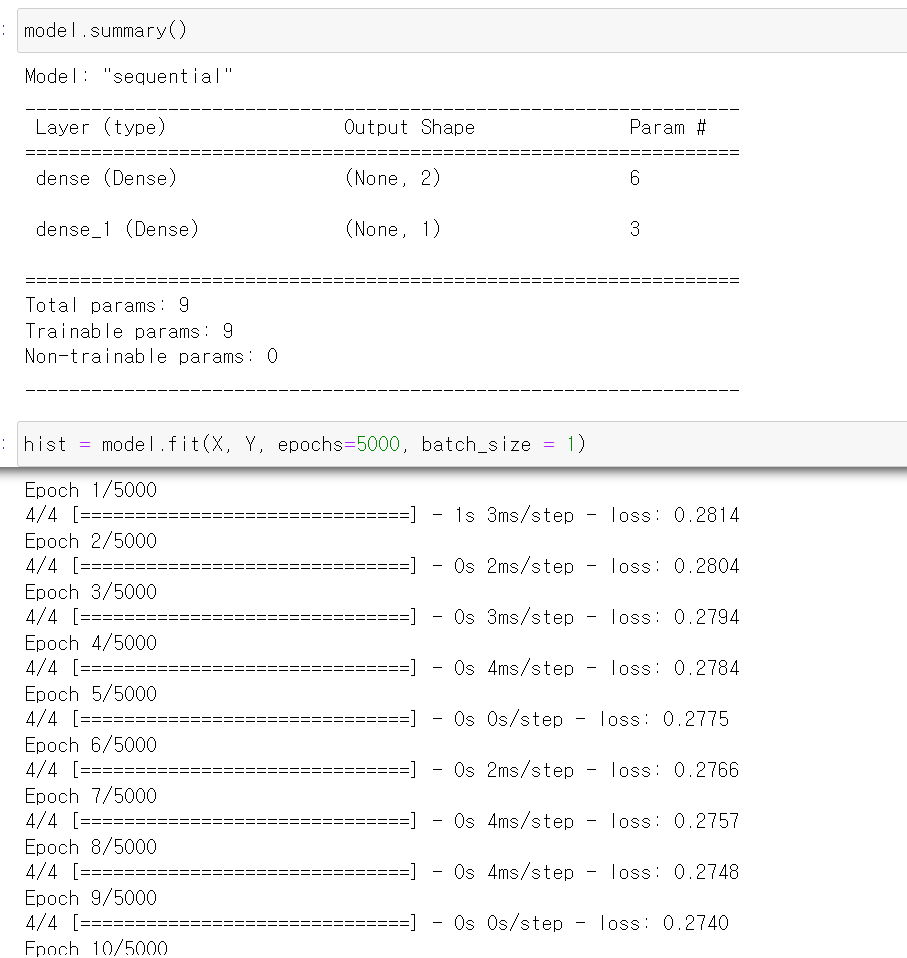
• 해당 모델을 통해 5000의 epoch를 통해 학습시킨 결과
  
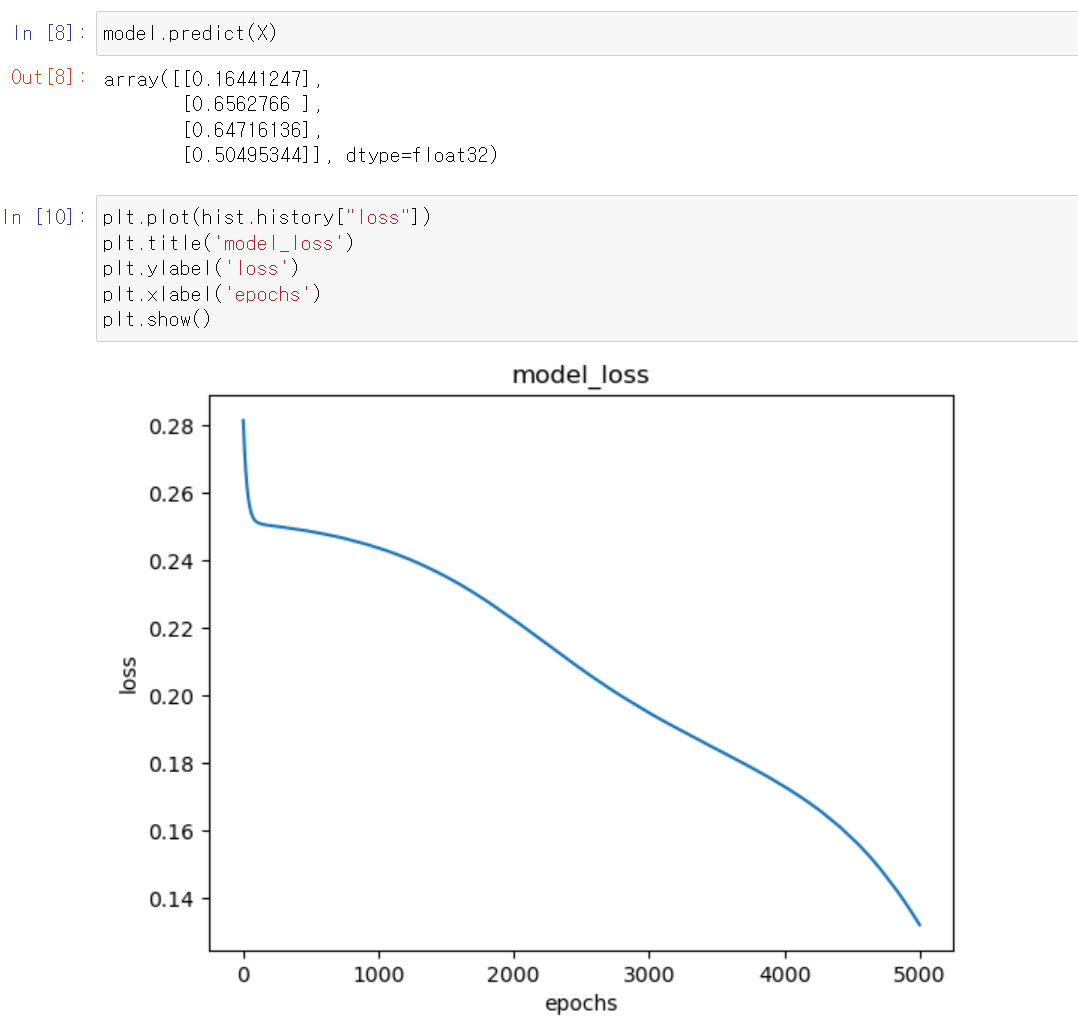
• loss값이 점점 더 떨어지는 것을 볼 수 있다.
  
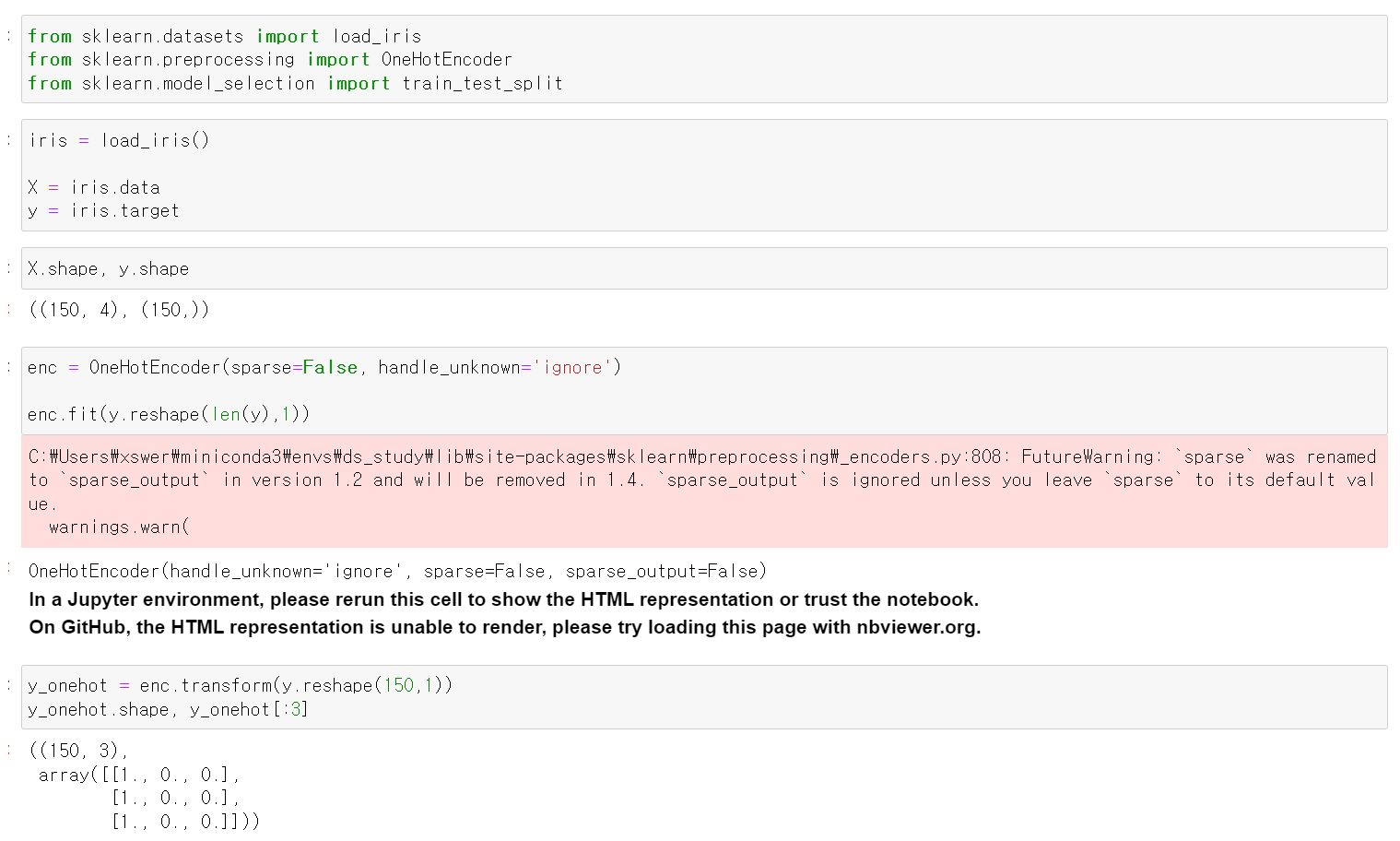
• 이제 위 방법을 통해 iris 데이터로 딥러닝 모델을 구축해봤다.
• 먼저 iris데이터를 불러오고, x와 y데이터의 shape을 확인 후 y데이터의 shape를 (150, 1) 변환 후 OnehotEncorder로 바꿨다.
• OneHotEncorder를 사용하는 이유는

예측값 0 - 실제값 0 = 0
예측값 0 - 실제값 2 = -2
이렇게 예측이 틀렸다는 결과는 같은데 error값이 달라지기 때문에 해당 문제를 해결하기 위해
OneHotEncorder방법을 사용한다.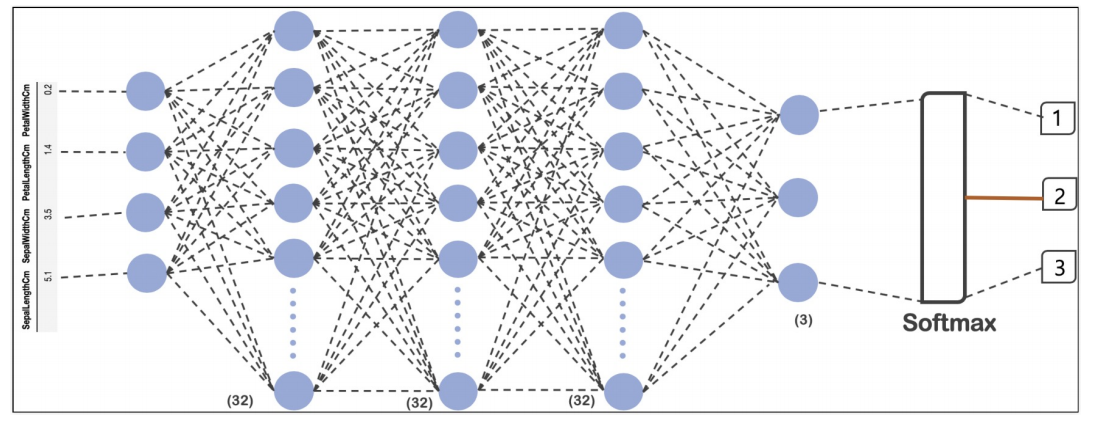

• 이제 위 모델과 같이 구현하기 위해 Layer를 구축했다.
  
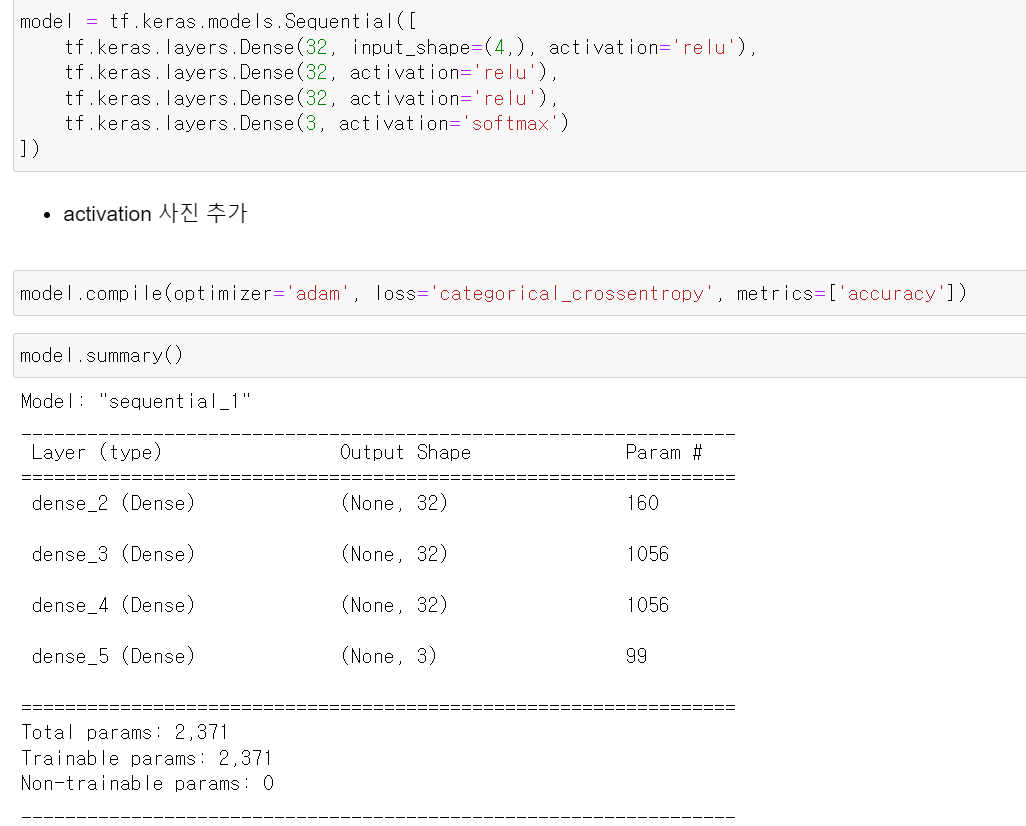
• Dense를 통해 여러 층의 Layer를 구축하고, activation은 relu로 입력 후 모델의 구축했다.
  
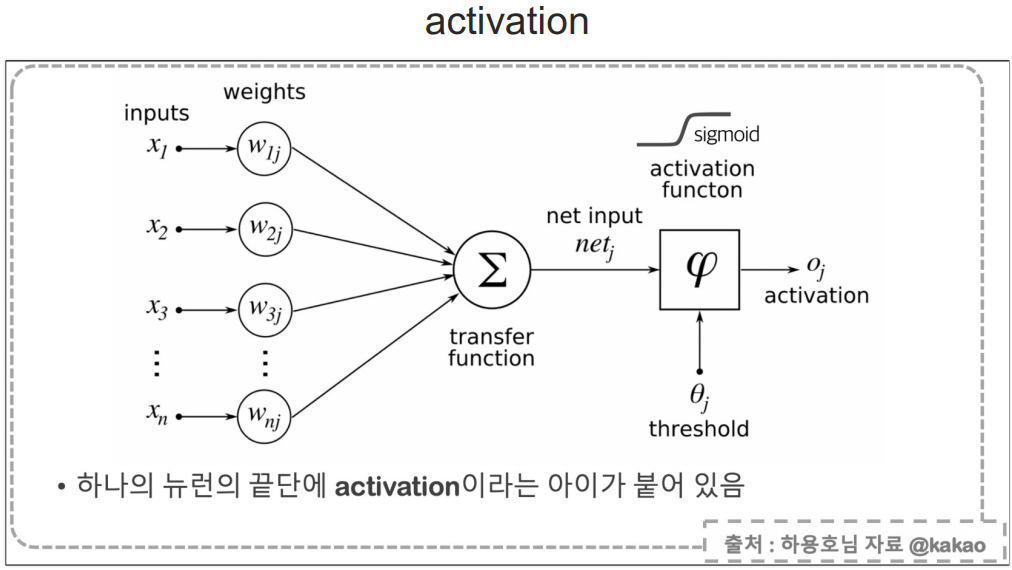
• activation은 layer사이에 계산 방정식?이라고 설명하는 것이 정확할지 모르겠지만 다음 layer로 넣어갈 떄 사용하는 방정식이다.
  
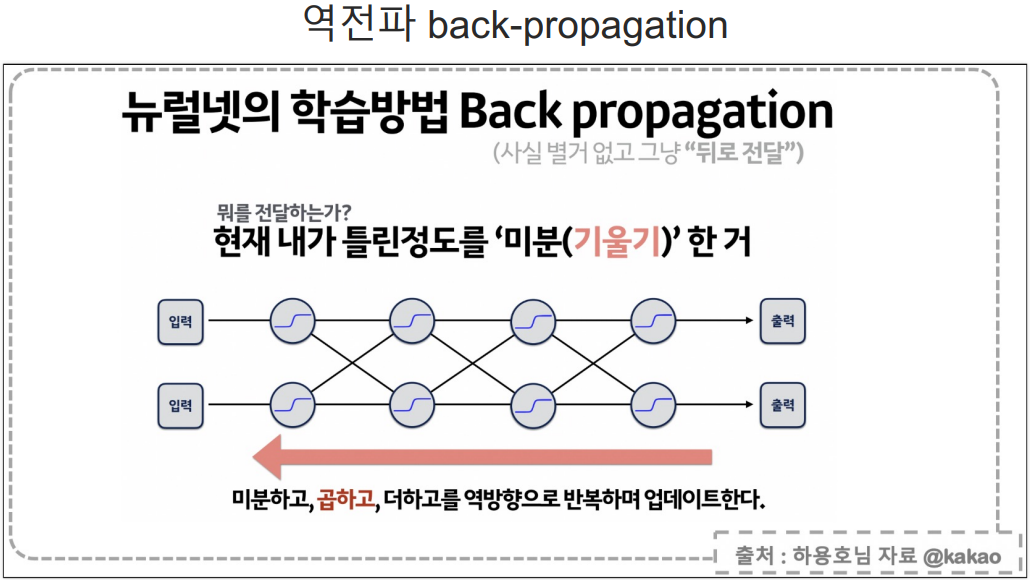
• 위에 말한 것과 같이 여러 layer를 쓸 때는 뒤로 loss와 미분을 통해 계산해서 값을 구한다.
  
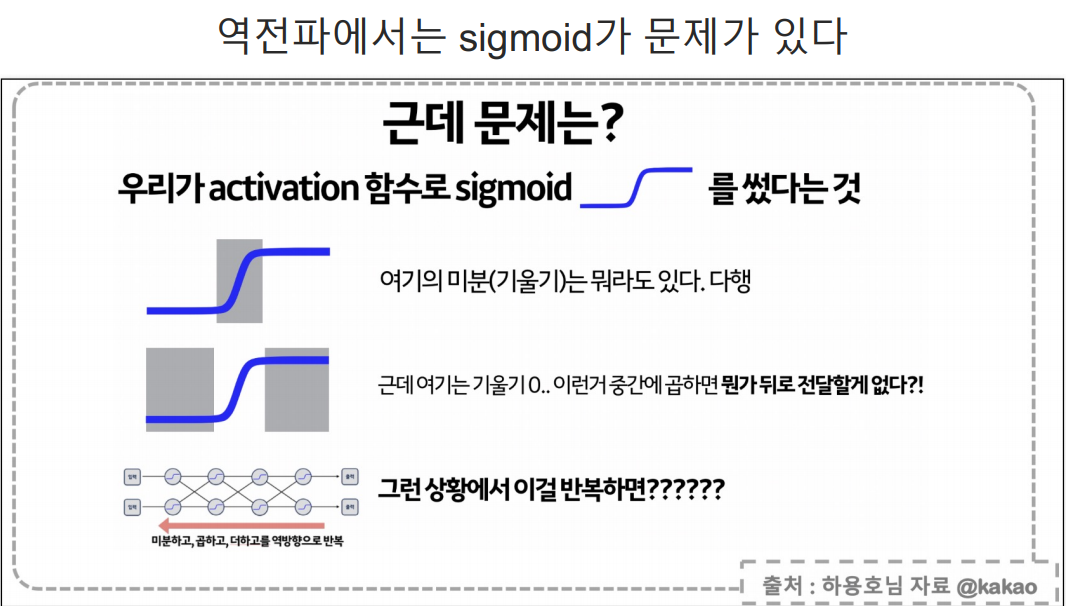
• 하지만, sigmoid는 기울기가 있기는 하지만, 우리가 gradient Descent방법을 사용할 때처럼 u자 형태의 2차함수가 아니기에 정확한 미분값을 구할 수 없다.
  
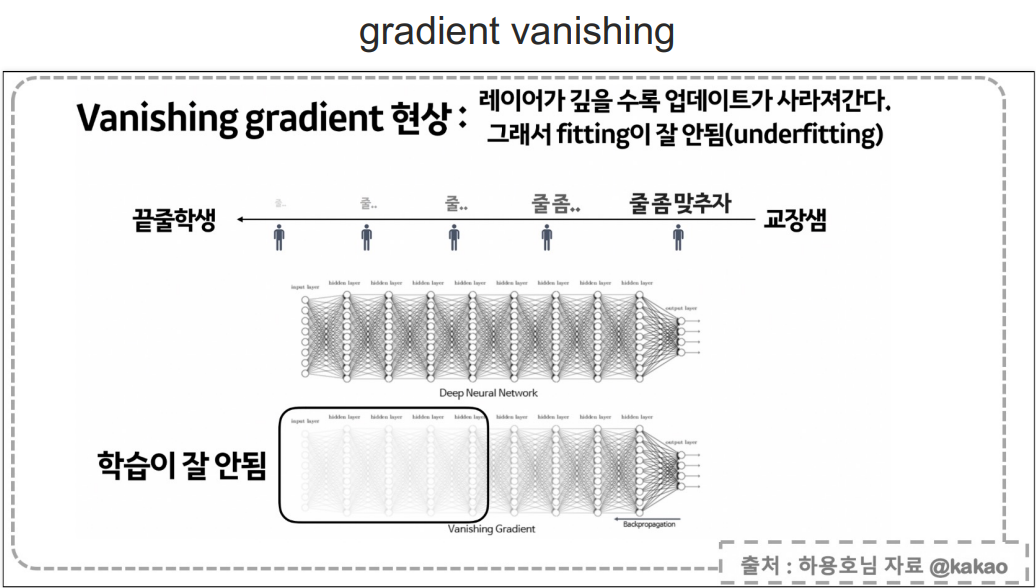
• 그래서 layer가 많아질수록 값이 너무 작아져서 제대로 fit이 안되는데, 이걸 Vanishing Gradent현상이라고 한다.
  
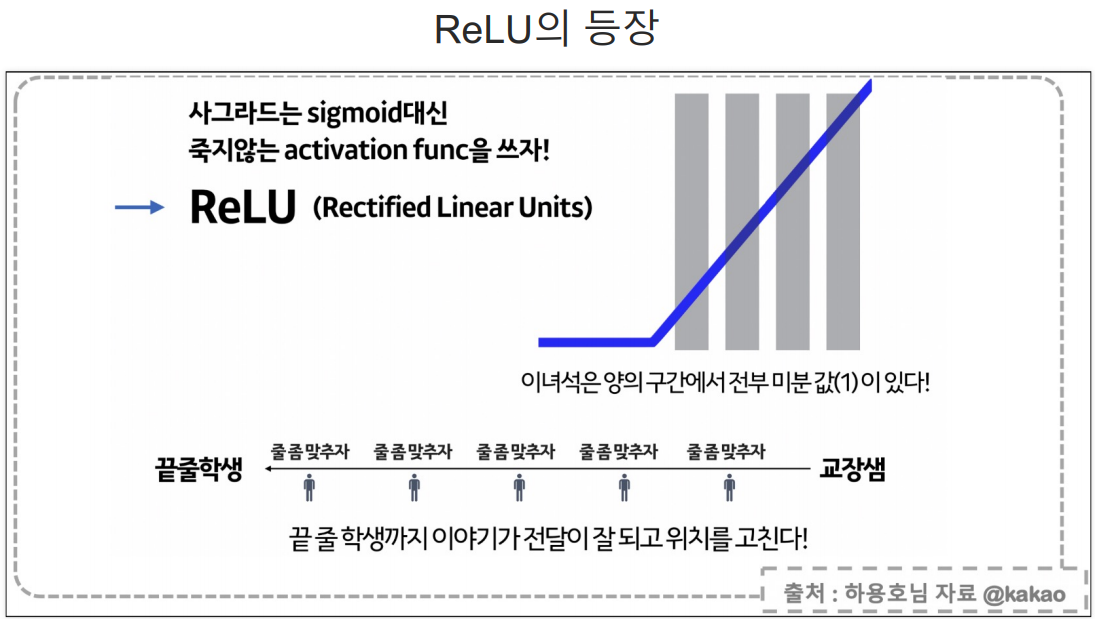
• 해당 문제를 해결하기 위해 만들어진 activation이 relu이다.
  
• 그리고 마지막으로 출력값을 낼 때 쓰는 대표적인 activation으로 원래 output값, sigmoid(이진 범주), softMax(Categorical) 3개로 쓴다.
  
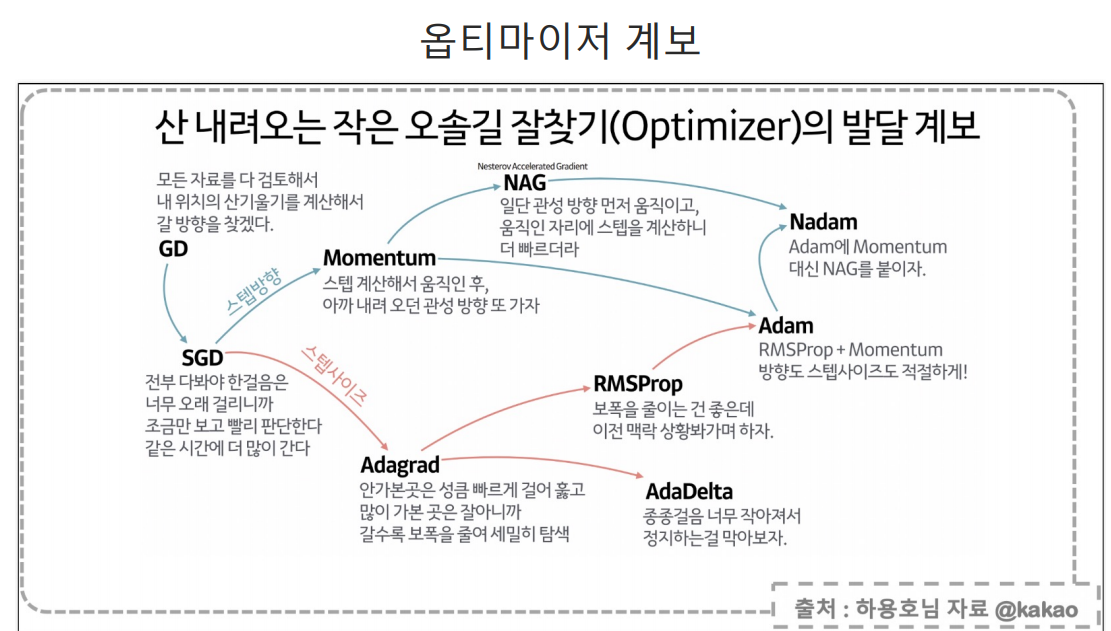
• 그리고 compile할 때 쓰는 optimizer은 최적화 방식으로 Gradient Descent를 기반으로 많은 발전이 이루어졌는데, 특정한 경우가 아니면 Adam()를 사용한다.(만드신 개발자 진짜 감사합니다...)
  
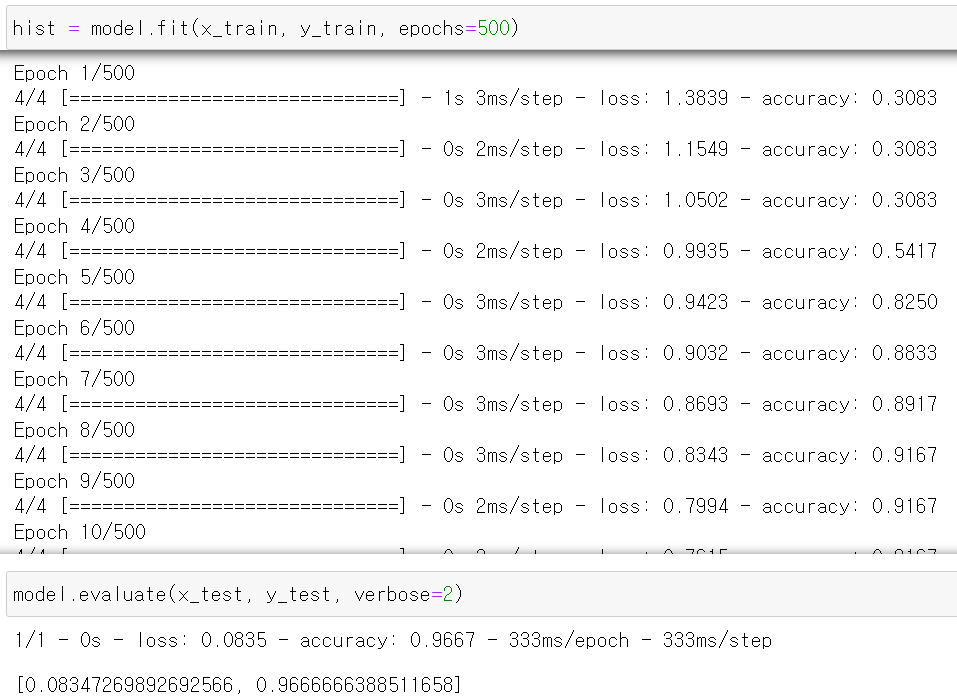
• 이제 모델에 데이터를 교육시키고, 결과를 확인해보니 96%의 정확도를 보인다.
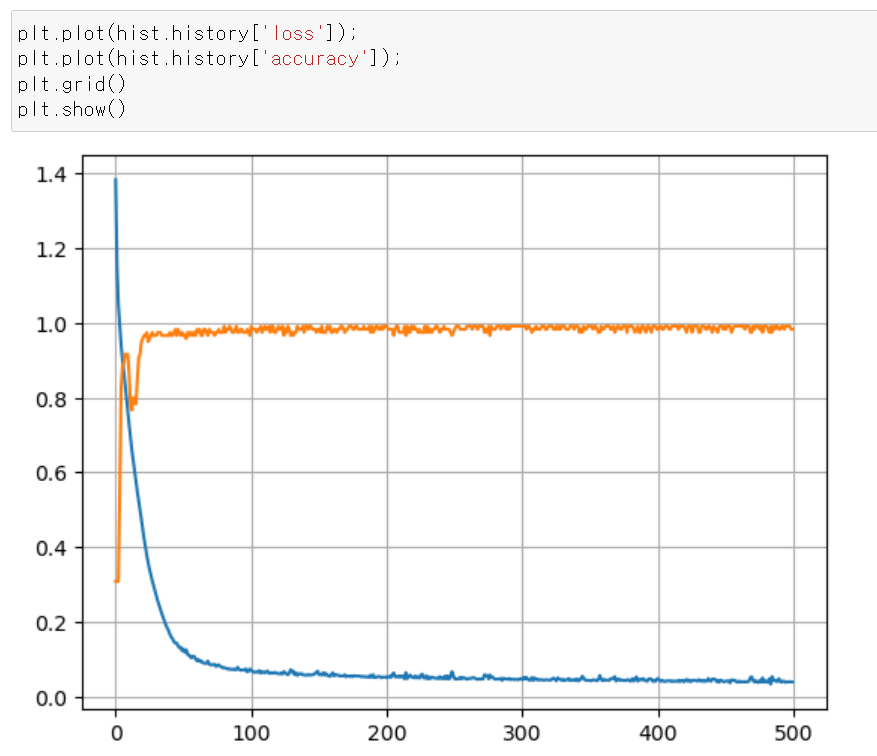
• 점점 loss값은 떨어지고, accuracy는 올라가다가 어느 구간에서 일정한 수치를 보인다.