DeepLearning_from_scratch

안선경·2023년 4월 29일

DL_study

목록 보기

16/23

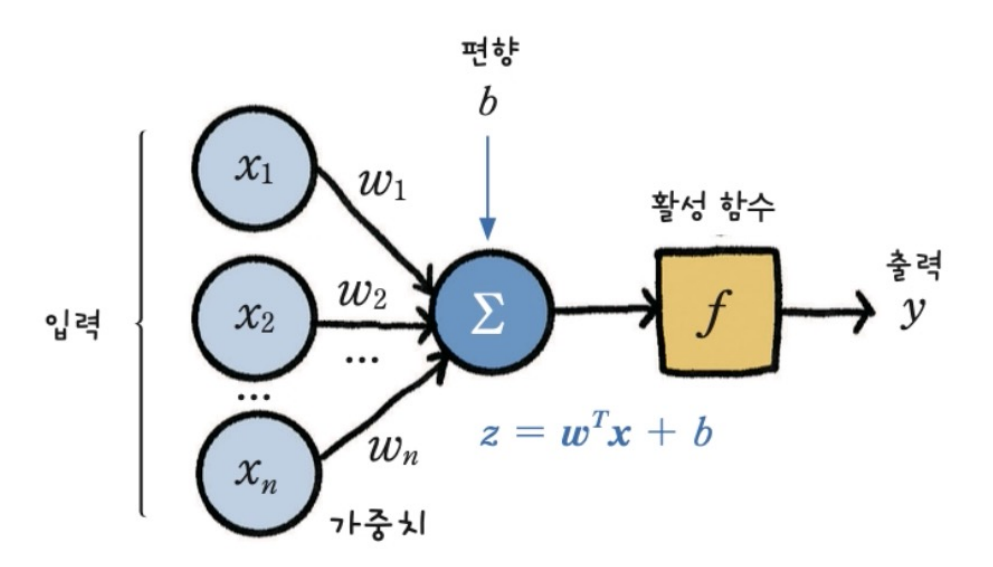
이번에는 DeepLearnnig의 연산원리를 알아보자
기본적으로 각 데이터 x1, x2...xn에 w1, w2, w3...wn을 곱해서 하나의 결과를 출력하게 된다.
DeepLearning에서는 이를 forward pass이라고 하는데 쉽게 말해 그냥 순서대로 계산을 하는 것이다.
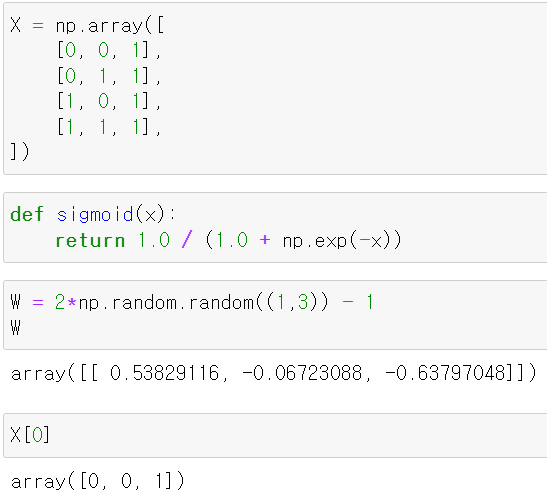
위 그림과 같이 계산을 해봤다.
X에 데이터를 저장하고, Sigmoid값으로 변환하는 함수를 만들었다.
그리고 가중치 w는 임의의 숫자로 만들었다.
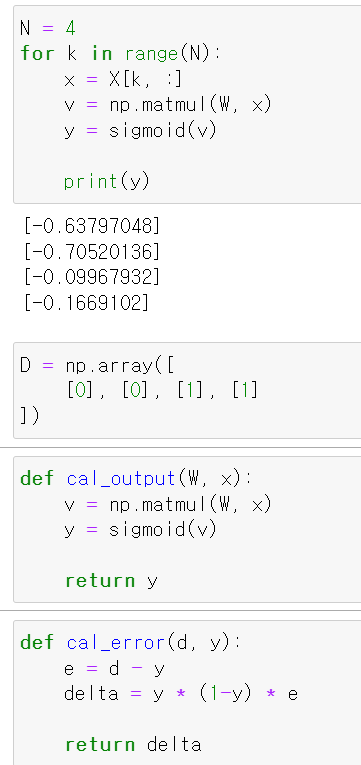
이제 각 데이터에 가중치를 곱하고 sigmoid로 변환했을 때 값이 출력된다.
그리고 Label값으로 0, 0, 1, 1를 저장했다.
이제 순방향으로 계산하는 출력값 함수와 출력값을 바탕으로 delta값을 구해 가중치를 조정할 함수를 만들었다
sigmoid의 미분을 계산해보면 결국 $sigmoid(x) \times (1-sigmoid(x)$ 의 값을 출력한다.
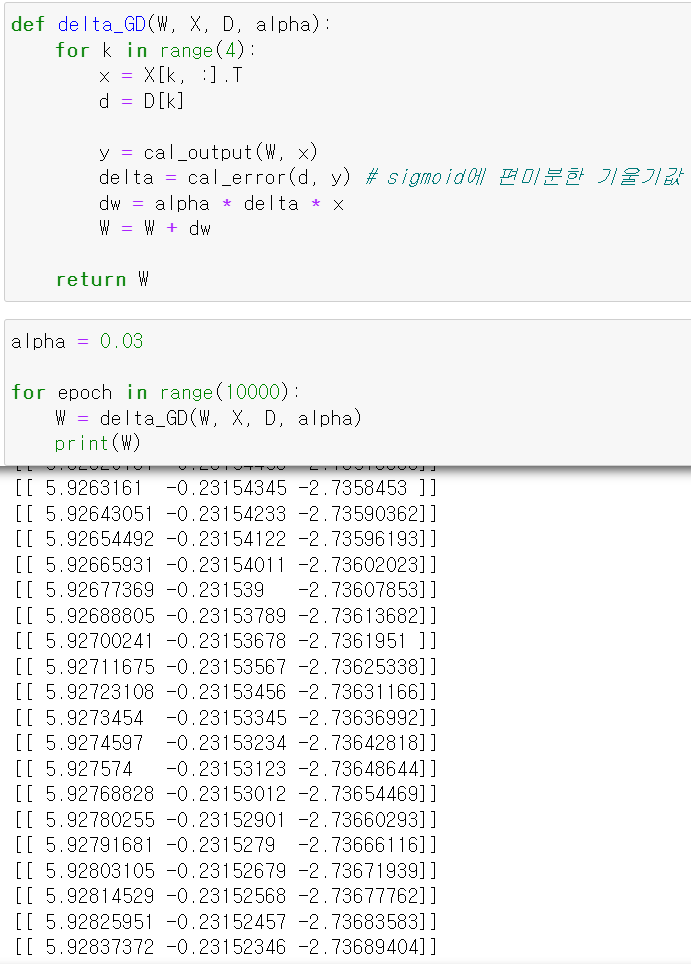
이제 출력값을 만들고 그 출력값에 대한 Backpropagation을 통해 가중치를 조정하는 함수를 만들고
해당 함수를 epoch 10000을 주고 w값을 교육시켰다.
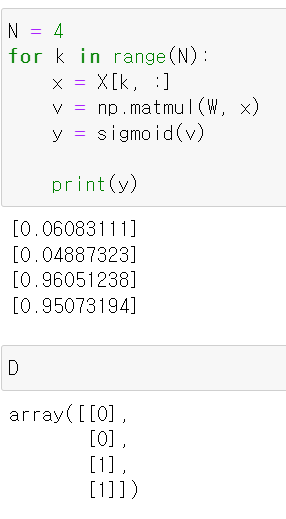
이제 조정한 w값을 바탕으로 순방향으로 계산한 결과 실제값과 예측값이 맞았다.
하지만 위 데이터를 바탕으로 같은 방법을 사용해 교육시켰지만, 제대로된 정답이 나오지 않았다.
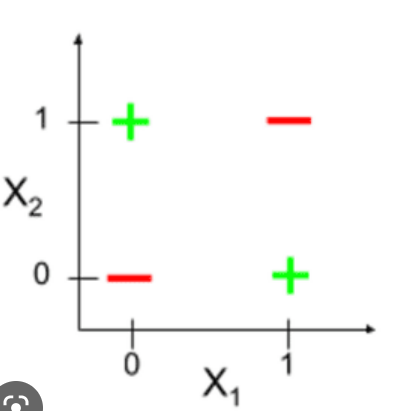
그 이유는 위 그림과 같이 하나의 직선 곧 하나의 계층(Layer)로 구분을 할 수 없기 때문이다.
해당 그림에서 +, -를 구분하기 위해서는 하나의 직선으로 불가능하다.
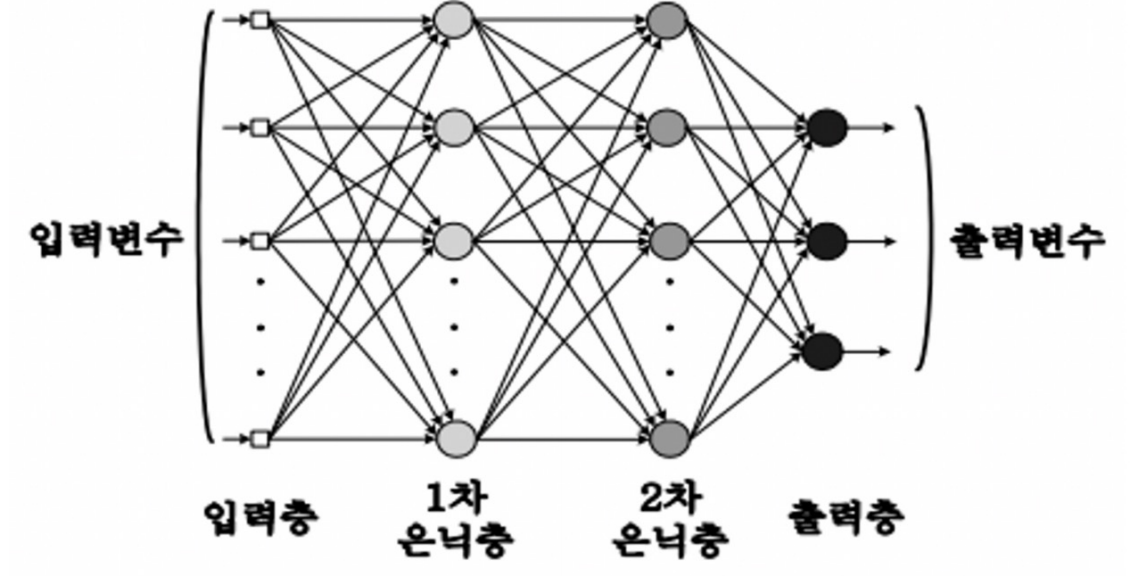
그래서 이렇게 여러 Layer를 만들고 이를 은닉 계층으로 말하며, 여러 직선을 구현할 수 있게 만들었다.
이제 해당 그림과 같이 모델을 구축하기 위해 두 개의 delta를 만드는 함수와 해당 함수를 바탕으로 Backpropagation을 구현하는 함수를 만들었다.
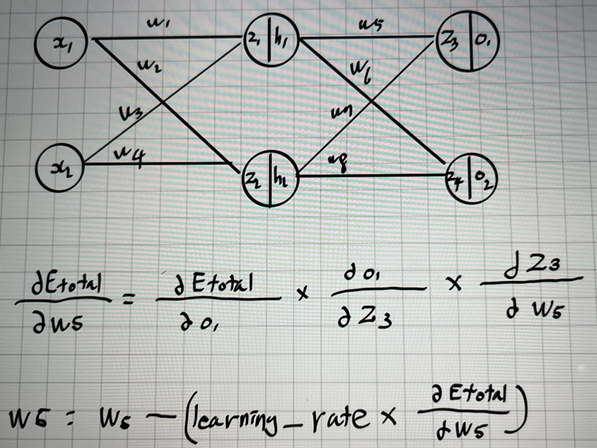
직접 그린 그림인데, delta부분이 이해를 돕기 위해 그렸다.(글씨체가 쪼금...보기 어려운 점 죄송합니다...!)
w5의 가중치를 구하기 위해서는 앞의 모든 단계의 미분값을 더해서 곱하는데 이를 Chain rule이라고 한다.
즉, 최종 loss값에 대한 x1을 미분하기 위해 뒤에서 앞으로 반대 방향으로 미분값을 순차적으로 업데이트하며 최종적으로 $\frac{\delta loss}{\delta x}$ 값을 구하기 위해 Backpropagation과정을 가진다.
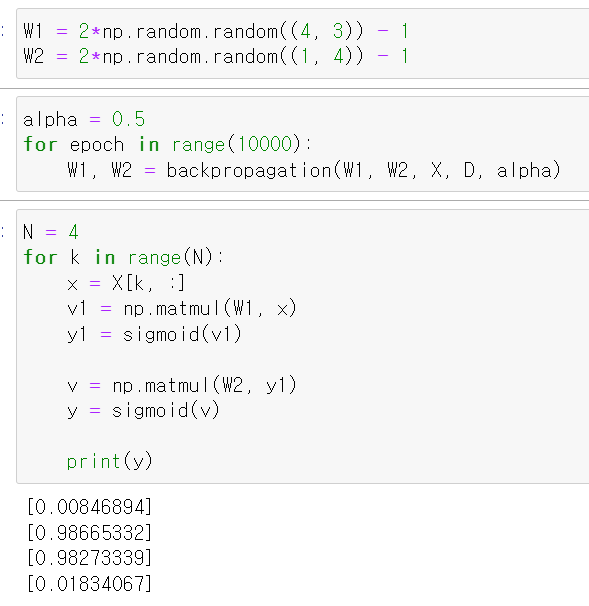
이제 임의의 가중치값을 변수에 저장하고, learning_rate값을 0.5로 주고 돌려본 결과 정사적으로 0 1 1 0값이 출력됐다.
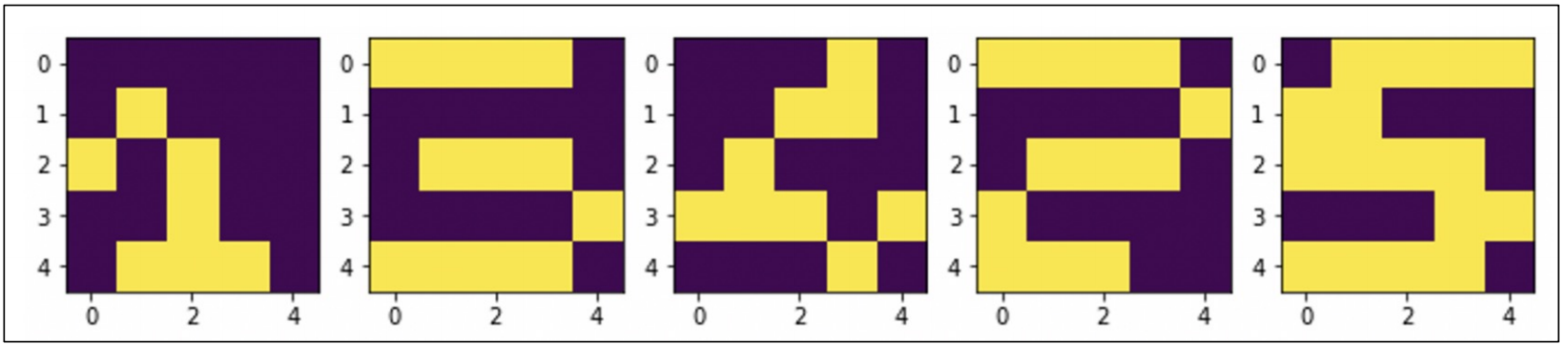
이제 위 그림과 같은 결과값을 예측하는 모델을 구축해봤다.
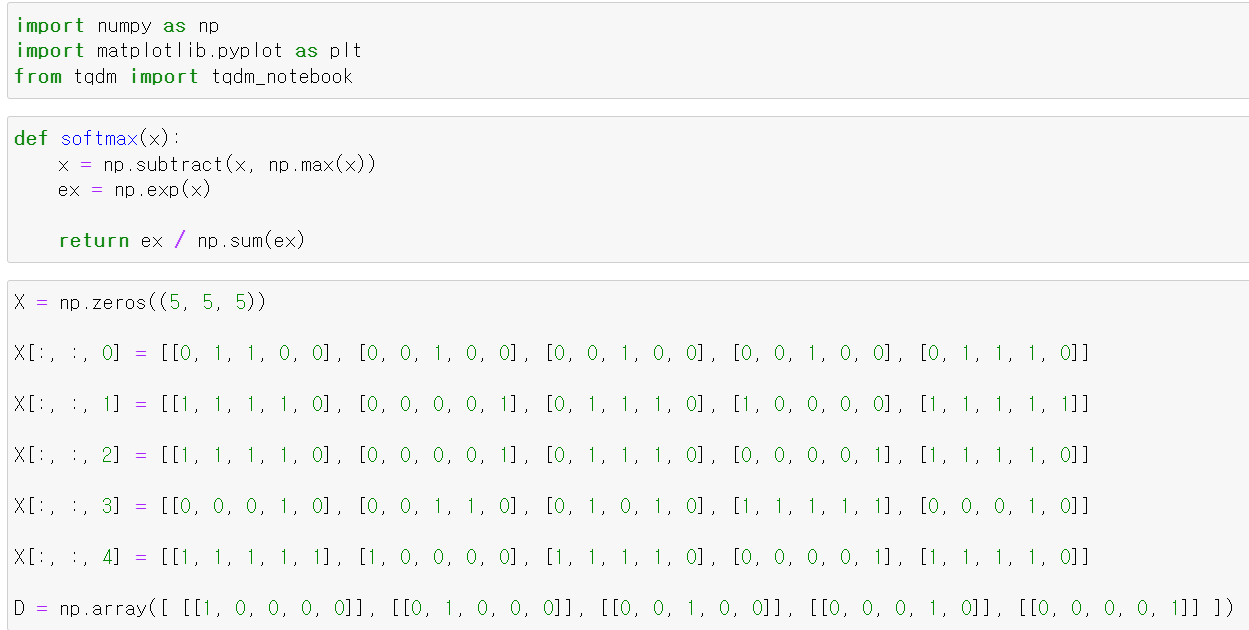
먼저 softmax에 대한 활성화함수 기능을 하는 함수를 만들고
그림과 같이 이미지를 만들기 위해 수작업으로 데이터를 만들었다.
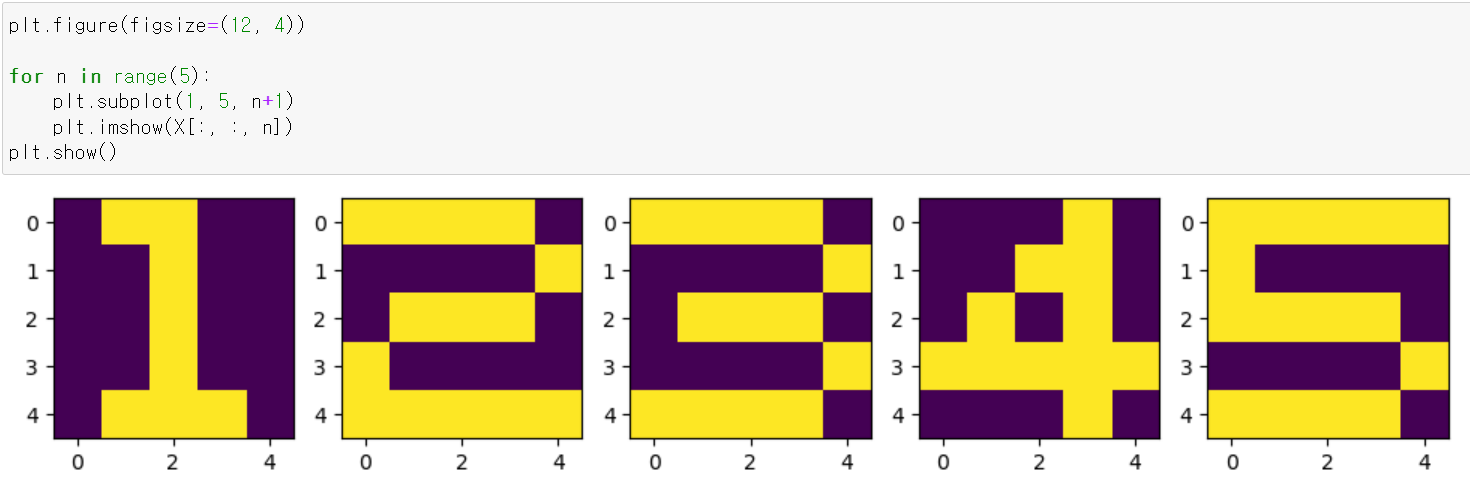
plt.imshow를 통해 그려보니 정상적으로 나왔다.
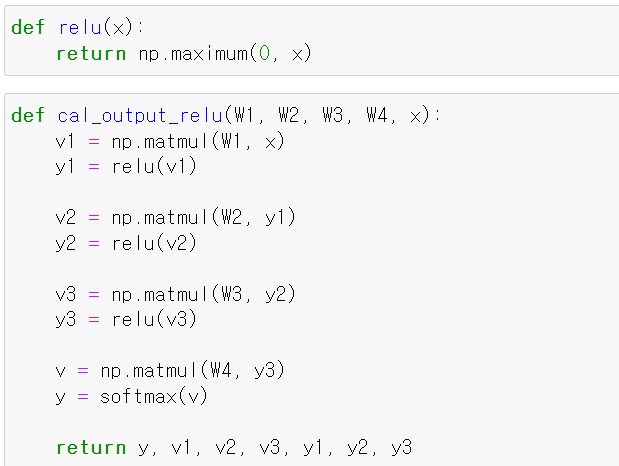
이제 relu 활성화 함수 기능을 하는 함수를 만들고, 순방향으로 계산하는 함수를 만들었다.
relu의 경우 0보다 작을 경우 0의 값을 준다.
이제 backpropagation을 구현하는 함수를 만들었다.
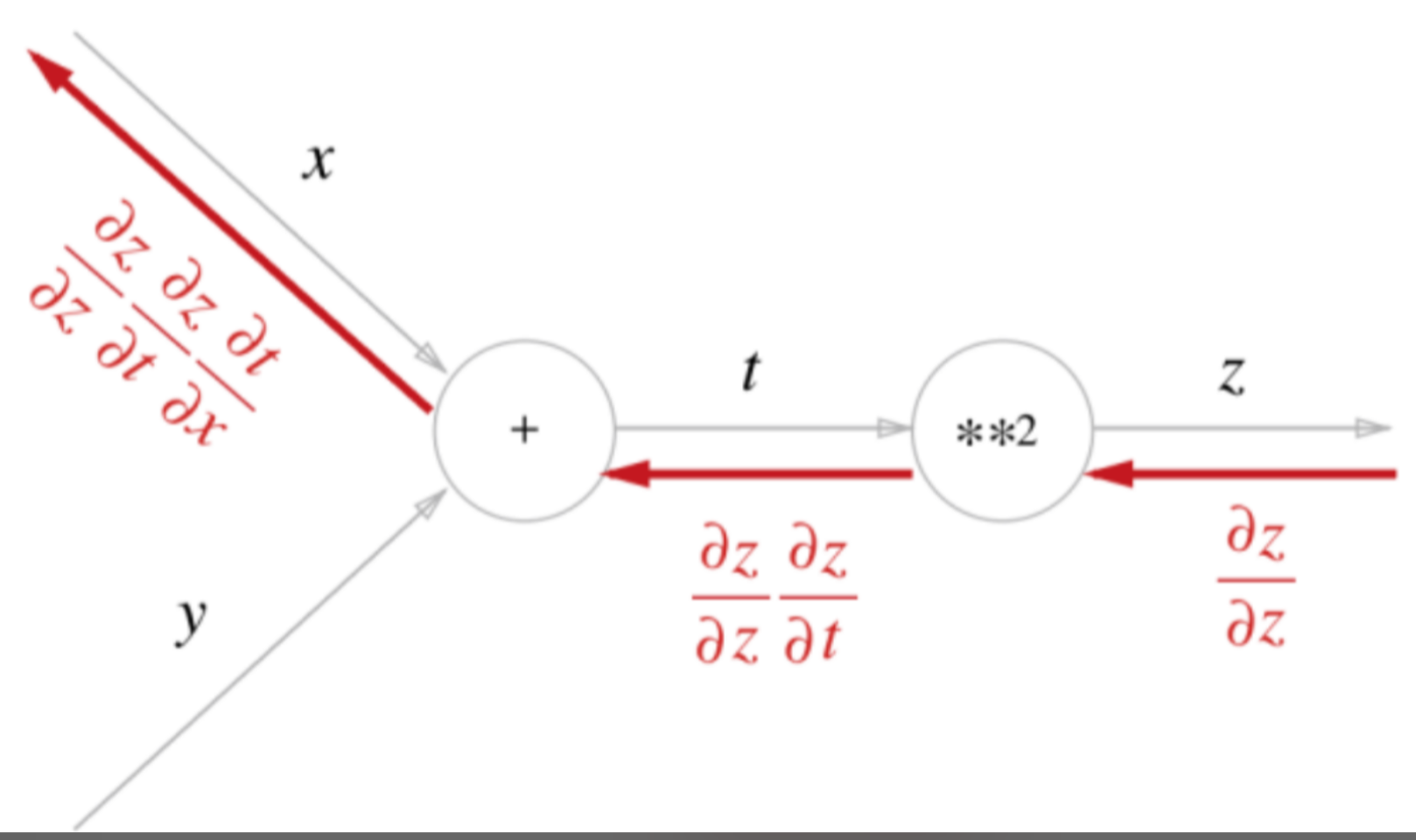
chain Rule의 이해를 돕기 위해 사진을 넣었다.
이제 가중치를 업데이트하는 함수를 만들고, 각 구한 데이터를 바탕으로 반복적으로 가중치를 업데이트해서 최종적인 가중치를 만드는 함수를 만들었다.
이제 4개의 임의의 가중치를 만들고 learning_rate를 0.01로 저장한 뒤
10000의 epoch를 돌려 가중치를 조정했다.
그리고 구한 가중치를 순방향으로 계산해서 결과값을 리턴하는 함수를 만들고
결과를 확인하기 위해 각 값에 넣어보니
실제값과 예측값이 일치한다.