빅 오
빅 오(Big O)는 입력값이 무한대로 향할 때 함수의 상한을 설명하는 수학적 표기 방법이다. 입력의 크기가 충분히 클 경우에 알고리즘의 효율성에 따라 수행 시간이 크게 차이가 날 수 있기 때문에 코드를 작성할 때에 빅 오를 고려하며 작성한다면 더 좋은 코드를 만들어 낼 수 있다.
시간 복잡도란 어떤 알고리즘을 수행하는 데 걸리는 시간을 설명하는 계산 복잡도를 의미하며, 빅 오로 표기된다. 빅 오로 시간 복잡도를 계산할 때에는 최고차항만을 표기하고 계수는 무시한다. 만약 시간 복잡도가 입력값 n에 대해 4n^2+3n+2일 경우 빅 오는 O(n^2)가 된다.
빅 오 표기법의 종류
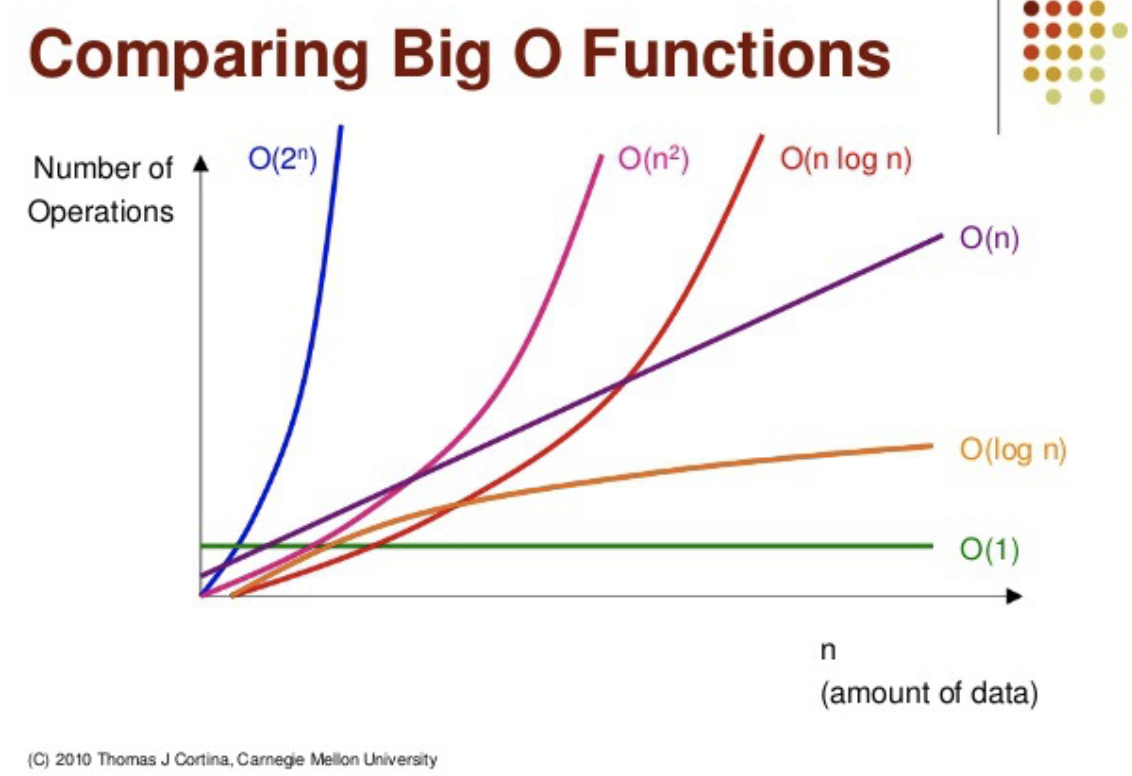
O(1)
입력값이 아무리 커도 실행 시간은 일정하다. 최고의 알고리즘이라 할 수 있다. 상수 시간을 갖는 알고리즘은 찾을 수만 있다면 정말 가치있지만 그러한 알고리즘을 찾기란 매우 어렵다. 또한 상수 시간에 실행된다 해도 상수값이 상상을 넘어설 정도로 매우 크다면 사실상 일정한 시간의 의미가 없다. 최고의 알고리즘이 될 수 있지만 그만큼 신중해야 한다.
- 해시 테이블의 조회 & 삽입
O(log n)
지금부터 설명되는 빅 오는 모두 입력값에 영향을 받는다. 그러나 로그는 매우 큰 입력값에도 크게 영향을 받지 않는 편으로 왠만한 n의 크기에 대해서도 매우 견고하다.
- 이진 검색
O(n)
입력값만큼 실행 시간에 영향을 받으며 알고리즘을 수행하는 데 걸리는 시간은 입력값에 비례한다. O(n) 알고리즘을 선형 시간 알고리즘이라고도 부른다. 정렬되지 않은 리스트에서 최댓값 또는 최솟값을 찾는 경우가 이에 해당하며 이 값을 찾기 위해 모든 입력값을 적어도 한 번 이상은 살펴봐야 한다.
- 최댓값/최솟값 찾기
O(n log n)
병합 정렬을 비롯한 대부분의 효율 좋은 정렬 알고리즘이 해당한다. 적어도 모든 수에 대해 한 번 이상은 비교해야 하는 비교 기반 정렬 알고리즘은 아무리 좋은 알고리즘도 O(n log n)보다 빠를 수 없다. 물론 입력값이 최선인 경우, 비교를 건너뛰어 O(n)이 될 수 있으며 팀소트가 이런 로직을 갖는다.
- 병합 정렬
O(n^2)
버블 정렬같은 비효율적인 정렬 알고리즘이 이에 해당한다.
- 버블 정렬
O(2^n)
피보나치수를 재귀 계산하는 알고리즘이 이에 해당한다. n^2와 2^n이 헷갈릴 수 있는데 이 둘은 매우 다르다. 처음에는 비슷해보일 수 있지만 입력값이 커질 수록 2^n이 훨씬 더 커지는 것을 볼 수 있다.
- 피보나치 수열 재귀 계산
O(n!)
각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 외판원 문제를 브루트 포스로 풀이 할 때가 해당되며 가장 느린 알고리즘으로, 입력값이 조금만 커져도 웬만한 다항 시간 내에는 계산이 어렵다.
- 브루트 포스 알고리즘
분할 상환 분석
시간 또는 메모리를 분석하는 알고리즘의 복잡도를 계산할 때 알고리즘 전체를 보지 않고 최악의 경우만을 살펴보는 것은 지나치게 비관적이라는 이유로 분할 상환 분석 방법이 등장하였다.
분할 상환 분석은 빅 오와 함께 함수의 동작을 설명할 때 중요한 분석 방법 중 하나이다, 분할 상환 분석이 유용한 예로 '동적 배열'을 들 수 있는데 동적 배열에서 더블링이 일어나는 일은 가끔가다 한번이지만 이로 인해 '아이템 삽입 시 시간 복잡도는 O(n)이다.'라고 얘기하는 것은 지나치게 비관적이고 정확하지도 않다. 따라서 이 경우 반할 상환 또는 상각이라고 표현하는 최악의 경우를 여러 번에 걸쳐 골고루 나눠주는 형태로 알고리즘의 시간 복잡도를 계산할 수 있다. 이렇게 할 경우 동적 배열은 O(n)이 아닌 O(1)이 된다.
병렬화
일부 알고리즘은 병렬화를 통해 실행 속도를 높일 수 있다. 최근 딥러닝의 인기와 함께 병렬화가 큰 주목을 받고 있고 GPU는 병렬 연산을 위한 대표적인 장치이다. CPU보다는 느리지만 수천여개의 코어로 구성되어 있기 때문에 수십개의 코어를 가진 CPU보다 수백 배 더 많은 연산을 동시에 처리할 수 있다. 이처럼 딥러닝 알고리즘을 비롯하여 병렬 연산이 가능한 알고리즘들이 최근에 큰 주목을 받고 있다. 알고리즘 자체의 시간 복잡도 외에도 알고리즘이 병렬화가 가능한지의 여부가 근래 알고리즘의 우수성을 평가하는 매우 중요한 척도 중 하나로 자리 잡았기 때문이다.
