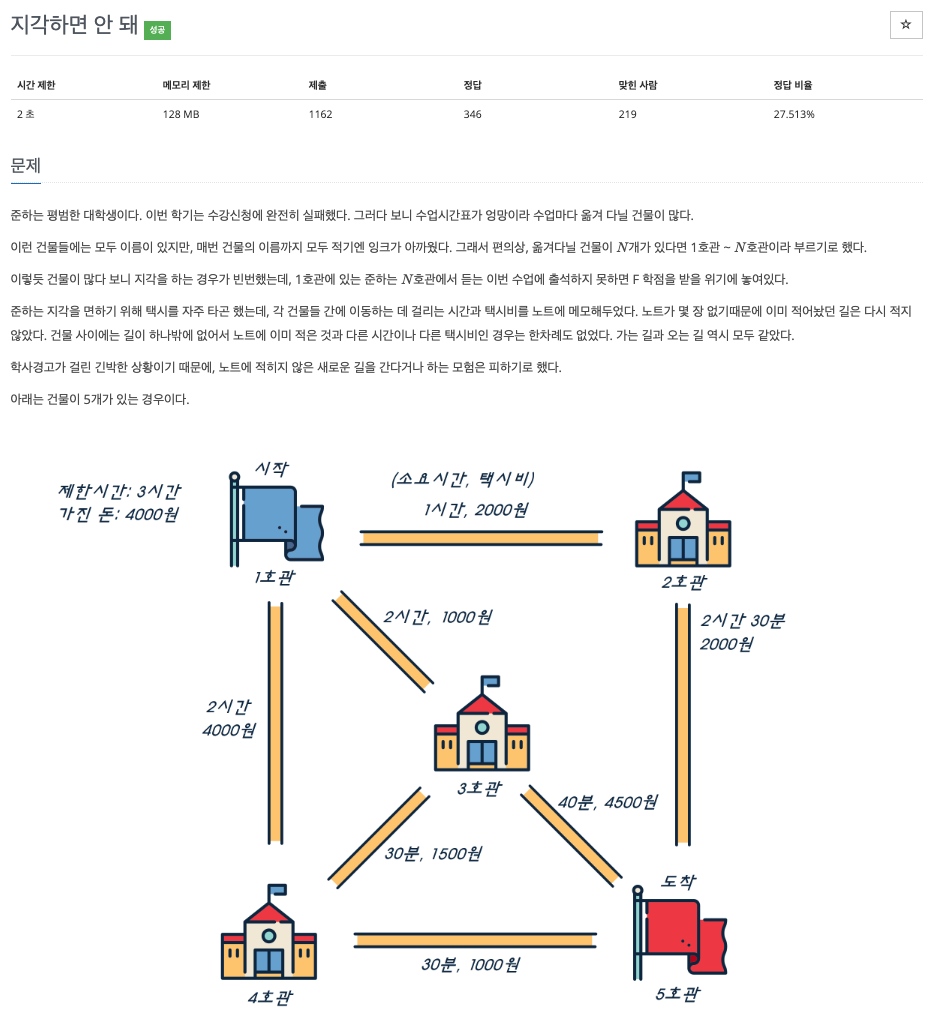
이번 문제는 다익스트라 알고리즘을 통해 해결하였다. 처음에는 비용만 체크하며 탐색을 진행하였는데, 50%에서 오답처리되었다. 그래서 시간도 같이 체크하며 탐색을 진행하였다. 비용을 저장하는 리스트를 2차원 리스트로 선언하여 각 건물과 시간에 대한 비용을 모두 저장하게 하였고, 결과를 구할 때에는 n번 건물에 대한 비용 리스트 중 가장 작은 값을 취하도록 하였다.

Code

import heapq
n = int(input())
t, m = map(int, input().split())
l = int(input())
path = [[] for _ in range(n+1)]
for _ in range(l):
    a, b, time, cost = map(int, input().split())
    path[a].append((b, time, cost))
    path[b].append((a, time, cost))
def find_path():
    q = []
    heapq.heappush(q, (0, 0, 1))
    costs = [[1e9 for _ in range(t+1)] for _ in range(n+1)]
    costs[1][0] = 0
    while q:
        cost, time, cur = heapq.heappop(q)
        if cost > costs[cur][time]:
            continue
        for nxt, tm, cst in path[cur]:
            nxt_cst = cost+cst
            nxt_tm = time+tm
            if nxt_tm <= t and nxt_cst <= m and costs[nxt][nxt_tm] > nxt_cst:
                costs[nxt][nxt_tm] = nxt_cst
                heapq.heappush(q, (nxt_cst, nxt_tm, nxt))
    return min(costs[n])
answer = find_path()
if answer == 1e9:
    answer = -1
print(answer)