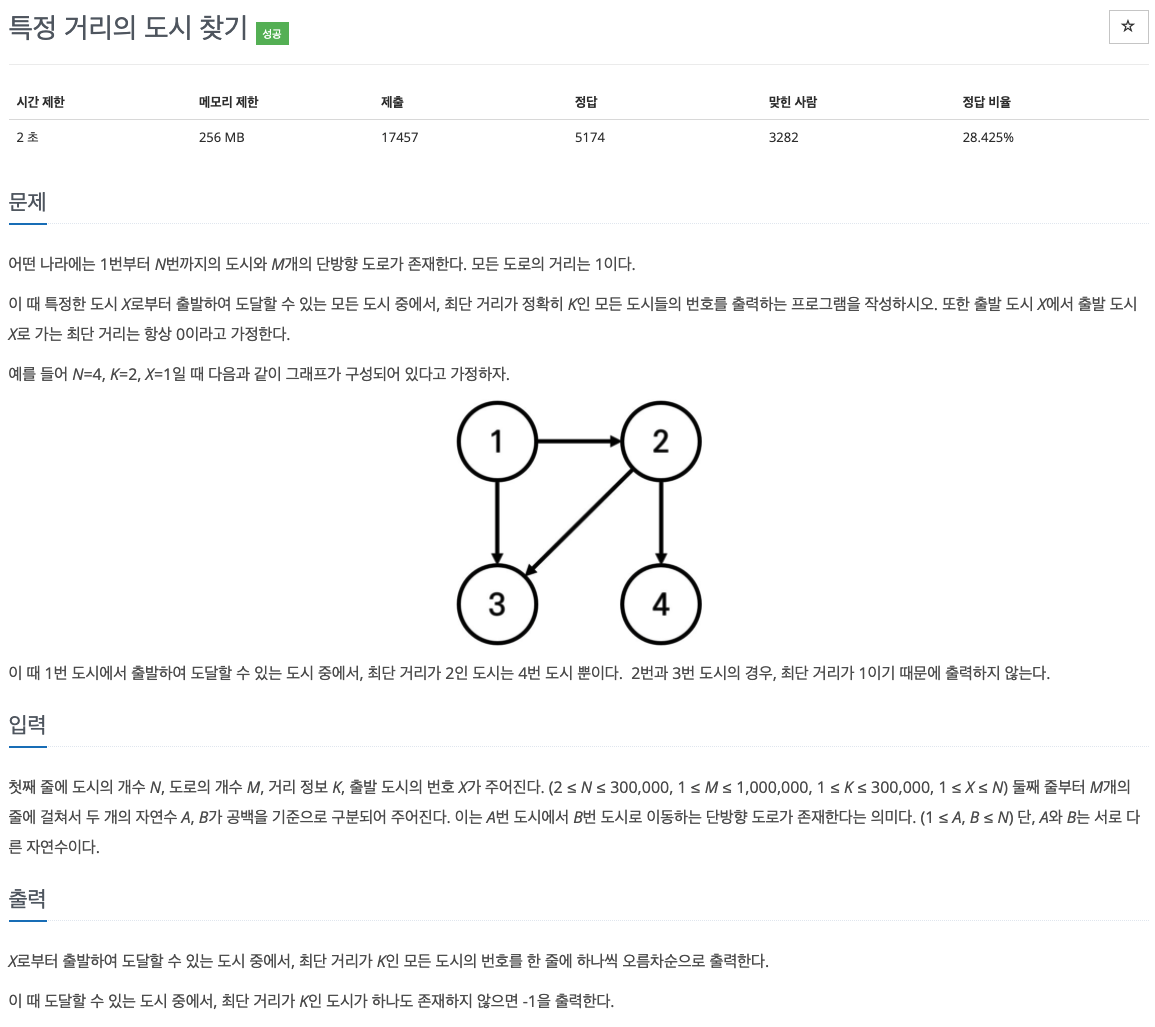
이번 문제는 다익스트라 알고리즘을 통해 해결하였다. 다익스트라 알고리즘으로 접근하여 제출하였지만 시간 초과가 발생하여 input을 sys.stdin.readline으로 변경하고, sys.maxsize를 dist 리스트에 매번 넣는것이 아닌, INF 변수에 sys.maxsize값을 저장하여 dist 리스트에 INF를 넣어 보았다. 이러한 방식으로 코드를 수정하여 제출하니 통과할 수 있었다.

출발 도시에서부터의 각 도시의 거리를 저장하는 리스트 dist를 최대값으로 채운 뒤에 출발 도시에 해당하는 dist는 0으로 갱신해주고, 다익스트라 알고리즘을 통해 각 도시까지의 최단 거리를 구하였다. 최단 거리를 구하는 도중에 현재의 거리가 k와 같다면 정답 리스트에 바로 추가해주었다.

• input을 sys.stdin.readline로 저장한다.
• n, m, k, x를 입력받는다.
• graph를 2차원 리스트로 선언한다.
• m번 반복하는 for문을 돌린다.
  -> a, b를 입력받는다.
  -> graph[a]에 (b, 1)을 넣는다.
• 결과를 저장할 리스트 results를 선언한다.
• 최대값을 저장할 변수 INF에 sys.maxsize를 저장한다.
• 거리를 저장하는 리스트 dist를 INF n+1개로 채운다.
• dist[x]를 0으로 갱신한다.
• 다익스트라에 사용할 큐 q를 최소힙으로 선언하고, (0, x)를 넣어준다. (0은 현재까지의 거리, x는 현재의 위치)
• q가 존재하는 동안 반복하는 while문을 돌린다.
  -> distance, cur을 q에서 추출한다.
  -> 만약 distance가 dist[cur]보다 클 경우, 다음 반복으로 넘어간다.
  -> 만약 distance가 k와 같을 경우, results에 cur을 넣어준다.
  -> graph[cur]을 순회하는 nxt, dst에 대한 for문을 돌린다.
  --> cost에 distance+dst를 저장한다.
  --> 만약 cost보다 dist[nxt]가 더 클 경우,
  ---> dist[nxt]를 cost로 갱신한다.
  ---> q에 (cost, nxt)를 넣어준다.
• 만약 results가 비어있다면 -1을 출력한다.
• 그 외에는 results를 한줄에 하나씩 출력한다.

Code

import heapq
import sys
input=sys.stdin.readline
n, m, k, x=map(int, input().split())
graph=[[] for _ in range(n+1)]
for _ in range(m):
    a, b=map(int, input().split())
    graph[a].append((b, 1))
results=[]
INF=sys.maxsize
dist=[INF for _ in range(n+1)]
dist[x]=0
q=[]
heapq.heappush(q, (0, x))
while q:
    distance, cur=heapq.heappop(q)
    if distance>dist[cur]:
        continue
    if distance==k:
        results.append(cur)
    for nxt, dst in graph[cur]:
        cost=distance+dst
        if cost<dist[nxt]:
            dist[nxt]=cost
            heapq.heappush(q, (cost, nxt))
if not results:
    print(-1)
else:
    for i in results:
        print(i)