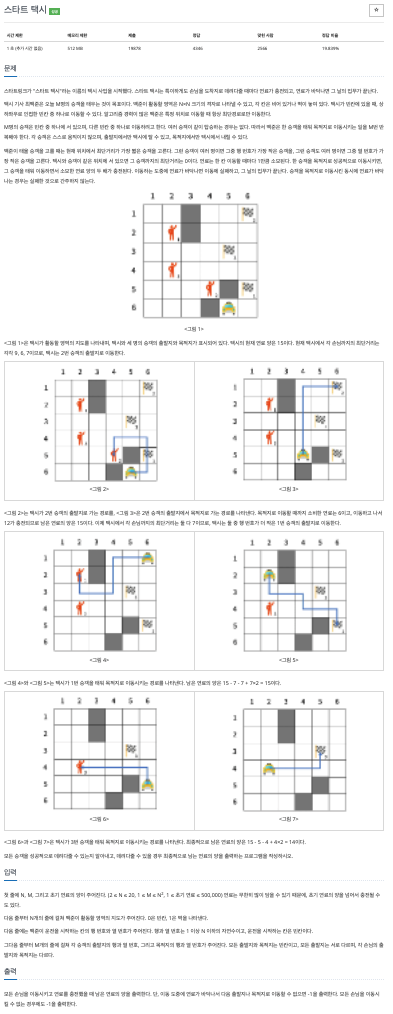
이번 문제는 삼성 기출 문제로, 시간초과와 예외에 걸려 오랜 시간을 투자하였다. 우선 처음에는 bfs함수를 사람의 수만큼 탐색하여 가장 가까운 사람을 찾도록 하였다. 그러나 이럴 경우에 승객이 많아질 경우, bfs함수의 호출 횟수가 늘어 시간초과가 발생한다.

그래서 다익스트라 알고리즘을 통해 각 위치까지의 최단 거리를 저장한 리스트를 생성하도록 하였고, 이를 통해 현재 위치에서 모든 위치까지의 최단 거리를 한번에 구하여 거리를 사용하도록 하여 시간을 단축하였다.

예외는 승객의 도착지에 도착함과 동시에 연료를 모두 소모했을 경우이다. oil<=0일 경우에 -1을 출력하도록 하였는데, 도착했을 경우에 연료가 딱 0이 남았다면 이는 종료 사유가 아니게 되므로 oil<0으로 해줘야 했다. 이를 통해 문제를 해결하였다.

Code

import sys
import heapq
n, m, oil=map(int, input().split())
grid=[list(map(int, input().split())) for _ in range(n)]
a, b=map(int, input().split())
cur=[a-1, b-1]
ps=[]
for i in range(m):
    a, b, c, d=map(int, input().split())
    ps.append((a-1, b-1, c-1, d-1))
ps.sort(key=lambda x:(x[0], x[1]))
dy, dx=[1, 0, -1, 0], [0, 1, 0, -1]
INF=sys.maxsize
def bfs(sy, sx):
    q=[]
    heapq.heappush(q, (0, sy, sx))
    visited=[[False for _ in range(n)] for _ in range(n)]
    visited[sy][sx]=True
    dists = [[INF for _ in range(n)] for _ in range(n)]
    dists[sy][sx]=0
    while q:
        dist, y, x=heapq.heappop(q)
        if dist>dists[y][x]:
            continue
        if dist>oil:
            continue
        for i in range(4):
            ny, nx=y+dy[i], x+dx[i]
            if 0<=ny<n and 0<=nx<n and not visited[ny][nx] and grid[ny][nx]==0:
                if dists[ny][nx]>dist+1:
                    dists[ny][nx]=dist+1
                    visited[ny][nx]=True
                    heapq.heappush(q,(dist+1, ny, nx))
    return dists
while ps:
    d=INF
    idx=0
    dists=bfs(cur[0], cur[1])
    for i in range(len(ps)):
        if dists[ps[i][0]][ps[i][1]]==INF:
            print(-1)
            quit()
        if d>dists[ps[i][0]][ps[i][1]]:
            d=dists[ps[i][0]][ps[i][1]]
            idx=i
    oil-=d
    cur=[ps[idx][0], ps[idx][1]]
    if oil<=0:
        print(-1)
        quit()
    d_dists=bfs(cur[0], cur[1])
    if d_dists[ps[idx][2]][ps[idx][3]]==INF:
        print(-1)
        quit()
    oil-=d_dists[ps[idx][2]][ps[idx][3]]
    if oil<0:
        print(-1)
        quit()
    cur=[ps[idx][2], ps[idx][3]]
    oil+=(d_dists[ps[idx][2]][ps[idx][3]]*2)
    ps.pop(idx)
print(oil)