데크 (Deque) & 우선순위 큐

데크 (Deque)

데크는 더블 엔디드 큐의 줄임말로, 글자 그대로 양쪽 끝을 모두 추출할 수 있는 큐를 일반화한 형태의 추상 자료형(ADT)이다.
데크는 양쪽에서 삭제와 삽입을 모두 처리할 수 있으며 스택과 큐의 특징을 모두 가지고 있다. 이 추상 자료형의 구현은 배열이나 연결 리스트 모두 가능하지만 특별히 다음과 같이 이중 연결 리스트로 구현하는 편이 가장 어울린다.

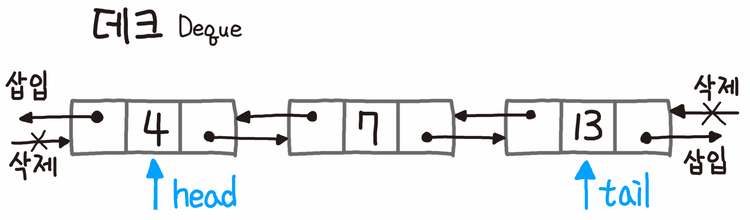
위의 그림과 같이 head와 tail이라는 이름의 두 포인터를 가지고 새로운 아이템이 추가될 때마다 앞 또는 뒤로 연결시켜주기만 하면 된다. 연결 후에는 포인터를 이동시켜야 한다.

LeetCode 641.Design Circular Deque

다음 연산을 제공하는 원형 데크를 디자인하라.

Solution 1 이중 연결 리스트를 이용한 데크 구현

이 문제는 원형 데크를 구현하는 문제이다. 이중 연결 리스트를 통해 구현하였다. 우선 초기화 함수를 다음과 같이 작성하였다.

def __init__(self, k:int):
  self.head, self.tail = ListNode(None), ListNode(None)
  self.k, self.len = k, 0
  self.head.right, self.tail.left = self.tail, self.head

head, tail포인터를 구현하고, 최대 길이 정보를 k로 설정한 뒤에 현재 길이 정보를 담는 변수 len을 0으로 따로 정의하였다.

앞쪽에 노드를 추가하는 연산인 insertFront()는 다음과 같이 구현하였다.

def insertFront(self, value: int) -> bool:
  if self.len == self.k:
      return False
  self.len+=1
  self._add(self.head, ListNode(value))
  return True

노드 삽입 시에 최대 길이를 벗어날 경우에는 False를 반환하도록 하였고 그 외에는 _add() 메소드를 사용해 head위치에 노드를 삽입한다.

뒤쪽에 추가하는 연산 insertLast() 또한 비슷하게 구현하였다. 다른 점은 head 대신에 tail.left에 삽입한다는 점이다.

insertFront(), insertLast()에서 사용할 메소드 _add()는 다음과 같이 구현하였다.

def _add(self, node: ListNode, new: ListNode):
  n = node.right
  node.right = new
  new.left, new.right = node, n
  n.left = new

이중 연결 리스트에서의 삽입은 이미 있는 노드를 찢어내고 그 사이에 새로운 노드 new를 삽입하는 형태가 된다.

삭제 또한 크게 다르지 않다. 앞쪽 삭제의 경우 head의 노드를, 뒷쪽 삭제의 경우 tail의 노드를 처리한다.

class MyCircularDeque:

    def __init__(self, k: int):
        self.head, self.tail = ListNode(None), ListNode(None)
        self.k, self.len = k, 0
        self.head.right, self.tail.left = self.tail, self.head

    def _add(self, node: ListNode, new: ListNode):
        n = node.right
        node.right = new
        new.left, new.right = node, n
        n.left = new
        
    def _del(self, node: ListNode):
        n = node.right.right
        node.right = n
        n.left = node
        
    def insertFront(self, value: int) -> bool:
        if self.len == self.k:
            return False
        self.len += 1
        self._add(self.head, ListNode(value))
        return True

    def insertLast(self, value: int) -> bool:
        if self.len == self.k:
            return False
        self.len += 1
        self._add(self.tail, ListNode(value))
        return True

    def deleteFront(self) -> bool:
        if self.len == 0:
            return False
        self.len -= 1
        self._del(self.head)
        return True

    def deleteLast(self) -> bool:
        if self.len == 0:
            return False
        self.len -= 1
        self._del(self.tail.left.left)
        return True

    def getFront(self) -> int:
        return self.head.right.val if self.len else -1

    def getRear(self) -> int:
        return self.tail.left.val if self.len else -1

    def isEmpty(self) -> bool:
        return self.len == 0

    def isFull(self) -> bool:
        return self.len == self.k

사실 원형 데크를 이중 연결 리스트로 구현하게 되면 원형의 이점을 전혀 살릴 수 없게 된다. 원형 데크의 이점을 살리기 위해서는 연결 리스트가 아닌 배열로 풀어야 한다. 원형으로 구현하는 이유는 뒤쪽으로 요소를 채우다가 공간이 다 차게 되면 tail과 head를 연결하여 앞쪽의 빈 공간을 활용하려는 의도인데 연결 리스트는 애초에 빈 공간을 허용하지 않기 떄문에 의미가 없어진다. 그리고 데크는 맨 처음과 맨 끝의 값을 추출할 뿐 맨끝의 다음 값을 추출하는지 등의 연산이 존재하지 않기 때문에 연결되어있을 필요가 없다.

우선순위 큐

우선순위 큐는 큐 또는 스택과 같은 추상 자료형과 유사하지만 추가로 각 요소의 '우선순위'와 연관되어 있다.
스택은 LIFO, 큐는 FIFO의 특징을 가진다. 이와 다르게 우선순위 큐는 어떠한 특정 조건에 따라 우선순위가 가장 높은 요소가 추출되는 자료형이다. 대표적으로 최대값 추출을 예로 들 수 있는데 [1, 5, 3, 4, 2] 배열을 최대값 추출 우선순위 큐에 넣으면 5, 4, 3, 2, 1 순으로 추출된다.

이는 정렬 알고리즘을 사용하면 우선순위 큐를 만들 수 있다는 의미이다. n개의 요소를 정렬하는데 S(n)의 시간이 필요하다면 새 요소를 삽입하거나 삭제하는데는 O(S(n))의 시간 복잡도가 소요될 것이다. 내림차순으로 정렬했을 때 최대값을 가져오는 데는 맨 앞의 값을 가져오기만 하면 되기 때문에 O(1)에 해결된다. 보통 정렬은 O(n log n)의 시간 복잡도가 필요하므로 O(S(n))은 O(n log n) 정도가 소요되지만 실제로는 이처럼 단순 정렬보다는 힙 정렬 등의 효율적인 방법을 활용한다.

LeetCode 23.Merge k Sorted Lists

k개의 정렬된 리스트를 1개의 정렬된 리스트로 병합하라.

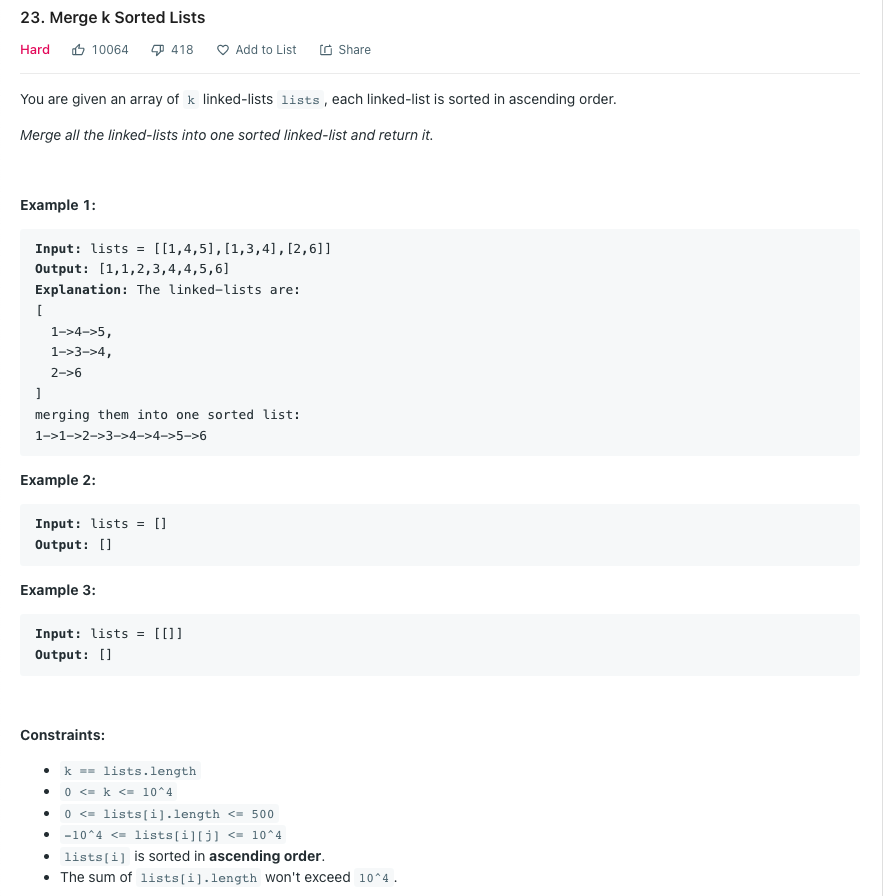
Solution 1 우선순위 큐를 이용한 리스트 병합

리트코드에는 어려움으로 표시되어 있지만 우선순위 큐를 이용하면 쉽게 해결할 수 있는 문제이다. 파이썬에서 우선순위 큐는 heapq 모듈을 사용하여 구현할 수 있다.

for lst in lists:
    heapq.heappush(heap, (lst.val, lst))

이 코드를 통해 각 연결 리스트의 루트를 힙에 저장한다. 파이썬의 heapq 모듈은 최소힙을 지원하기 때문에 lst.val이 작은 순서대로 pop()할 수 있다. 그러나 이 코드를 실행하면 중복된 값을 넣을 수 없다는 에러 메세지가 뜨게 된다. 동일한 값은 heappush() 함수에서 에러를 발생시키기 떄문에 중복된 값을 구분할 수 있는 추가 인자가 필요하다. 에러 방지를 위한 코드는 다음과 같다.

for i in range(len(lists)):
    ...
    heapq.heappush(heap, lists[i].val, i, lists[i]))

이제 heappop()을 통해 값을 추출하면 작은 수부터 나오기 때문에 이 값을 result에 하나씩 추가하면 된다. k개의 연결 리스트가 모두 힙에 계속 들어 있어야 그 중에서 가장 작은 노드가 항상 차례대로 나올 수 있기 떄문에 추출한 연결 리스트의 그 다음 노드는 다음과 같이 다시 힙에 추가해야 한다.

while heap:
    node = heapq.heappop(heap)
    idx = node[1]
    result.next = node[2]
    
    result = result.next
    if result.next:
        heapq.heappush(heap, (result.next.val, idx, result.next))

이렇게 힙이 빌때까지 반복하면 result에는 작은 노드부터 차례대로 연결된다.

class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        root = result = ListNode(None)
        heap = []
        for i in range(len(lists)):
            if lists[i]:
                heapq.heappush(heap, (lists[i].val, i, lists[i]))
        while heap:
            node = heapq.heappop(heap)
            idx = node[1]
            result.next = node[2]
            
            result = result.next
            if result.next:
                heapq.heappush(heap, (result.next.val, idx, result.next))
        return root.next

PriorityQueue vs heapq

파이썬에서 우선순위 큐는 queue 모듈의 PriorityQueue 클래스를 이용해 사용할 수 있다. 우선순위 큐는 힙을 사용해 주로 구현하고 파이썬의 PriorityQueue조차 내부적으로는 heapq를 사용하도록 구현되어 있다.

PriorityQueue의 _get(), _put()은 모두 heapq 모듈의 heappop(), heappush()를 그대로 이용하기 때문에 사실상 둘은 동일하다고 할 수 있다. 차이점은 스레드 세이프(Thread Safe) 클래스라는 점이고 heapq는 스레드 세이프(Thread Safe)를 보장하지 않는다. 여기서 스레드 세이프는 멀티 스레드에서도 안전한 프로그래밍 개념으로 만약 스레드 세이프하지 않은 경우 1번 스레드의 값이 2번 스레드에서 변경될 수 있어 문제를 발생시키게 된다.

파이썬은 GIL 특성상 멀티 스레딩이 거의 의미 없기 때문에 대부분 멀티 프로세싱으로 활용한다는 점을 생각해보면 PriorityQueue 모듈의 멀티 스레딩 지원은 사실 큰 의미가 없다. 또한 스레드 세이프를 지원한다는 것은 내부적으로 Locking을 제공한다는 의미이므로 Locking Overhead가 발생해 성능에 안좋은 영향을 주게 된다. 따라서 굳이 멀티 스레드로 구현하지 않는다면 PriorityQueue를 사용할 이유가 없다.