슬라이딩 윈도우 (Sliding Window)

슬라이딩 윈도우에 대해 조금 더 알아보았다.

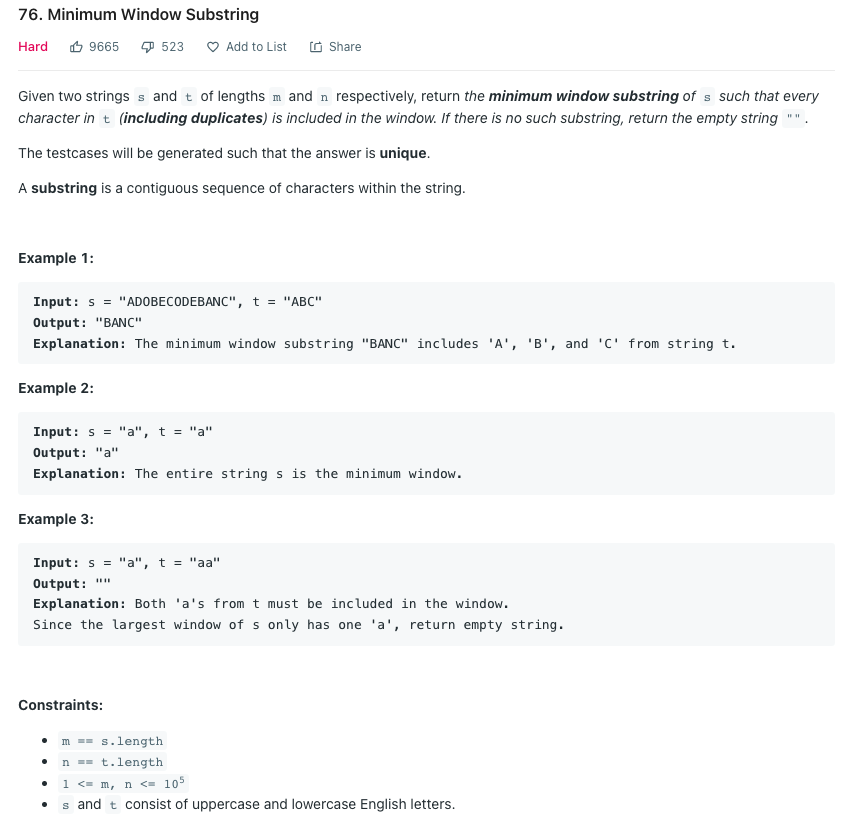
LeetCode 76.Minimum Window Substring

문자열 S와 T를 입력받아 O(n)에 T의 모든 문자가 포함된 S의 최소 윈도우를 찾아라.

Solution 1 모든 윈도우 크기를 브루트 포스로 탐색

먼저 브루트 포스로 풀어보면, 최소 윈도우라고 했으니 일단 T의 크기부터 시작해 점점 크기를 키워가며 모든 윈도우 크기에 대해 탐색해야 한다.

예제에서 T의 크기는 3이므로 먼저 슬라이딩 윈도우 사이즈를 3으로 하고 끝까지 스캔한 후, T에 해당하는 문자열을 발견하지 못한 경우 4, 다시 5, 6...으로 크기를 늘리는 방법을 고민할 수 있다. 이렇게 하면 T 문자열을 가장 먼저 찾게 되는 윈도우 사이즈가 정답이 된다. 그러나 이 문제에서는 시간 복잡도 O(n) 제한이 있기 때문에 O(n^2)인 이 풀이법은 사용할 수 없다.

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        def contains(s_substr_lst: List, t_lst: List):
            for t_elem in t_lst:
                if t_elem in s_substr_lst:
                    s_substr_lst.remove(t_elem)
                else:
                    return False
            return True
        if not s or not t:
            return ''
        window_size=len(t)
        for size in range(window_size, len(s)+1):
            for left in range(len(s)-size+1):
                s_substr=s[left:left+size]
                if contains(list(s_substr), list(t)):
                    return s_substr
        return ''

Solution 2 투 포인터, 슬라이딩 윈도우로 최적화

이런 유형의 문제는 투 포인터를 사용하면 O(n^2)에서 O(n)으로 줄일 수 있다. 계속 우측으로 이동하는 슬라이딩 윈도우이면서 적절한 위치를 찾았을 때 좌우 포인터의 크기를 좁혀 나가는 투 포인터로 풀이할 수 있을 것 같다.

먼저 기본 변수를 다음과 같이 정의한다.

need = collections.Counter(t)
missing = len(t)

need는 필요한 문자 각각의 개수, missing은 필요한 문자의 전체 개수로 한다.

for right, char in enumerate(s, 1):
	missing -= need[char] > 0
    need[char] -= 1
    ...

이제 오른쪽 포인터인 right 값을 계속 늘려 나간다. 슬라이딩 윈도우의 크기가 점점 더 커지는 형태가 된다. 여기서 enumerate(n, 1)은 1부터 시작한다는 의미이다. 파이썬의 슬라이딩은 s[n:n+1]의 형태이므로 오른쪽 포인터인 right는 1부터 시작하게 한다. 만약 현재 문자가 필요한 문자 need[char]에 포함되어 있다면 필요한 문자의 전체 개수인 missing을 1 감소하고, 해당 문자의 필요한 개수 need[char]도 1 감소한다.

if missing == 0:
	while left < right and need[s[left]] < 0:
    	need[s[left]] += 1
        left += 1

missing이 0이 되면, 즉 필요한 문자의 개수가 0이 된다면 이제 왼쪽 포인터를 더 줄일 수 있는지 살핀다. 기준은 음수인 경우이다. 즉 왼쪽 포인터가 불필요한 문자를 가리키고 있따면 분명 음수일 것이고, 0을 가리키는 위치까지 왼쪽 포인터를 이동한다. while 조건문은 wihle left<right and need[s[left]]!=0:으로 해도 동일한 결과가 된다. 다시 슬라이딩 윈도우의 크기가 점점 더 줄어드는 형태가 된다.

if missing==0:
	...
    if not end or right - left <= end - start:
    	start, end = left, right
    need[s[left]] += 1
    missing += 1
    left += 1

그렇게 missing이 0이 될 때까지의 오른쪽 포인터와 need[s[left]]가 0이 될 때까지의 왼쪽 포인터를 정답으로 간주한다. 이 값은 더 작은 값을 찾을 때까지 유지하다가 가장 작은 값인 경우, 정답으로 슬라이싱 결과를 리턴한다. 전체 코드는 다음과 같다.

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        need = collections.Counter(t)
        missing = len(t)
        left = start = end = 0
        for right, char in enumerate(s, 1):
            missing -= need[char] > 0
            need[char] -= 1
            if missing == 0:
                while left < right and need[s[left]] < 0:
                    need[s[left]] += 1
                    left += 1
                if not end or right - left <= end - start:
                    start, end = left, right
                need[s[left]] += 1
                missing += 1
                left += 1
        return s[start:end]

Solution 3 Counter로 좀 더 편리한 풀이

이번에는 필요한 문자의 개수를 직접 계산하지 않고 collections.Counter의 기능을 이용해 매우 편리하게 풀어본다. 같은 방식으로 풀되 missing==0대신 Counter()의 AND 연산으로 다음과 같이 풀 수 있다.

t_count = collections.Counter(t)
...
for right, char in enumerate(s, 1):
	current_count[char] += 1
    while current_count & t_count == t_count:
    	...

지금까지 계산한 current_count와 t_count의 AND 연산으로 모든 결과가 포함되는지 여부를 확인할 수 있다. 만약 요소가 하나라도 비어있다면 AND 연산 결과는 t_count와 일치하지 않을 것이다. 나머지 전체 코드는 이전 풀이와 큰 차이가 없다.

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        t_count = collections.Counter(t)
        current_count = collections.Counter()
        start = float('-inf')
        end = float('-inf')
        left = 0
        for right, char in enumerate(s, 1):
            current_count[char] += 1
            while current_count & t_count == t_count:
                if right - left < end - start:
                    start, end = left, right
                current_count[s[left]] -= 1
                left += 1
        return s[start:end] if end - start <= len(s) else ''

이 풀이는 시간이 매우 오래 걸리는 풀이로 작성은 간단하지만 효율성이 떨어진다. 아마도 Counter끼리 AND 연산으로 비교하는 과정이 내부적으로 매우 무거운 연산이기 때문으로 추측된다. 편리하지만 너무 오래 실행되는 풀이인 만큼, 코딩 테스트나 실무에서는 이런식으로 풀이하긴 어려울 것 같다.

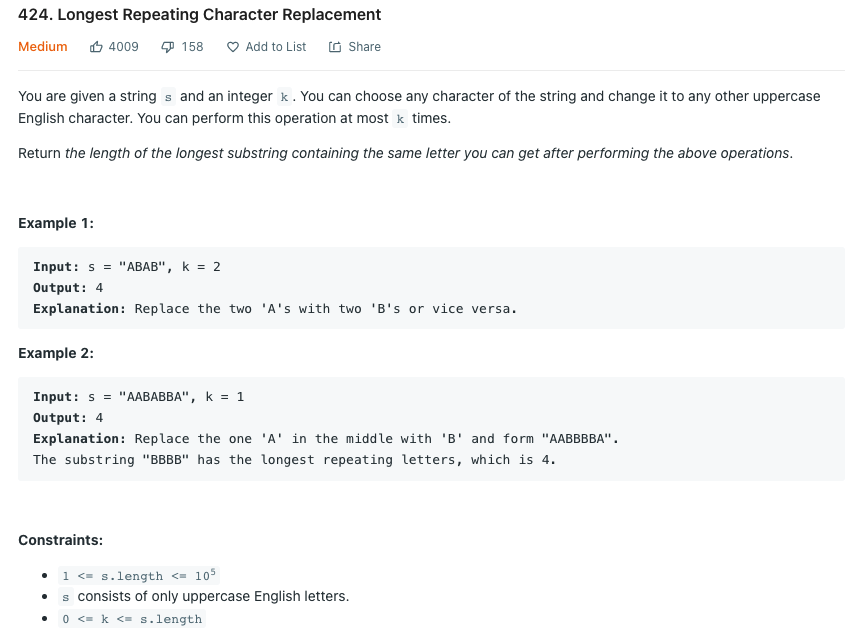
LeetCode 424.Longest Repeating Character Replacement

대문자로 구성된 문자열 s가 주어졌을 때 k번만큼의 변경으로 만들 수 있는, 연속으로 반복된 문자열의 가장 긴 길이를 출력하라.

Solution 1 투 포인터, 슬라이딩 윈도우, Counter를 모두 이용

이 문제는 오른쪽 포인터가 계속 우측으로 이동한다는 점에서 슬라이딩 윈도우 문제이지만 왼쪽 포인터를 계속 좁혀서 범위를 조절해 나간다는 점에서는 76번 문제와 마찬가지로 투 포인터와 결합된 문제로 볼 수 있다.

여러 풀이법 중 최종 결과는 오른쪽 포인터에서 왼쪽 포인터 위치를 뺀 다음, 윈도우 내 출현 빈도가 가장 높은 문자의 수를 뺀 값이 k와 같을 수 있는 수 중 가장 큰 최댓값이라 정의할 수 있다. 이를 코드로 표현해보면 다음과 같다.

max(right) - min(left) - max_char_n == k

최대 길이를 찾는 문제이므로, right는 클수록 좋고, left는 작을 수록 좋다. AAABB라는 문자열이 있을 때 A를 B로 바꾸는 것은 3번, B를 A로 바꾸는 것은 2번의 연산이 필요하다. 따라서 B를 A로 바꾸는 것이 연산 횟수 k를 최소화할 수 있는 방법이며, 이 계산은 마찬가지로 오른쪽 포인터 5에서 왼쪽 포인터 0을 뺀 다음, 출현 빈도가 가장 높은 문자인 A의 개수 3을 뺀 값, 즉 5-0-3이 연산 횟수 k가 되며 이 값은 2가 된다.

left = right = 0
counts = collections.Counter()
for right in range(1, len(s)+1):
	counts[s[right-1]] += 1
    max_char_n = counts.most_common(1)[0][1]
    ...

왼쪽 포인터와 오른쪽 포인터를 0으로 지정한 다음에 오른쪽 포인터 right는 계속 우측으로 한 칸씩 이동한다. 이때 Counter()를 이용해 가장 흔하게 등장하는 문자의 값을 계산해 나간다. 다음 코드를 보면 위의 코들르 이해하기 쉬울 것이다.

>>> counts
Counter({'A': 3, 'B': 2})
>>> counts.most_common()
[('A', 3), ('B', 2)]
>>> counts.most_common(1)
[('A', 3)]
>>> counts.most_common(1)[0]
('A', 3)
>>> counts.most_common(1)[0][1]
3

이 같은 과정을 통해 가장 흔하게 등장하는 문자의 개수를 가져오게 된다. 실행 결과를 하나씩 살펴보면 각 코드가 무엇을 의미하는지 쉽게 이해될 것이다.

if right - left - max_char_n > k:
	counts[s[left]] -= 1
    left += 1

오른쪽 포인터는 계속 커지기 때문에 최댓값을 추출하기 위해서는 왼쪽 포인터는 0에서 움직이지 않는 게 가장 좋다. 그러나 k 연산 횟수를 넘어선다면 어쩔 수 없이 left+=1과 같이 왼쪽 포인터를 1 더 크게 한다. 이제 마지막으로 최대 길이가 되는 값을 찾는다.

max_len = max(right - left, max_len)

오른쪽 포인터에서 왼쪽 포인터를 뺀 값이 가장 긴 길이가 되는 값이다. 즉 맨 처음에 코드로 표현했던 것처럼, 오른쪽 포인터는 가능한 한 크게 하고, 왼쪽 포인터는 가능한 한 작게 하는 값이 된다. 생각해보면 이 부분은 생략이 가능하다. 한번 최댓값이 된 상태에서는 오른쪽 포인터가 한 칸 이동하면ㅇ 왼쪽 포인터도 따라서 이동하게 되면서 max_len값은 바뀌지 않기 떄문이다. 따라서 최댓값을 구하는 부분은 생략할 수 있다. 전체 코드는 다음과 같다.

class Solution:
    def characterReplacement(self, s: str, k: int) -> int:
        left = right = 0
        counts = collections.Counter()
        for right in range(1, len(s) + 1):
            counts[s[right - 1]] += 1
            max_char_n = counts.most_common(1)[0][1]
            if right - left - max_char_n > k:
                counts[s[left]] -= 1
                left += 1
        return right - left

최댓값을 구하는 부분을 생략했기 때문에 얼핏 전체 풀이를 보면 최댓값을 추출하는 결과라는 점을 한 번에 이해하기 어렵다. 가독성이 다소 떨어지는 편이다. 그러나 매번 최댓값을 계산하는 불피룡한 연산을 없앴기 때문에 속도 향상에는 훨씬 더 도움이 된다. 이렇게 가독성과 실행속도는 반비례인 관계가 종종 있으므로 어느 경우를 택하든 많은 고민이 필요하다.