정렬 (Sort)

정렬 알고리즘은 목록의 요소를 특정 순서대로 넣는 알고리즘이다. 대개 숫자식 순서와 사전식 순서로 정렬한다.

버블 정렬 (Bubble Sort)

버블 정렬은 화이트보드 코딩 인터뷰에 자주 등장했던 정렬 알고리즘이다. 비효율적인 정렬 알고리즘이기 때문에 실무에 거의 사용하지 않는다. 따지고 보면 버블 정렬은 전혀 중요한 알고리즘이 아니다. 정렬 자체가 실무와는 거리가 있기도 하지만 그 중에서도 버블 정렬은 더욱 거리가 먼 알고리즘이다.

이 알고리즘은 n번의 라운드로 이뤄져 있으며 각 라운드마다 배열의 아이템을 한 번씩 쭉 모두 살펴본다. 연달아 있는 아이템 2개의 순사가 잘못되어 있는 것을 발견하면, 두 아이템을 맞바꾼다. 배열 전체를 쭉 살펴보는 것을 n번 하기 때문에 시간 복잡도는 항상 O(n^2)이다. 그렇기 때문에 매우 비효율적인 알고리즘이라고 할 수 있다.

def bubblesort(A):
	for i in range(1, len(A)):
    	for j in range(0, len(A)-1):
        	if A[j]>A[j+1]:
            	A[j], A[j+1]=A[j+1], A[j]

매우 간단하게 버블 정렬 알고리즘이 구현되었다.

병합 정렬 (Merge Sort)

병합 정렬은 분할 정복의 진수를 보여주는 알고리즘이다. 최선과 최악 모두 O(n log n)의 시간 복잡도를 가지는 사실상 완전한 O(n log n)으로 일정한 알고리즘이며, 대부분의 경우 퀵 정렬보다는 느리지만 일정한 실행 속도 뿐만 아니라 무엇보다도 안정 정렬이라는 점에서 여전히 상용 라이브러리에 많이 쓰이고 있다.

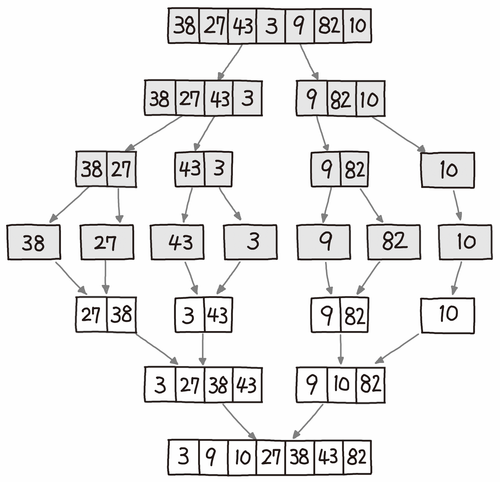
이 그림에서 우리는 분할 정복으로 일정하게 정렬이 이뤄지는 병합 정렬의 특징을 잘 파악할 수 있다. 나눌 수 없을 때까지 두 부분으로 분할한 후에 분할이 끝나면 정렬하면서 정복해 나간다.

def mergesort(A):
    if len(A) < 2:
        return A
    mid = len(A) // 2
    lowA = mergesort(A[:mid])
    highA = mergesort(A[mid:])
    mergedA = []
    l = h = 0
    while l < len(lowA) and h < len(highA):
        if lowA[l] < highA[h]:
            mergedA.append(lowA[l])
            l += 1
        else:
            mergedA.append(highA[h])
            h += 1
    mergedA += lowA[l:]
    mergedA += highA[h:]
    return mergedA

병합 정렬은 위와 같은 형식으로 구현할 수 있다.

퀵 정렬 (Quick Sort)

퀵 정렬은 피벗을 기준으로 좌우를 나누는 특징 떄문에 파티션 교환 정렬이라고도 불린다. 병합 정렬과 마찬가지로 분할 정복 알고리즘이며 여기에 피벗이라는 개념을 통해 피벗보다 작으면 왼쪽, 크면 오른쪽과 같은 방식으로 파티셔닝 하면서 쪼개 나간다. 여러 가지 변형과 개선 버전이 있는데 여기서는 N.로무토가 구현한 파티션 계획을 살펴본다.

우선 파티션을 나누고 각각 재귀 호출하는 전형적인 분할 정복 구조를 먼저 작성하였다.

def quicksort(A, lo, hi):
...
	if lo<hi:
    	pivot=parition(lo, hi)
        quicksort(A, lo, pivot-1)
        quicksort(A, pivot+1, hi)

로무토 파티션은 맨 오른쪽을 피벗으로 정하는 가장 단순한 방식이다. 이를 파이썬으로 구현하면 다음과 같다.

def partition(lo, hi):
	pivot=A[hi]
    left=lo
    for right in range(lo, hi):
    	if A[right]<pivot:
        	A[left], A[right] = A[right], A[left]
            left+=1
	A[left], A[hi] = A[hi], A[left]
    return left

여기서 피벗은 맨 오른쪽 값을 기준으로 하며, 이를 기준으로 2개의 포인터가 이동해서 오른쪽 포인터의 값이 피벗보다 작다면 서로 스왑하는 형태로 진행된다. 이를 도식화하면 다음과 같다.

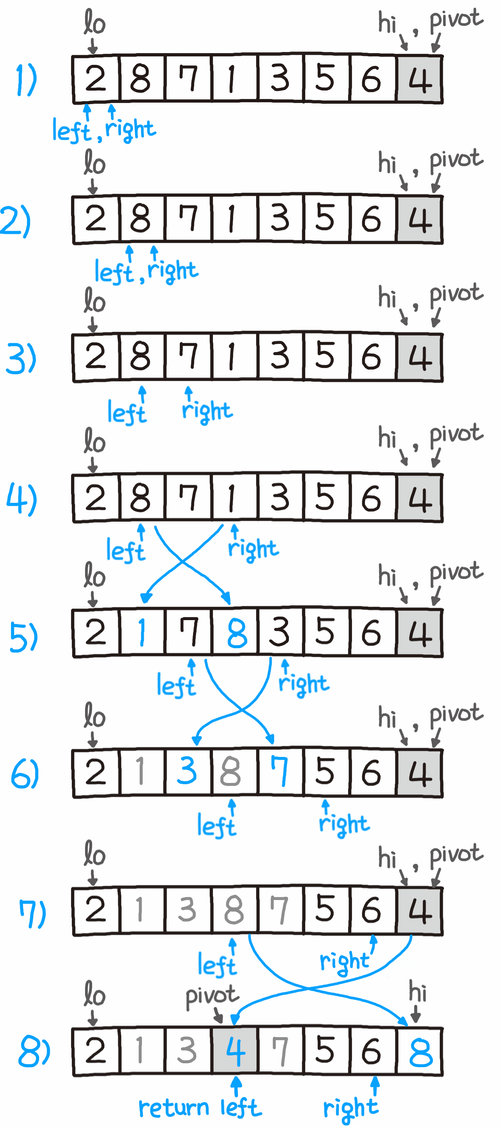
오른쪽 right 포인터가 이동하면서 피벗의 값이 오른쪽 값보다 더 클 때, 왼쪽과 오른쪽의 스왑이 진행된다. 스왑 이후에는 왼쪽 left 포인터가 함께 이동한다. 여기서 피벗의 값은 4이므로, 오른쪽 포인터가 끝에 도달하게 되면 4 미만인 값은 왼쪽으로, 4 이상인 값은 오른쪽으로 위치하게 된다. 그리고 왼쪽 포인터의 위치로 피벗 아이템이 이동한다. 최종 결과인 8)을 보면 4를 기준으로 작은 값은 왼쪽에, 큰 값은 오른쪽에 분할되어 있고, 피벗이 그 중앙으로 이동하는 모습을 볼 수 있다. 이렇게 계속 분할하며 정복을 진행하여 코드 기준으로 lo<hi를 만족하지 않을 때까지, 즉 서로 위치가 역전할 때까지 계속 재귀로 반복되면서 정렬이 완료된다. 정리된 전체 코드는 다음과 같다.

def quicksort(A, lo, hi):
	def partition(lo, hi):
    	pivot=A[hi]
    	left=lo
	    for right in range(lo, hi):
    		if A[right]<pivot:
        		A[left], A[right] = A[right], A[left]
            	left+=1
		A[left], A[hi] = A[hi], A[left]
    	return left
    if lo < hi:
    	pivot = partition(lo, hi)
        quicksort(A, lo, pivot - 1)
        quicksort(A, pivot + 1, hi)

퀵 정렬은 이름처럼 매우 빠르며 굉장히 효율적인 알고리즘이지만 최악의 경우에는 O(n^2)의 시간 복잡도를 가지게 된다. 만약 이미 정렬된 배열이 입력값으로 들어온다면 이 경우 피벗은 계속 오른쪽에 위치하게 되므로 파티셔닝이 전혀 이뤄지지 않게 되고 이때 n번의 라운드를 걸쳐 결국 전체를 비교하기 때문에 버블 정렬과 다를 바 없는 최악의 성능을 보이게 된다. 항상 일정한 성능을 갖는 병합 정렬과 달리 퀵 정렬은 이처럼 입력값에 따라 성능 편차가 심한 편이다.

안정 정렬 vs 불안정 정렬

안정 정렬 알고리즘은 중복된 값을 입력 순서와 동일하게 정렬한다.

퀵 정렬의 또 다른 문제점은 안정 정렬이 아니라는 것이다. 안정 정렬의 경우에는 기존의 시간 순으로 정렬했던 순서를 지역명으로 재정렬하더라도 기존 순서가 그대로 유지된 상태에서 정렬이 이뤄진다. 그러나 불안정 정렬은 시간 순으로 정렬한 값을 지역명으로 재정렬하면 기존의 정렬 순서는 무시된 채 모두 뒤죽박죽 뒤섞인다.

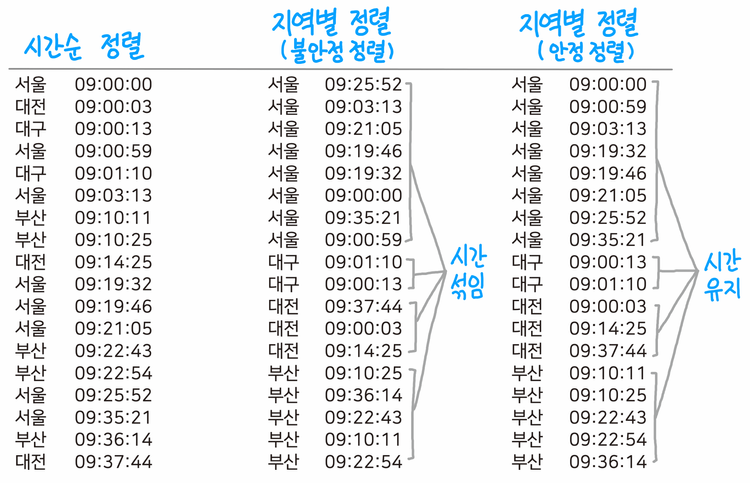
이처럼 입력값이 유지되는 안정 정렬 알고리즘이 유지되지 않는 불안정 정렬 알고리즘보다 훨씬 유용하다는 것은 쉽게 예상할 수 있다.

대표적으로 병합 정렬은 안정 정렬이며, 버블 정렬 또한 안정 정렬이다. 반면 퀵 정렬은 불안정 정렬이다. 게다가 입력값에 따라 버블 정렬 만큼 느려질 수 있다. 이처럼 고르지 않은 성능 탓에 실무에서는 병합 정렬이 여전히 활발히 쓰이고 있으며, 파이썬의 기본 정렬 알고리즘으로 병합 정렬과 삽입 정렬을 휴리스틱하게 조합한 팁소트를 사용한다.