정렬 (Sort)

정렬에 대해 이어서 알아보았다.

LeetCode 179.Largest Number

항목들을 조합하여 만들 수 있는 가장 큰 수를 출력하라.

Solution 1 삽입 정렬

이 문제는 특이한 정렬 기법을 적용해야 한다. 맨 앞에서부터 자릿수 단위로 비교해서 크기 순으로 정렬한다. 즉, 9와 30 중 맨 앞자리가 9가 더 크므로 9가 먼저 나와야 한다. 쉽게 비교하는 방법으로 930과 309를 비교하는 방법이 있다. 이는 다음과 같이 구현할 수 있다.

def to_swap(n1:int, n2:int)->bool:
	return str(n1)+str(n2)<str(n2)+str(n1)

이 함수의 결과가 True일 경우, 위치 변경이 이뤄져야 한다. 배열의 삽입 정렬은 연결 리스트의 삽입 정렬과 다르게 구현된다. 배열의 삽입 정렬 코드는 다음과 같이 구현 가능하다.

def largestNumber(self, nums: List[int])->str:
	i=1
    while i<len(nums):
    	j=i
        while j>0 and self.to_swap(nums[j-1], nums[j]):
        	nums[j], nums[j-1]=nums[j-1], nums[j]
            j-=1
        i+=1
        ...

배열은 이처럼 깔끔하게 구현할 수 있기 때문에 연결 리스트 때처럼 포인터를 맨 앞으로 돌릴지 비교하는 등의 최적화는 수행할 필요가 없다. 아울러 정렬된 리스트 변수를 별도로 선언했던 것과 달리 원래 삽입 정렬을 배열로 구현하게 되면, 이처럼 제자리 정렬이 가능하여 공간 복잡도도 줄일 수 있다. 전체 코드는 다음과 같다.

class Solution:
    @staticmethod
    def to_swap(n1: int, n2:int)->bool:
        return str(n1)+str(n2)<str(n2)+str(n1)
    def largestNumber(self, nums: List[int]) -> str:
        i=1
        while i<len(nums):
            j=i
            while j>0 and self.to_swap(nums[j-1], nums[j]):
                nums[j], nums[j-1]=nums[j-1], nums[j]
                j-=1
            i+=1
        return str(int(''.join(map(str, nums))))

마지막 반환하는 부분이 번잡한 이유는 원래라면 ''.join(map(str, nums))로 끝났겠지만 여기서는 입력값이 ["0", "0"]인 경우도 있기 때문에 그냥 문자로 처리하면 반환값이 00이 되기 때문에 int로 바꿔 00이 0이 되도록 만든 후, 다시 str로 변경하여 그런일을 없앴다.

LeetCode 242.Valid Anagram

t가 s의 애너그램인지 판별하라.

이 문제는 책을 보지 않고 혼자 풀어보았다. 애너그램은 구성하는 문자의 종류와 각 문자의 갯수가 같은 두 문자열을 의미한다. 간단하게 두 문자열을 모두 정렬하고 같다면 True, 다르다면 False를 반환하도록 하였다.

class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        return sorted(s)==sorted(t)

Solution 1 정렬을 이용한 비교

애너그램 여부를 판별하려면 양쪽 문자열을 모두 정렬하고 그 상태가 일치하는지 확인하면 된다. 그냥 두 입력값의 정렬된 결과를 비교하기만 해도 충분하다. 책을 보기 전에 풀었던 코드와 같은 코드가 정답 예시로 등장했다.

class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        return sorted(s)==sorted(t)

LeetCode 75.Sort Colors

빨간색을 0, 흰색을 1, 파란색을 2라 할 때 순서대로 인접하는 제자리 정렬을 수행하라.

Solution 1 네덜란드 국기 문제를 응용한 풀이

이 문제는 다익스트라가 1976년에 제안한 네덜란드 국기 문제와 동일한 문제로 퀵 정렬의 개선 아이디어와 관련 깊다. 네덜란드 국기의 색깔인 붉은색(위), 흰색(중앙), 파란색(아래)을 세 부분으로 대입해 분할하는 것으로서, 피벗보다 작은 부분, 같은 부분, 큰 부분 이렇게 세 부분으로 분할하여 기존 퀵 정렬의 두 부분 분할에 비해 개선하는 방안을 제시하는 것이다.

네덜란드 국기 문제의 수도코드를 코드로 변환하면 이 문제의 정답 코드가 된다. 수도코드는 다음과 같다.

three-way-partition(A: array of values, min: values):
	i <- 0
    j <- 0
    k <- size of A
    
    while j<k:
    	if A[j]<mid:
        	swap A[i] and A[j]
            i <- i+1
            j <- j+1
        else if A[j] > mid:
        	k <- k-1
        	swap A[j] and A[k]
        else:
        	j <- j+1

구성하는 값이 3개 이므로 중간값을 기준으로 하여 중간값보다 작을 경우 앞쪽 인덱스를 채우는 i에 넣고, 중간값보다 클 경우 뒤쪽 인덱스를 채우는 k에 넣고, 중간값인 경우 그대로 두는 방식을 끝까지 이어가게 된다.

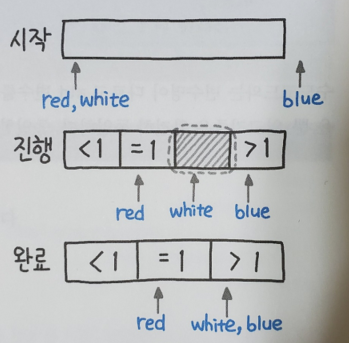
위의 그림은 이 과정을 i는 red, k는 blue, j는 white로 대입하여 도식화한 것이다. 각각의 실제값을 [0, 1, 2]라고 할 때, 비교가 시작되면 1을 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 스왑된다. 이때 red, blue는 간격이 좁아지는 방향으로 이동한다. 투 포인터 풀이와 유사하며, 그 사이에 포인터가 하나 더 존재한다고 볼 수 있다. white와 blue 사이는 계속 비교가 진행된다. 마지막으로 비교가 완료될 때 red는 1보다 작은 인덱스의 +1지점, blue는 1보다 큰 인덱스의 처음을 가리키게 되며, white와 blue가 겹쳐지면서 비교가 완료된다. 이 문제의 정답 코드이자 네덜란드 국기 문제의 코드는 다음과 같다.

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        red, white, blue=0, 0, len(nums)
        
        while white<blue:
            if nums[white]<1:
                nums[red], nums[white]=nums[white], nums[red]
                white+=1
                red+=1
            elif nums[white]>1:
                blue-=1
                nums[white], nums[blue]=nums[blue], nums[white]
            else:
                white+=1

LeetCode 973.K Closest Points to Origin

평면상에 points 목록이 있을 때, 원점 (0, 0)에서 K번 가까운 점 목록을 순서대로 출력하라. 평면상 두 점의 거리는 유클리드 거리로 한다.

이번 문제는 책을 보지 않고 혼자 풀어보았다. 각각의 좌표의 거리를 구한 후, 거리와 그 좌표를 튜플로 묶어 거리 리스트에 저장하고, 거리 리스트를 오름차순 정렬한 후에, k번 정답 리스트에 거리 리스트에 저장된 좌표 두개를 리스트로 만들어 넣어주었다.

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        answers=[]
        dist=[]
        for y, x in points:
            dist.append((y**2+x**2, y, x))
        s_dist=sorted(dist)
        for i in range(k):
            answers.append([s_dist[i][1], s_dist[i][2]])
        return answers

Solution 1 유클리드 거리의 우선순위 큐 순서

유클리드 거리는 유클리드 공간에서 두 점 사이의 거리를 계산하는 가장 일반적인 방법 중 하나로 수식은 √(x1 - x2)^2 + (y1 - y2)^2가 된다. 이 공식을 적용하여 값의 크기가 작은 순으로 K번 추출하면 되는 어렵지 않게 풀 수 있는 문제이다.

K번 추출이라는 단어에서 바로 우선순위 큐를 생각할 수 있다. 즉 유클리드 거리를 계산하고 이 값을 우선순위 큐로 k번 출력하면 쉽게 풀이할 수 있다. math 모듈을 사용해 위의 유클리드 거리 수식을 구현해 계산하고 힙에 삽입하는 코드는 다음과 같다.

heap=[]
for (x, y) in points:
	dist = math.sqrt((0-x)**2 + (0-y)**2)
    heapq.heappush(heap, (dist, x, y))

heapq 모듈을 사용하여 우선순위 큐를 구현했다. 추출을 위한 코드는 다음과 같다.

result=[]
for _ in range(k):
	(dist, x, y) = heapq.heappop(heap)
    result.append((x, y))
return result

결과 리스트에 힙에서 추출한 결과를 k번 삽입해 반환한다.

거리를 구하여 우선순위 큐에 담는 과정에서 실제 거리를 구하고자하는 것이 아니라 단순히 비교만을 위한 것이라면 math.sqrt()를 생략해도 무방하다. 이를 생략한 전체 코드는 다음과 같다.

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        heap = []
        for (x, y) in points:
            dist=x**2 + y**2
            heapq.heappush(heap, (dist, x, y))
        result=[]
        for _ in range(k):
            dist, x, y=heapq.heappop(heap)
            result.append((x, y))
        return result