문제 접근
이 문제는 풀지못하여 좋아하는 이방인님 블로그를 참고하여 제 생각을 정리하였습니다.
출처: https://st-lab.tistory.com/134
몇 가지 조건을 알아보도록 하자.
길이가 3인 계단 수에 대해 구한다면 123, 345 등등이 사용될 것이다.
여기서 123을 살펴보면 3번째 자리의 값은 1, 두 번째 자리는 2, 첫번 째 자리는 3이 될것이다.
다른 조건으로는 인접한 모든 자리의 차이가 1이라는 것인데, 이것을 살펴보면 만약 0일 경우
다음으로는 1 밖에 오지못할 것이다. [-1이 올 수 없기 때문에] 다음으로는 9 다음으로는 8밖에 못 올것이다. [10이 못오기 때문에]
예를 들어 10 다음으로는 101, 89 다음으로는 898 밖에 올 수 없다는 말이다.
나머지 수 2~8 까지는 +1,-1 값을 가질 수 있다.
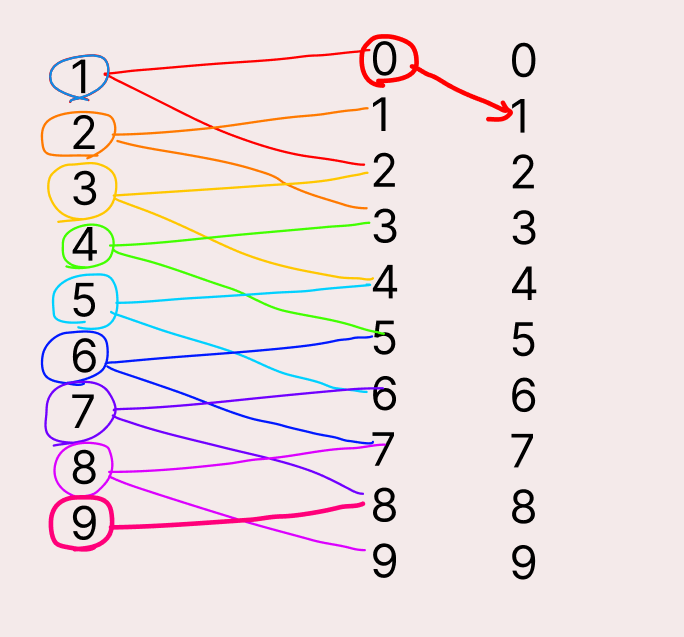
윗 그림은 제가 기억하기 위해 남겨놓습니다...
여기서는 2차원배열을 사용해야 하는데, 2차원 배열을 사용하는 이유는 [N번쨰 자리]의 [자릿값]을 표현하기 위해서 이다.
여기서 N번째 자리는 입력을 받을 것이고 해당 N번 째 자리에 들어가는 값들은 0 ~ 9 까지 일 것이다.
따라서 배열로 표현하면 [Long[N + 1][10]]이다.
여기서 N + 1 인 이유는 인덱스는 0부터 시작이고, 자연수는 1부터 시작이기 떄문이다.
10또한 같은 이유로 9가 아닌 10의 크기를 갖는 것이다.
여기서 헷갈릴 수 있는데, 2차원 배열에서 첫 번째 배열은 자릿수에 해당한다. 아래에서 예를 들어보자
만약 10123 이란 숫자가 있다고 가정할 때
숫자: 1 0 1 2 3
자리: 5번째자리 4번째자리 3.. 2.. 1
이렇게 표현이 가능할텐데, 배열같은 경우 왼쪽에서 오른쪽으로 읽는데, 여기서는 다르게
인덱스를 마치 N번째 자리에 해당하는 값이라고 생각하면 쉽게 이해할 수 있다. 다시말해,
10123일 때
숫자: 1 0 1 2 3
인덱스: 5 4 3 2 1
자리: 5 4 3 2 1
이런식으로 값이 들어가게 된다.
다음으로 1자리만 주어진다면 1 ~9 가 가능하며, 계단 수는 각각 1이 된다.
[1][1] ~ [1][9] = 1;
이제 조건을 가지고 재귀함수를 만든다면 아래와 같을 것이다.
재귀함수는 2가지 인수를 갖는데, 하나는 자릿수에 해당하는 digit과 해당 자리에 할당되어있는 자릿값 val이다.
위에 보았듯이 1자리만 주어졌을 때 1이 모두 할당되었으니 재귀의 종료시점은 digit이 1일 때이다.
private static long recur(int digit, int val) {
if(digit == 1) {
return dp[digit][val];
}
}다음으로는 0과 9에 대한 조건이다. 자리수 N에 대하여 0일 때 뒤에는 1밖에 오지못한다는 점과
9일 때 뒤로는 8밖에 못오는 점이다.
위에서 설명했듯이 이차원배열의 첫 번째 배열은 N번 째 자리를 나타내는 것이다.
예를들어서
숫자: 1 0 1
자리: 3 2 1
인덱스: 3 2 1
따라서 digit - 1를 이해하자면 2째 자리가 0 일때 다음 첫 째 자리로는 1 만 올 수 있기 때문에
digit - 1, 1이 오게되는 것이다.
if(val == 0) {
dp[digit][val] = recur(digit - 1, 1) % mod;
} else if (val == 9){
dp[digit][val]=recur(digit-1, 8) % mod;
}0,9를 제외한 수는 +1, -1를 가질 수 있다.
} else {
dp[digit][val] = (recur(digit - 1, val - 1) + recur(digit - 1, val + 1)) % mod;
}참고한 블로그에서 모듈러연산을 사용하였는데, 모듈러연산에 대해 짧게 설명하자면
% 연산에 대한 나머지 값이 같다는 것이다.
3 % 10 과 13 % 10의 결과 값이 같다는 것이다.
%연산에 대해서 몫은 중요하지 않고, 나머지가 같은 값이 나온다는 것을 설명한다.
A % B 에 대해서 A에 B를 여러번 더해도 같은 결과가 나온다는 것이다.
3 % 10, 13 % 10, 23 % 10 ...,
이것을 가지고 값이 long이 넘어갈 수도 있기 때문에 dp[][]에 저장을 할 때 % mod 만큼하여 저장한다.
결과에서도 % mod한 값을 출력하기 때문이다.
mod값이 10,000일 경우 10,007 % 10,000 에서의 결과는 7이고
7 % 10,000 에서의 결과도 7로 동일하기 때문이다.
전체코드 top-down [재귀]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static Long[][] dp;
static long mod = 1_000_000_000;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
//배열 생성
dp = new Long[N + 1][10];
//초기값 설정
for(int i = 0; i < 10; i++) {
dp[1][i] = 1L;
}
long result = 0;
// N에 도달하기 위한 1 ~9 까지의 수를 구한다.
for(int i = 1; i <= 9; i++) {
result += recur(N, i);
}
System.out.println(result % mod);
}
private static long recur(int digit, int val) {
if(digit == 1) {
return dp[digit][val];
}
if(dp[digit][val] == null) {
if(val == 0) {
dp[digit][val] = recur(digit - 1, 1) % mod;
} else if (val == 9) {
dp[digit][val] = recur(digit - 1, 8) % mod;
} else {
dp[digit][val] = (recur(digit - 1, val - 1) + recur(digit - 1, val + 1)) % mod;
}
}
return dp[digit][val];
}
}
bottom-up
다른 문제로 top-down으로 해결했던 문제를 bottom-up으로 다시 풀어보려 한다.
bottom-up 방식은 아래에서 부터 위로 올라가는 방식으로 초기값 이후 ~ N까지 진행하며 값을 채운다. 따라서, bottom-up 같은경우 이 전 값을 이용하여 현재 dp[] 을 채운다.
다시말해,
N = 3 일때 N < 3 일때의 값을 가지고 N = 3을 채운 다는 것이다.
생각해보면 위의 값은 채워지지 않았기 때문에 이 전값을 사용하는것은 당연한걸지도..?
위에서 볼 수 있듯이 초기값은 1자리 일 경우 1 ~ 9 의 값은 1만 갖는다.
for(int i = 1; i < 10; i++) {
dp[1][i] = 1;
}그리고 조건으로는 만약 현재 자리값의 수가 0 일 때는 1에서 밖에 오지 못 한것이고, 9일때는 8에서 밖에 오지 못한것이다.
그 이외의 숫자 2~8은 다음 자릿수의 +1, -1에서 온 것이다.
if(val == 0) {
dp[digit][val] = dp[digit - 1][1] % mod;
} else if (val == 9) {
dp[digit][val] = dp[digit - 1][8] % mod;
} else {
dp[i][j] = (dp[i - 1][j + 1] + dp[i -1][j - 1]) % mod;
}전체코드 bottom-up
package date_2023_08_15.DP_10844;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static Long[][] dp;
static long mod = 1_000_000_000;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
//배열 생성
dp = new Long[N + 1][10];
//초기값 설정
for(int i = 0; i < 10; i++) {
dp[1][i] = 1L;
}
long result = 0;
bottom_up(N);
for(int i = 1; i <= 9; i++) {
result += dp[N][i];
}
System.out.println(result % mod);
}
static void bottom_up(int N) {
for(int i = 2; i <= N; i++) {
for(int j = 0; j < 10; j++) {
if(j == 0) {
dp[i][j] = dp[i - 1][1] % mod;
} else if (j == 9) {
dp[i][j] = dp[i - 1][8] % mod;
} else {
dp[i][j] = (dp[i - 1][j + 1] + dp[i -1][j - 1]) % mod;
}
}
}
}
}정리
이 문제는 풀면서 처음으로 나온 이차원 배열이다. 여기서 이차원 배열의 개념은 어떠한 N의 자리에 대하여 1~9까지의 값 이었다. 어떠한 N의 자리 / 1 ~ 9 까지의 경우의 수 아직 어떨 때 2차원 배열을 써야하는지 개념이 잡히지 않았지만, 대략 이렇게 이해하고 있다.
이 문제의 경우 예외 조건을 찾는것 또한 중요하다. 곰곰히 생각해보면 어떠한 수 X에 대하여 도달할 수 있는 경우의 수를 찾는 문제였다. 예를 들어, 2자리 3 [2][3] 에 도달하려면 [1][2] 또는 [1][4] 에서
[2][3]에 도달할 수 있는 그런 느낌.. 이랄까.. 거기에 몇 가지 예외를 추가하여 푼 문제 같다.
