[백준] 11726번: 2xn 타일링 - Java, 자바

문제접근

이 문제는 그림을 그려보면 쉽게 해결할 수 있다.
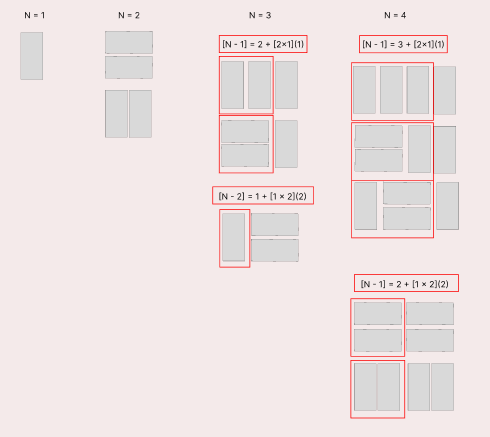
먼저 N = 1 일때는 방법의 수는 1개이다. 2 x1 로 채울수 있는 방법은 세로 타일 하나만 가능하기 때문이다.
두 번째로 N = 2 일때는 2가지 방법이 있다. 가로 타일 2개 또는 세로 타일 2개
여기서 부터 중요하다.
N = 3 일 때를 살펴보면 N = 2 일때의 타일에 세로 타일을 하나 추가한 방법의 수 + N = 1 일때의 타일에 가로 타일 2개를 추가한 방법의 수를 합한 방법의 수와 같다.
다음으로 N = 4 일때를 살펴보면 동일하게 N = 3 일때의 방법의 수에 세로 타일을 하나 추가하 방법의 수 +
N = 2 일때의 방법의 수에 가로 타일 2개를 합한 방법의 수와 같다.

어떻게 규칙을 찾을 수 있었을까?

생각해보면 간단하다. N = 1[2 x 1 (가로1칸)] 일때 타일의 방법의 수는 가로 1칸을 채울 수 있는 방법 1개만 존재한다.
다음으로 N = 2[2 x 2(가로2칸)] 일때를 확인하면 가로 2칸을 채울 수 있는 세로타일 2개 또는 가로타일 2개이다.
N = 3 [2 x 3(가로3칸)] 일 때 가로 3칸을 채울 수 있는 방법을 생각해보면 N = 2 (가로2칸) 에 가로 1칸을 채울 수 있는 세로 타일을
붙이게 되면 [2 x 3]을 채울 수 있다. 또 다른 방법으로 [2 x 3] 칸을 채울 수 있는 방법은 N = 1일때 (가로1칸)을 가로 2칸을 채울 수 있는
가로 타일을 2개 붙이게 되면 [2 x 3] 을 채울 수 있다.
N = 4[2 x 4 (가로4칸)]도 위와 동일하게 N = 3 (가로3칸)에 가로 1칸을 채울 수 있는 세로 타입을 붙이게 되면 된다. 또 다른 방법으로는 N = 2(가로2칸)일 때에
가로 2칸을 채우면 [2 x 4] 를 채울 수 있다. 이러한 규칙을 보면 아래와 같은 점화식을 세울 수 있다.
T[N] = T[N - 1] + T[N - 2].

전체코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

    static Integer[] dp;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        dp = new Integer[N + 1];
        dp[0] = dp[1] = 1;

        System.out.println(recur(N));
    }

    private static int recur(int n) {
        if(dp[n] == null) {
            dp[n] = (recur(n - 1) + recur(n - 2)) % 10007;
        }
        return dp[n];
    }
}

코드 상세

• N을 입력받는다.
• memoization을 위해 static 영역에 dp[]을 만든다.
  • 크기가 N + 1인 이유는 입력값이 1 ~ 1000인데, 인덱스 값은 0부터 시작이기때문에 + 1을 해준다.

static Integer[] dp;

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
dp = new Integer[N + 1];

• 다음으로는 초기값을 설정한다.
  • dp[0] = dp[1] = 1;
    • 여기서 dp[2] = 2;를 하지 않는 이유는 아래와같다.
    • 1<=N<= 1000 인 상황에서 n = 1을 입력하면 dp배열의 크기는 2가 된다.
    • 다시말해 index =0, index = 1; 에만 접근이 가능하다 하지만 이 상황에 dp[2]를
    • 접근하려 할 때 범위에 벗어나는 index에 접근하려 하니 오류가 발생하기 때문이다.

dp[0] = dp[1] = 1;

• dp 배열에 값을 담을 재귀함수를 호출한다.

System.out.println(recur(N));


private static int recur(int n) {
    if(dp[n] == null) {
        dp[n] = (recur(n - 1) + recur(n - 2)) % 10007;
    }
    return dp[n];
}

정리

이 문제도 dp[N]을 채우는 규칙을 찾아 넣는문제였다.
다시말해, N에 도달하기 위한 규칙을 찾는 문제였다.
이렇게 무언가 그림으로 해결할 수 있는 문제는 손으로 직접 그려가며 규칙을 찾아내는 것이 도움이된다.