[백준] 1912번: 연속합 - Java, 자바

문제접근

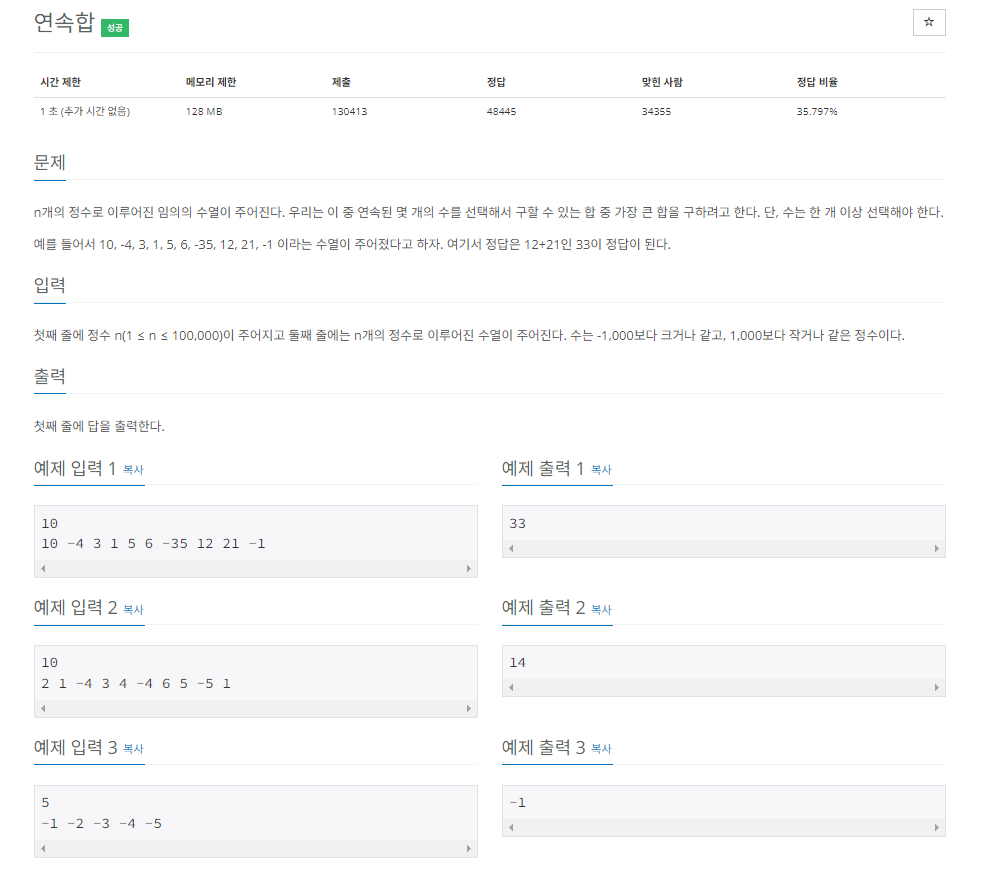
이 문제는 손으로 써보면 쉽게 해결할 수 있는 문제이다.
이 문제의 핵심은 연속된 몇 개의 수를 합하여 가장 큰 합을 구하는 것이다.
맨 처음 이 문제를 풀 떄 수열로 헷갈려서 문제를 틀렸는데, 잘 읽어보면 연속된 몇 개의 수에 답이 있다.
0부터 N까지 수를 합하면서 현재 [자기자신] 과 [이 전까지 합한 수 + 자기자신]을 비교하여 큰 값을 dp에 저장하면 된다.
예를들어서 예제 입력
10 -4 3 1 5 6 -35 12 21 -1

• idx[0] = 10;
  • idx[0] 이전 값을 비교할 것이 없기 때문에 자기자신 10이 가장 크다.
  • dp[0] = 10;
• idx[1] = -4; [이전 값 = 10]+ [자기자신 = -4] = [6];
  • idx[1]은 -4 이지만 이전 값 10을 합치면 6으로 자기자신보다 크다.
  • dp[1] = dp[0] + idx[1] = 6;
• idx[2] = 3;
  • idx[2]는 비교할 것 없이 이전 값과 자신을 합한 값이 크다.
  • dp[2] = dp[1] + idx[2] = 9;
• idx[3] = 1;
  • idx[3]도 동일하다
  • dp[3] = dp[2] + idx[3] = 10;
• idx[4] = 5;
  • idx[4]도 동일하다
  • dp[4] = dp[3] + idx[4] = 15;
• idx[5] = 6;
  • idx[5] 도 동일하다
  • dp[5] = dp[4] + idx[5] = 21;
• idx[6] = -35;
  • idx[6]은 음수인데, 자기자신 보다는 자기자신의 값 + 이전 합한 값을 합친 값이 더 크다.
  • 즉, dp[6] = dp[5] + idx[6] = -14;
• idx[7] = 12;
  • idx[7]은 이전값 + 자기자신 보다 자기자신의 수가 더 크다는 것을 한눈에 알 수 있다.
  • 여기에서는 이 전까지 합한 값을 버리게 되며, dp[7]에는 idx[7] 자기자신만 들어가게 된다.
  • dp[7] = idx[7] = 12;
• idx[8] = 21;
  • idx[8]에서는 이전 값 dp[7]과 자기자신을 합한 값이 크다는것을 알 수 있다.
  • dp[8] = dp[7] + idx[8] = 33;
• idx[9] = -1;
  • idx[9] 도 dp[8]과 자기자신을 합한 값이 더 크다.
  • dp[9] = dp[8] + idx[9] = 32;

이제 dp[]의 값을 모아보면 아래와 같다.
[10, 6, 9, 10, 15, 21, -14, 12, 33, 32]
여기서 가장 큰 수는 33이다. 33 = dp[8] 은 idx[7], idx[8]을 합친 값이란걸 알 수 있다.
이것을 코드로 보자면

전체코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    static Integer[] dp;
    static int[] numbers;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        dp = new Integer[N];
        numbers = new int[N];

        for(int i = 0; i < N; i++) {
            numbers[i] = Integer.parseInt(st.nextToken());
        }

        dp[0] = numbers[0];


        recur(N - 1);



        int max = Integer.MIN_VALUE;

        for(int i = 0; i < N; i++) {
            max = Math.max(max, dp[i]);
        }

        System.out.println(max);


    }


    static int recur(int N) {

        if(dp[N] == null) {
            dp[N] = Math.max(recur(N - 1) + numbers[N], numbers[N]);
        }

        return dp[N];
    }
}

코드 상세

top-down

위에서 아래로 진행하며 자기자신의 값과 |이전 dp[]의 값 + 자기자신| 을 비교하여 더 큰 값을 dp[]에 넣는다.

recur(N - 1);

static int recur(int N) {

    if(dp[N] == null) {
        dp[N] = Math.max(recur(N - 1) + numbers[N], numbers[N]);
    }

    return dp[N];
}

• N을 입력받아 dp[], numbers[]을 초기화한다.
• 다음으로 입력받는 수열을 numbers 배열에 저장한다.

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

int N = Integer.parseInt(br.readLine());

StringTokenizer st = new StringTokenizer(br.readLine(), " ");

dp = new Integer[N];
numbers = new int[N];

for(int i = 0; i < N; i++) {
    numbers[i] = Integer.parseInt(st.nextToken());
}

• dp[0]의 값을 초기화해준다.
  • dp[0]의 값은 이전 값과 비교할 값이 없기 때문에 number[0]의 값을 갖는다.

dp[0] = numbers[0];

• N - 1 부터 재귀를 호출하여 dp배열을 초기화한다.

recur(N - 1);

static int recur(int N) {

    if(dp[N] == null) {
        dp[N] = Math.max(recur(N - 1) + numbers[N], numbers[N]);
    }   

    return dp[N];
}

• dp배열 중 가장 큰 값을 출력한다

int max = Integer.MIN_VALUE;

for(int i = 0; i < N; i++) {
    max = Math.max(max, dp[i]);
}

System.out.println(max);