[Data Structure] #이진 탐색 트리(Binary Search Tree)

이진 탐색트리는 이진트리를 기반으로 탐색을 위한 자료구조입니다. root노드보다 작은 경우 왼쪽 서브트리, 큰 경우 오른쪽 서브트리의 노드로 위치합니다.

시간복잡도

최악의 경우 = O(N)

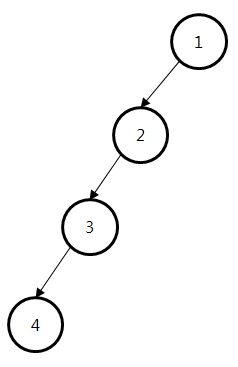
서브트리가 한 쪽만 있는 경우가 최악의 경우이며 이때의 시간복잡도는 O(n)에 해당됩니다.

평균 = O(logN)

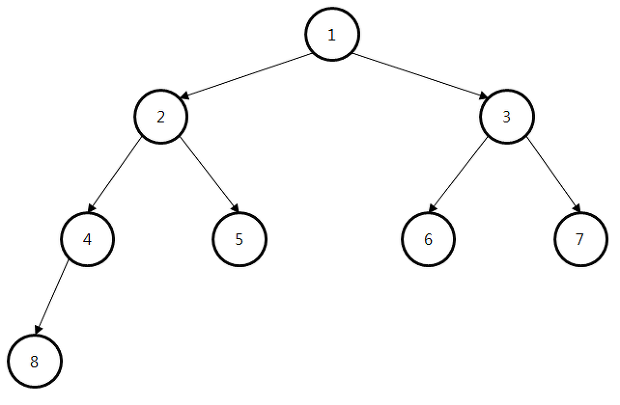
이진 탐색트리에서 탐색, 삽입, 삭제 연산의 시간복잡도는 높이를 h라 했을때 O(h)입니다. 노드가 n일 경우 h=log2n이며 따라서, 시간복잡도는 O(logn)입니다.

구현

탐색

탐색은 순환, 반복 두가지 방식으로 구현해봤습니다.

순환

TreeNode* search_recursion(TreeNode *node, int data) {
  if (node == NULL) return NULL;
  if (node->data == data) return node;
  if (node->data < data) { 
    return search(node->right, data)
  } else {
    return search(node->left, data);
  }
}

반복

// 반복을 활용한 search 알고리즘
TreeNode* search_interation(TreeNode *node, int data) {
  while(node != NULL) {
    if (node->data == data) return node;
    if (node->data > data) {
      node = node->left;
    } else {
      node = node->right;
    }
  }
  return NULL;
}

삽입

TreeNode* create_node(int data) {
  TreeNode* new_node = (TreeNode*)malloc(sizeof(TreeNode));
  new_node->data = data;
  new_node->left = NULL;
  new_node->right = NULL;
  return new_node;
}

TreeNode* insert_recursion(TreeNode *node, int data) {
  if (node == NULL) return create_node(data);

  /**
   * 단말노드인 경우 메모리를 할당해서 새로운 노드를 만든 후에 포인터로 연결한다.
   * 그렇지 않은경우 insert_recursion은 node를 반환하므로 기존에 연결된 포인터를 유지한다.
  **/
  if (data < node->data) {
    node->left = insert_recursion(node->left, data); 
  } else if (data > node->data) {
    node->right = insert_recursion(node->right, data);
  }

  return node;
}

삭제

이진 탐색트리에서 삭제 연산을 잘 봐야합니다. 이 부분이 꽤 복잡한데 다른 연산과는 다르게 삭제 연산은 케이스를 분기처리해줘야합니다.

• 단말 노드를 삭제하려는 경우 : 부모 노드의 포인터를 NULL로 만든다.

• 삭제하려는 노드가 하나의 서브트리만 가지는 경우: 하나의 서브트리만 가지므로 그냥 한 다리 건너서 링크를 연결해주면 된다.

• 삭제하려는 노드가 두개의 서브트리를 가지는 경우: 이 경우에는 후계자로 될 수 있는 노드가 2가지이다. 하나는 왼쪽 서브트리에서 가장 큰 값, 하나는 오른쪽 서브트리에서 가장 작은 값을 가지는 노드이다.따라서 후계자 노드를 탐색하는 과정이 추가된다.

분기처리에서는 1,2케이스를 같은 분기로 처리합니다. 코드를 확인하세요.

TreeNode* delete_recursion(TreeNode *root, int data) {
  if (root == NULL) return root;

  if (data < root->data) {
    root->left = delete_recursion(root->left, data)
  } else if (data > root->data) {
    root->right = delete_recursion(root->right, data)
  } else { // 탐색 성공했을 경우 세가지 케이스에 대해 핸들링한다.
    if (root->left == NULL) {
      TreeNode *temp = root->right;
      free(root);
      return temp;
    } else if (root->right == NULL) {
      TreeNode *temp = root->left;
      free(root);
      return temp;
    } 

     TreeNode *temp = min_value(root->right);
     root->data = temp->data;

     delete_recursion(root->right, temp->data);
  }

  return root;
}

TreeNode* min_value(TreeNode *root) {
  TreeNode *current = root;

  while(current->left != NULL) {
    current = current->left;
  }

  return current;
}