여러 카메라 뷰를 통해 얻은 이미지에서 3차우너 공간의 구조를 추론하는 이론이다.
Projective space
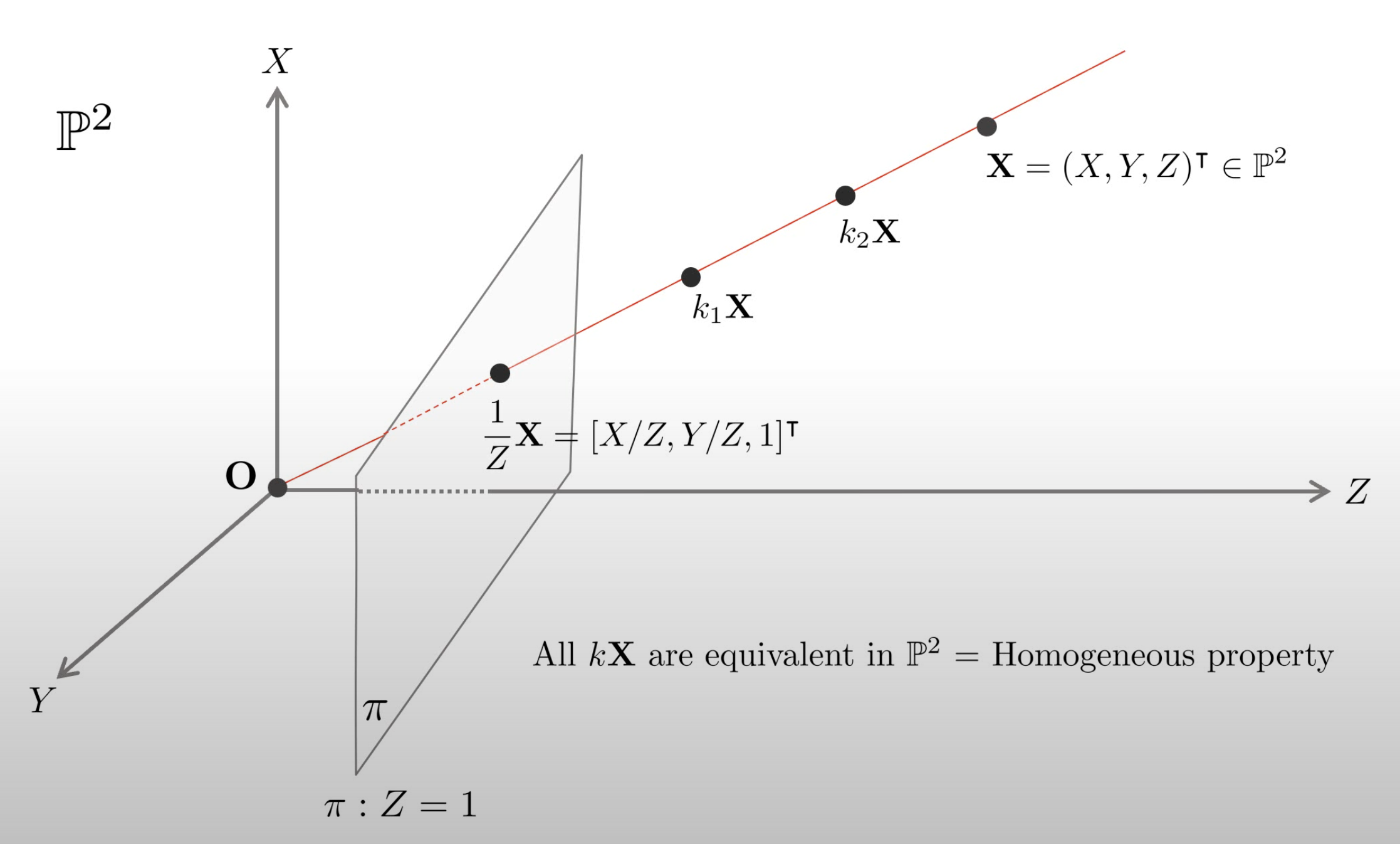
R P n = R n + 1 − { 0 } \mathbb{R}\mathbb{P}^{n} = \mathbb{R}^{n+1} - \{0\} R P n = R n + 1 − { 0 } 사영공간 P n \mathbb{P}^{n} P n R n + 1 \mathbb{R}^{n+1} R n + 1 R n + 1 \mathbb{R}^{n+1} R n + 1 R P n \mathbb{R}\mathbb{P}^{n} R P n
3차원 공간상의 점들을 특정 평면 위에 프로젝션하여 R 2 \mathbb{R}^2 R 2
반대로 생각하면, 이미지에 존재하는 픽셀은 원점에서 나오는 ray 상의 모든 점에 매칭될 수 있다.
점과 직선을 3차원 벡터로 연산할 수 있기 때문에 SLAM을 하는데 있어 많은 이점을 갖는다.
Homogeneous presentation of line
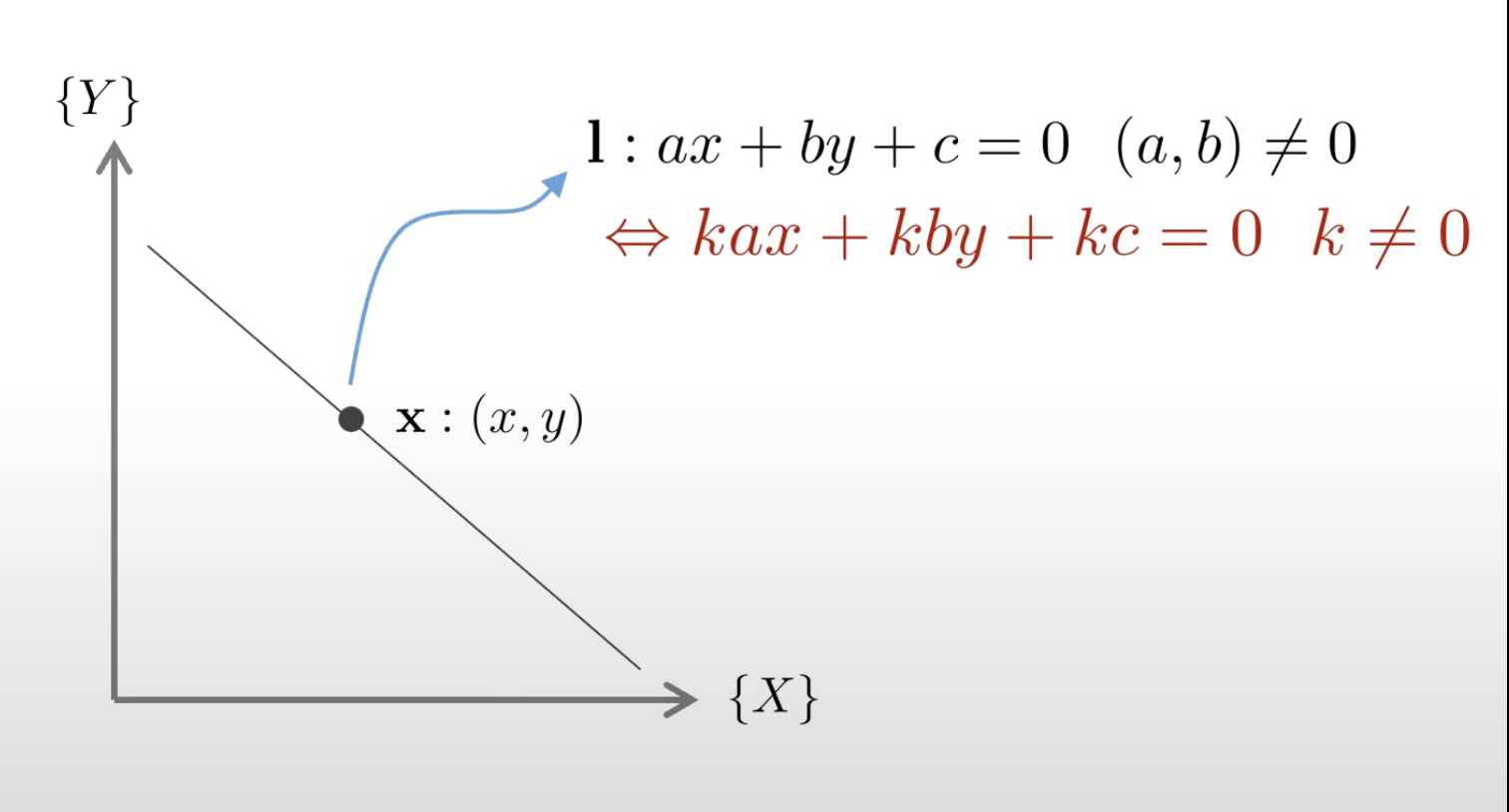
평면위의 점은 x = ( x , y ) ∈ R 2 x=(x,y) \in \mathbb{R}^2 x = ( x , y ) ∈ R 2 l : a x + b y + x = 0 , ( a , x ) ≠ 0 l:ax+by+x=0,(a,x)\neq0 l : a x + b y + x = 0 , ( a , x ) = 0
l : k a x + k b y + k x = 0 l:kax+kby+kx=0 l : k a x + k b y + k x = 0 ( k a , k b , c ) = ( a , b , c ) (ka,kb,c) = (a,b,c) ( k a , k b , c ) = ( a , b , c ) 또한 직선은 선형대수의 파라미터 관점에서 l : ( a , b , c ) l:(a,b,c) l : ( a , b , c )
따라서 평면위의 직선 l l l k k k
Homogeneous presentation of point
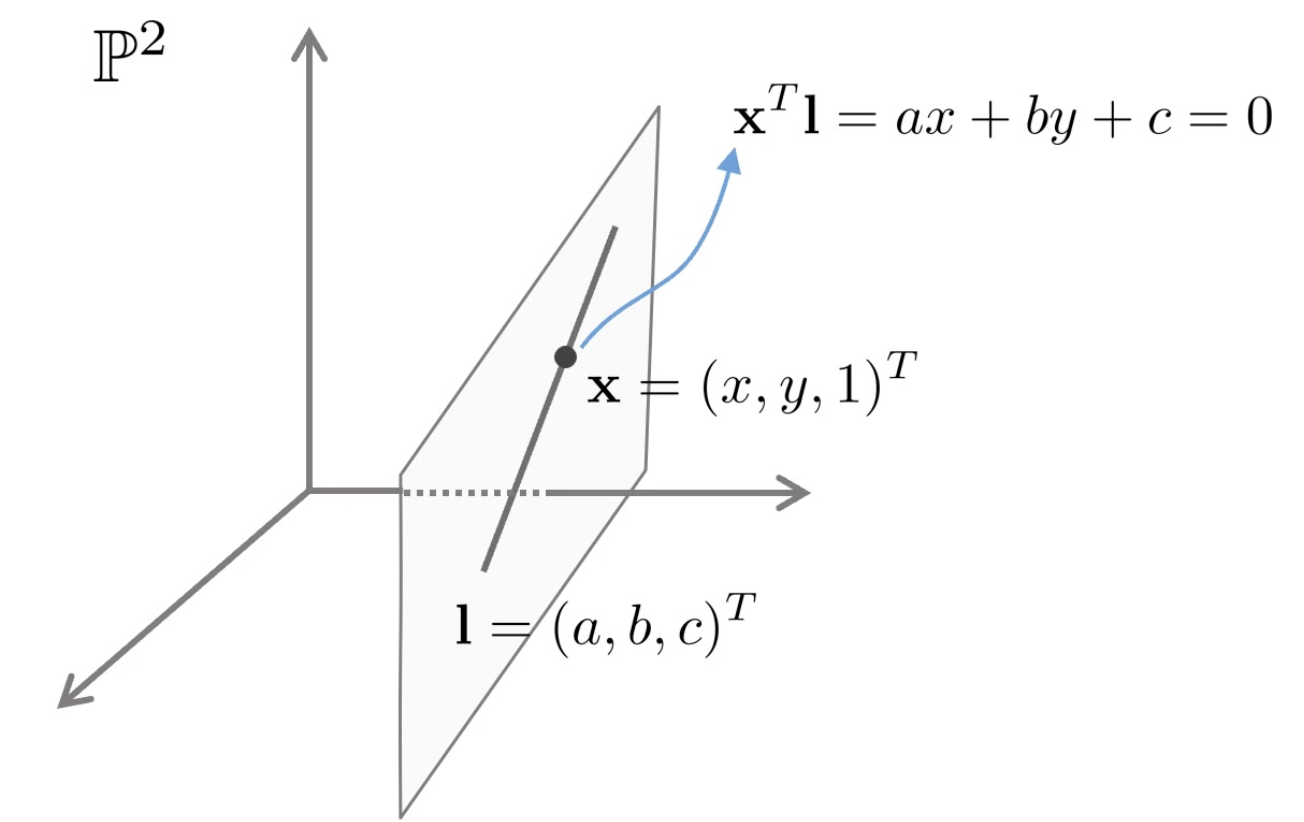
직선 l : ( a , b , c ) T l:(a,b,c)^{T} l : ( a , b , c ) T x = ( x , y ) T x=(x,y)^{T} x = ( x , y ) T
x T l = [ x y 1 ] [ a b c ] = [ x y 1 ] l = 0 x^Tl= \begin{bmatrix}x&y&1 \end{bmatrix} \begin{bmatrix} a\\b\\c\end{bmatrix} = \begin{bmatrix}x&y&1 \end{bmatrix}l = 0 x T l = [ x y 1 ] ⎣ ⎢ ⎡ a b c ⎦ ⎥ ⎤ = [ x y 1 ] l = 0
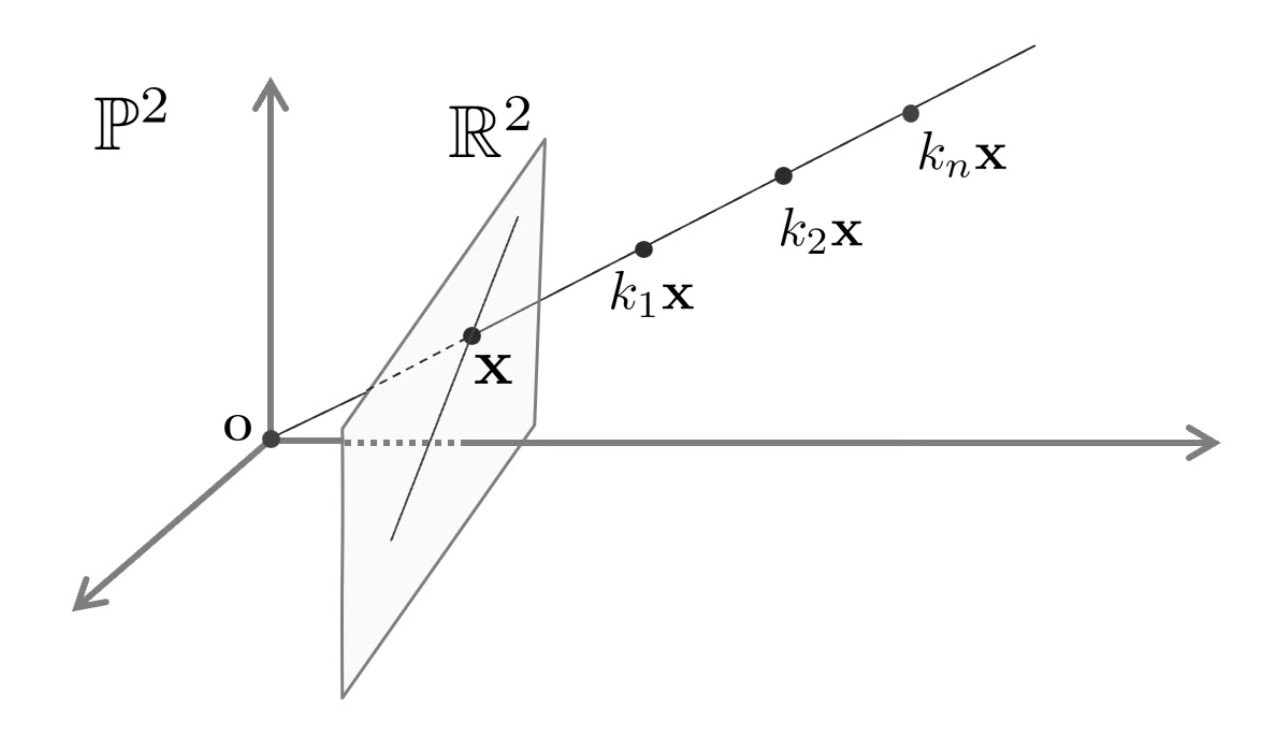
한 점과 그 점을 지나는 직선은 내적했을 때 0이 되는 것을 볼 수 있다. 직선 l l l k k k
k x T l = [ k x k y k ] [ a b c ] = [ k x k y k ] l = 0 kx^Tl= \begin{bmatrix}kx&ky&k \end{bmatrix} \begin{bmatrix} a\\b\\c\end{bmatrix} = \begin{bmatrix}kx&ky&k \end{bmatrix}l = 0 k x T l = [ k x k y k ] ⎣ ⎢ ⎡ a b c ⎦ ⎥ ⎤ = [ k x k y k ] l = 0 Duality of points and lines
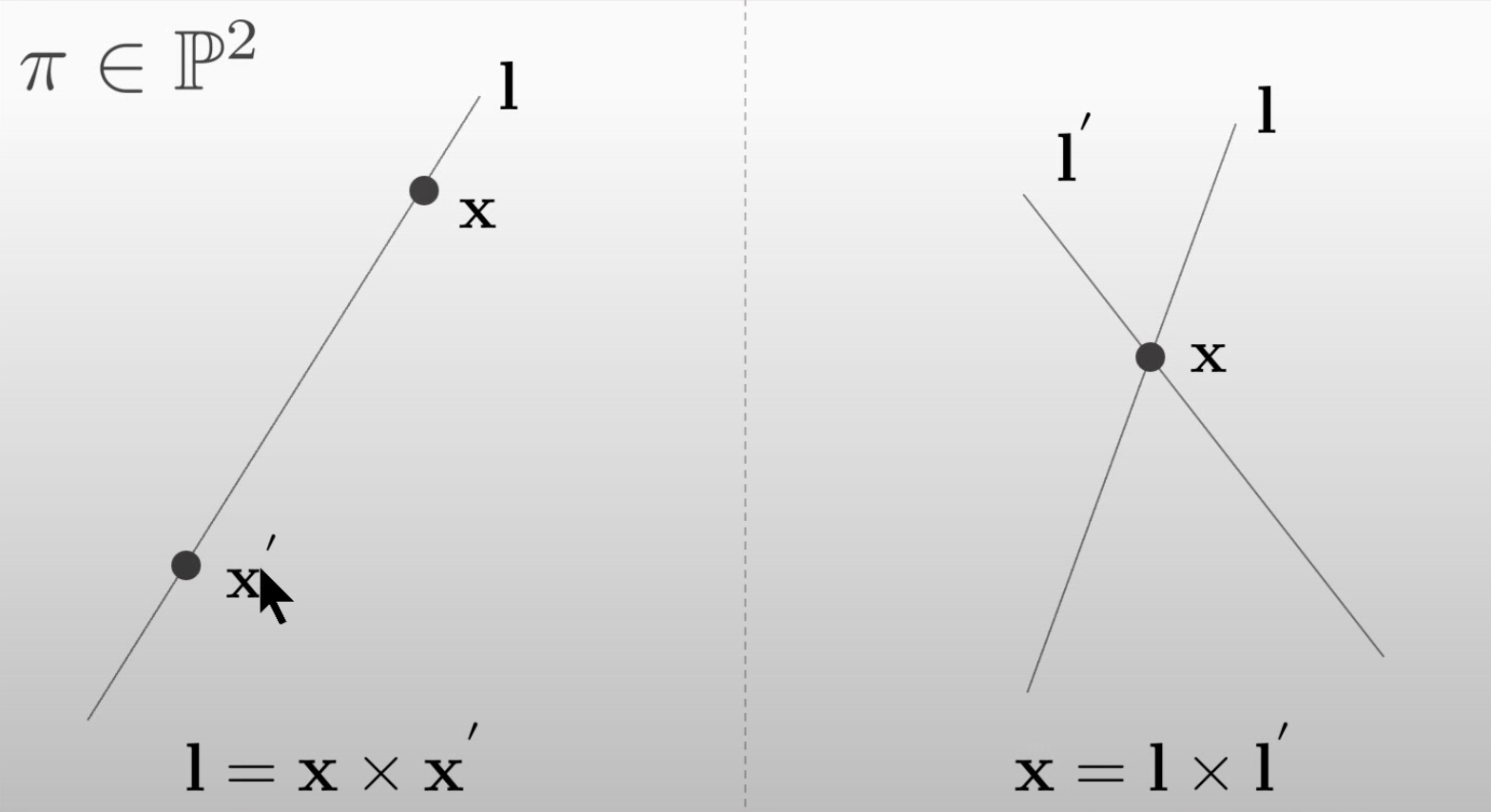
x = l × l ′ l = x × x ′ x=l\times l^\prime \\ l=x\times x^\prime x = l × l ′ l = x × x ′ P 2 \mathbb{P}^2 P 2
P 2 \mathbb{P}^2 P 2 3 × 3 3\times3 3 × 3 H H H P 2 → P 2 \mathbb{P}^2 \rightarrow \mathbb{P}^2 P 2 → P 2
Isometry
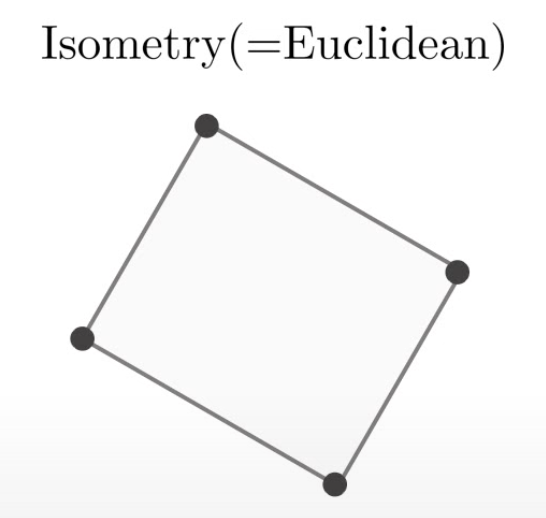
물체의 회전과 평행 이동을 정의하는 변환 행렬이다. 물체의 크기는 보존된다. A는 2차원에 대한 회전행렬로 물체의 회전을 t는 2차원 벡터로 평행 이동을 표현한다.
H i s o = [ A t 0 1 ] ∈ R 3 × 3 H_{iso} = \begin{bmatrix} A&t\\0&1 \end{bmatrix} \in R^{3\times3} H i s o = [ A 0 t 1 ] ∈ R 3 × 3 Similarity
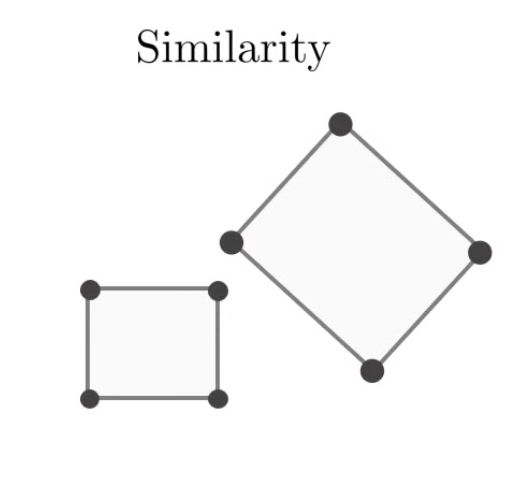
Isometry 변환에 스케일 상수 s가 추가된 변환을 의미한다. 물체의 각도와 길이의 비율은 보존 되지만 크기는 보존되지 않는 변환을 의미한다.
H s = [ s A t 0 1 ] ∈ R 3 × 3 H_{s} = \begin{bmatrix} sA&t\\0&1 \end{bmatrix} \in R^{3\times3} H s = [ s A 0 t 1 ] ∈ R 3 × 3 Affine
Isometry 변환에 A 행렬에 아무런 조건이 없는 변환행렬을 의미한다. 변환 후 물체는 일반적으로 변환 전과 다른 형태를 갖는다. 평행한 직선은 보존하는 성질을 갖는다.
H A = [ A t 0 1 ] ∈ R 3 × 3 H_{A} = \begin{bmatrix} A&t\\0&1 \end{bmatrix} \in R^{3\times3} H A = [ A 0 t 1 ] ∈ R 3 × 3 Projective
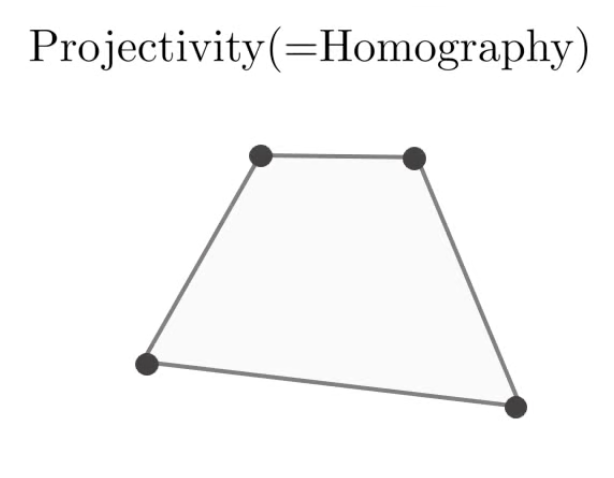
Isometry 변환에 마지막 행이 [ 0 0 1 ] \begin{bmatrix} 0&0&1 \end{bmatrix} [ 0 0 1 ]
H P = [ A t V T v ] ∈ R 3 × 3 H_{P} = \begin{bmatrix} A&t\\V^{T}&v \end{bmatrix} \in R^{3\times3} H P = [ A V T t v ] ∈ R 3 × 3 Pinhole camera model
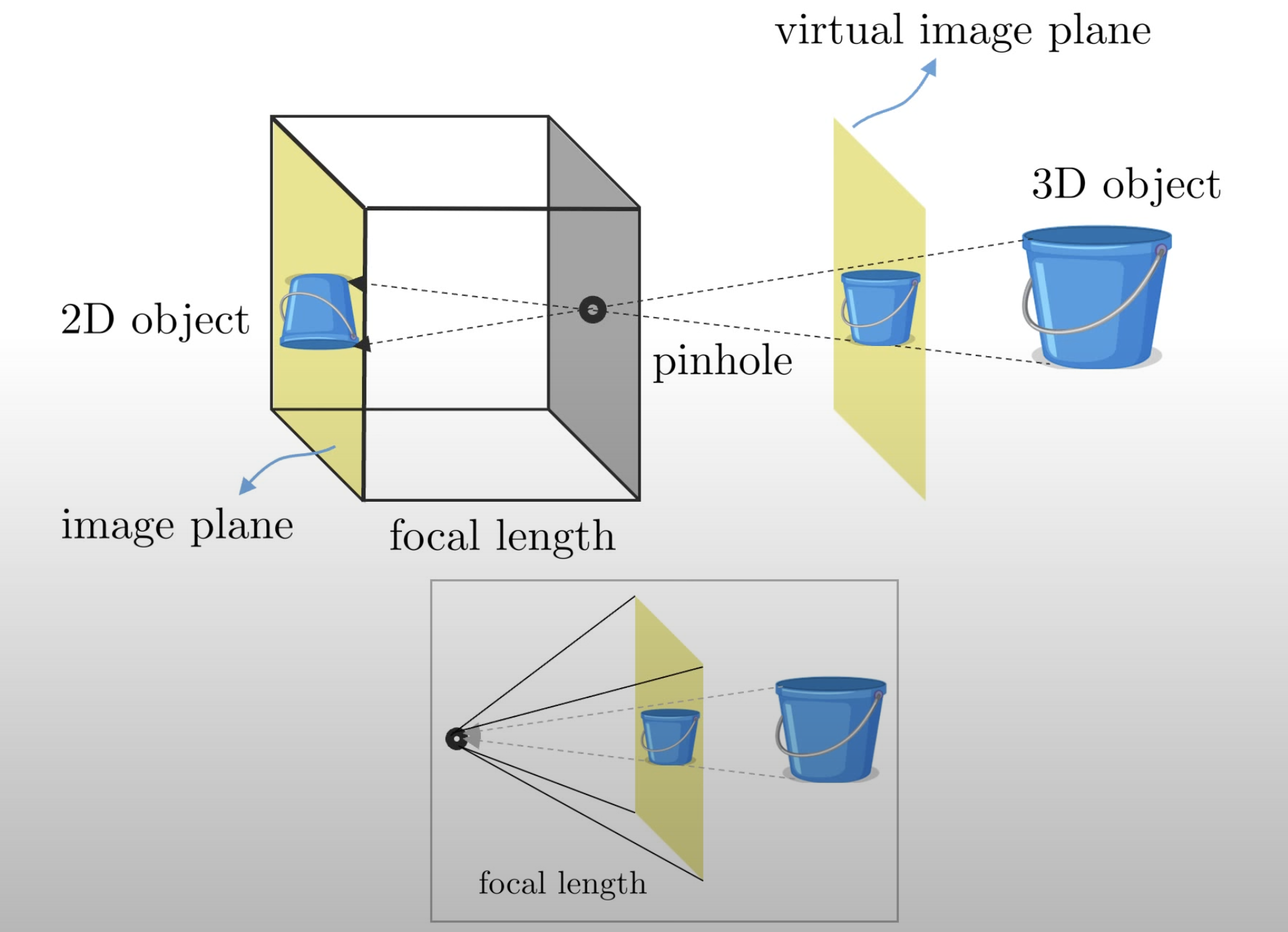
카메라가 작은 구멍(pinhole)을 통해 3차원 물체를 2차원 이미지로 매핑하는 수학적 카메라 모델링 방법이다. 수학적 카메라 모델링 방법 중 개념이 가장 직관적이고 비교적 연산이 단순하기 때문에 보편적으로 사용되는 모델링 방법이다.
계산의 편의를 위해 일반적으로 가상의 이미지 평면을 앞에 위치시켜 해석한다. 실제 카메라의 경우 이미지를 상하좌우를 반적시키지만 이를 영상으로 받아오는 과정에서 역순으로 읽음으로써 우리가 보는 일반적인 영상으로 확인이 가능하다.
카메라의 정면을 z축으로 직교 좌표계로 표현이 가능하다.
Compute 2D point from 3D point
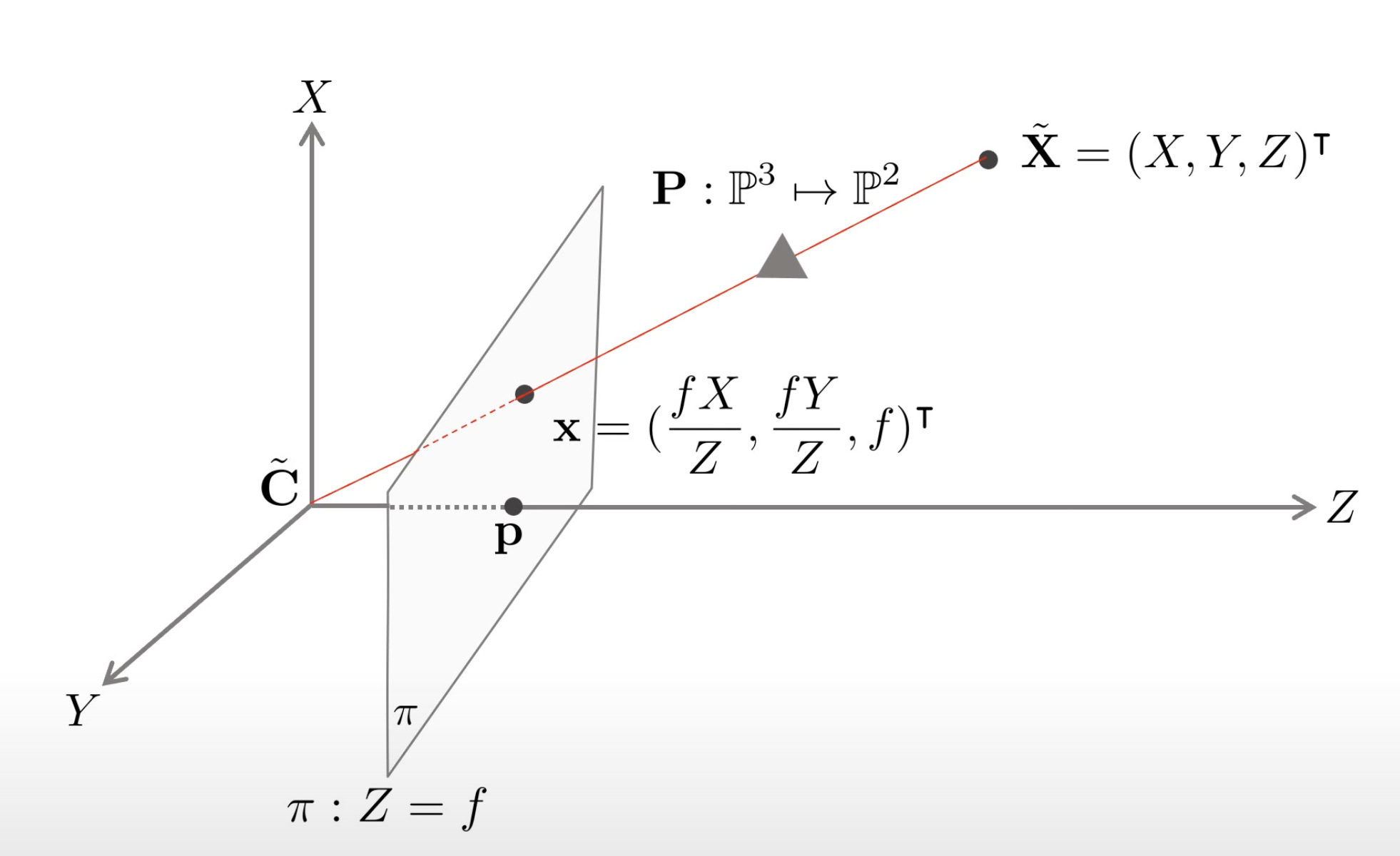
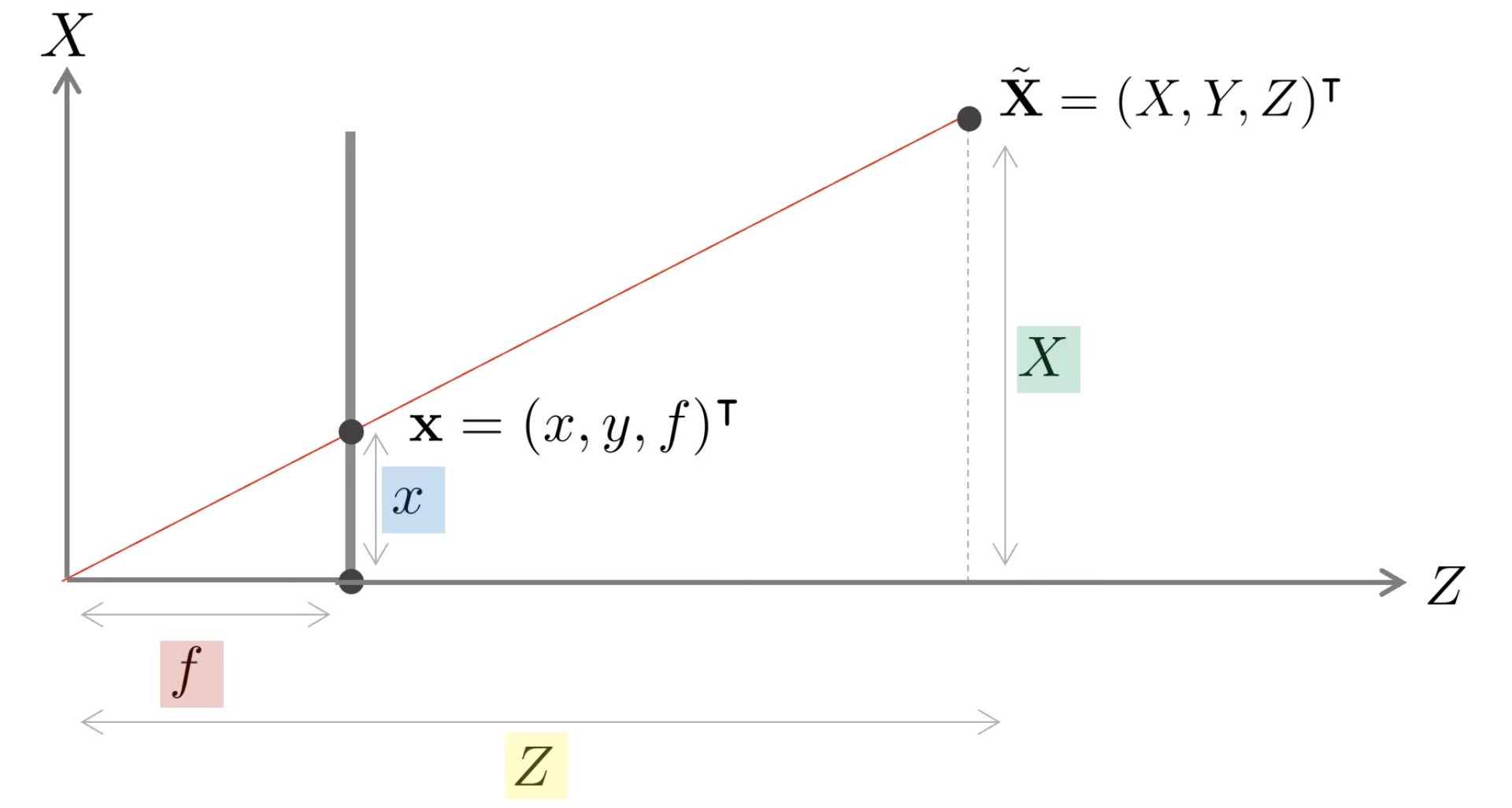
2차원 점 x = ( x , y , f ) T x=(x,y,f)^{T} x = ( x , y , f ) T
f : x = Z : X x Z = f X x = f X Z \begin{aligned} f:x &= Z:X \\ xZ &= fX \\ x &= \frac{fX}{Z} \end{aligned} f : x x Z x = Z : X = f X = Z f X X = ( X , Y , Z , 1 ) T ∈ P 3 → x = ( f X Z , F Y Z , f ) T X=(X,Y,Z,1)^{T}\in\mathbb{P}^3 \rightarrow x=(\frac{fX}{Z},\frac{FY}{Z},f)^{T} X = ( X , Y , Z , 1 ) T ∈ P 3 → x = ( Z f X , Z F Y , f ) T projection matrix P
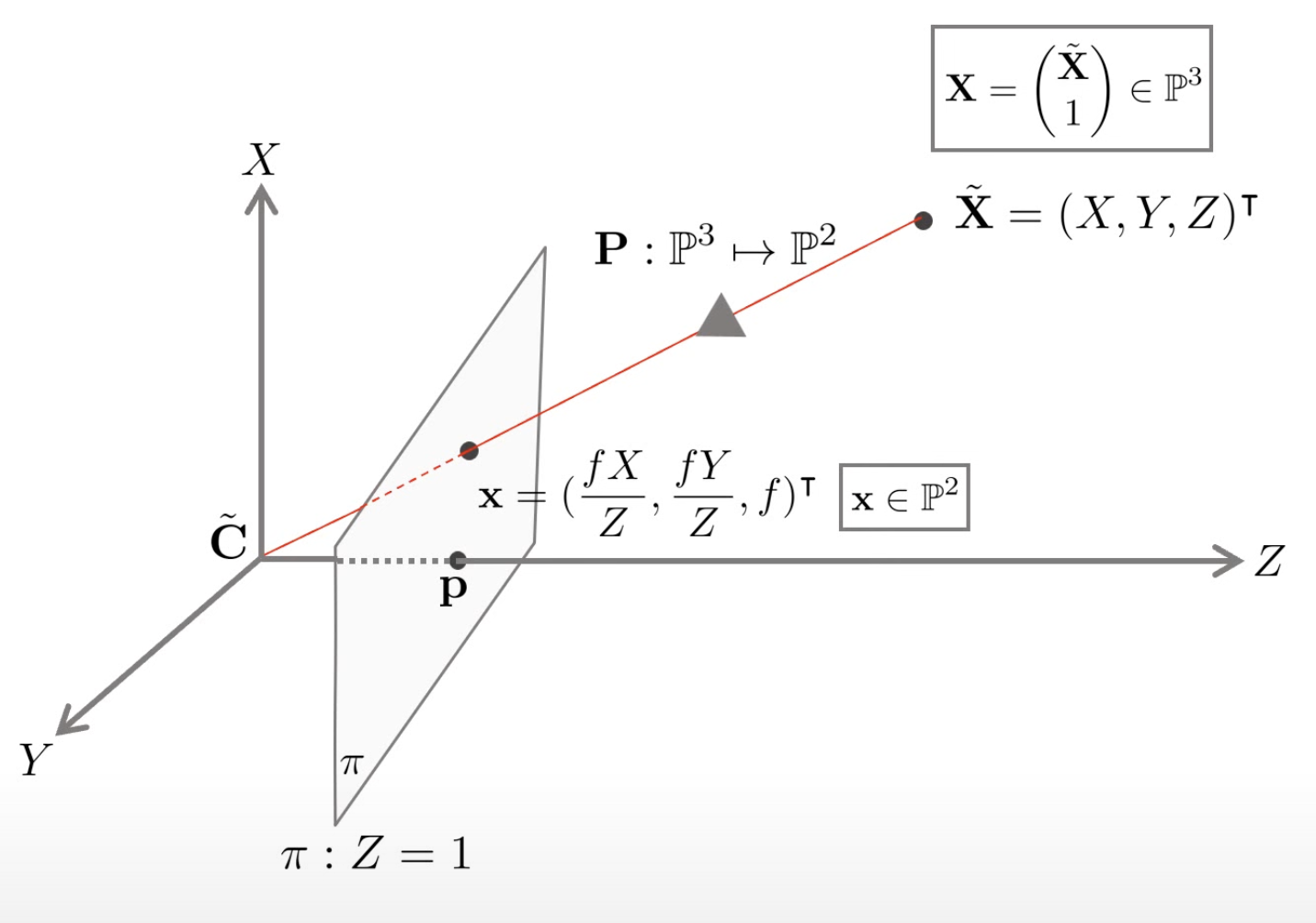
프로젝션 행렬 P는 P 3 \mathbb{P}^3 P 3 P 2 \mathbb{P}^2 P 2 x x x
P : [ X Y Z 1 ] ↦ [ f X f Y Z ] = [ f 0 f 0 f 0 ] [ X Y Z 1 ] P: \begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}\mapsto \begin{bmatrix}fX\\fY\\Z\end{bmatrix}= \begin{bmatrix}f&&&0\\&f&&0\\&&f&0\end{bmatrix} \begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} P : ⎣ ⎢ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎥ ⎤ ↦ ⎣ ⎢ ⎡ f X f Y Z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ f f f 0 0 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎥ ⎤ 위 행렬은 3차원 공간상의 한 점을 2차원 평면에 mapping하는 함수라고 볼 수 있다.
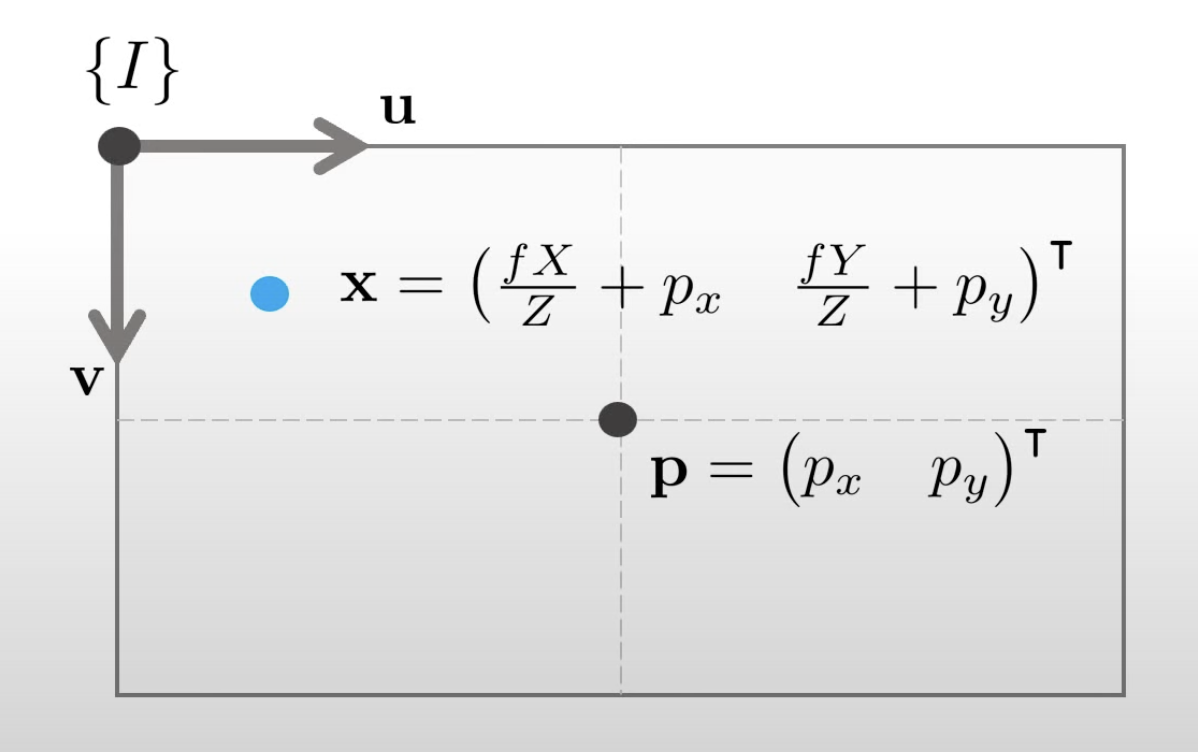
P : [ X Y Z 1 ] ↦ [ f X + Z p x f Y + Z p y Z ] = [ f p x 0 f p y 0 f 0 ] [ X Y Z 1 ] P: \begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}\mapsto \begin{bmatrix}fX+Zp_x\\fY+Zp_y\\Z\end{bmatrix}= \begin{bmatrix}f&&p_x&0\\&f&p_y&0\\&&f&0\end{bmatrix} \begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} P : ⎣ ⎢ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎥ ⎤ ↦ ⎣ ⎢ ⎡ f X + Z p x f Y + Z p y Z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ f f p x p y f 0 0 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎥ ⎤ 이 사상 함수를 내부 파라미터 행렬(intrinsic matrix) [ K ∣ 0 ] \begin{bmatrix}K|0\end{bmatrix} [ K ∣ 0 ]
Camera rotations and translation
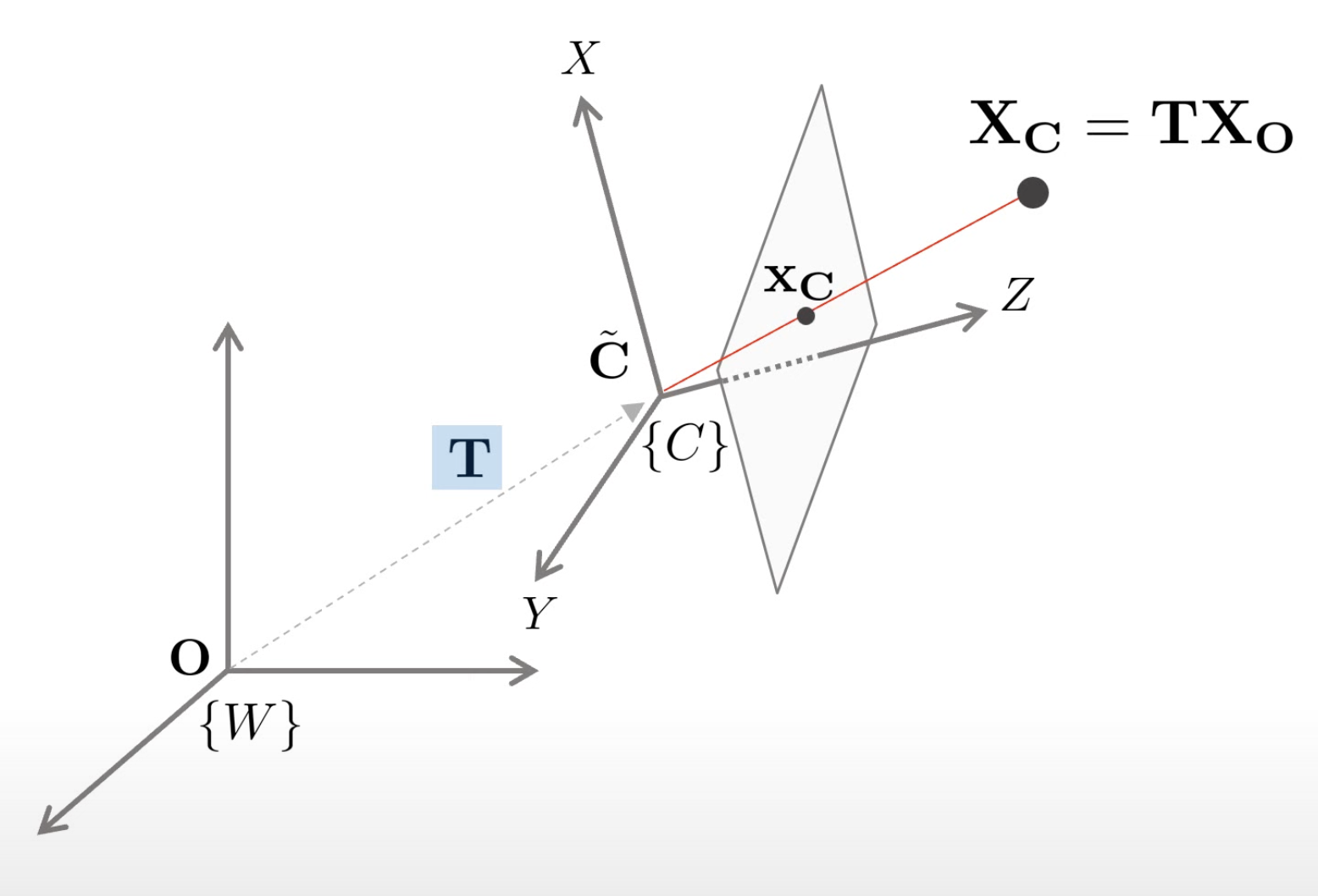
일반적으로 카메라 좌표계(C C C W W W
T = [ r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 0 0 0 1 ] T=\begin{bmatrix} r_{11}&r_{12}&r_{13}&t_1\\ r_{21}&r_{22}&r_{23}&t_2\\ r_{31}&r_{32}&r_{33}&t_3\\ 0&0&0&1 \end{bmatrix} T = ⎣ ⎢ ⎢ ⎢ ⎡ r 1 1 r 2 1 r 3 1 0 r 1 2 r 2 2 r 3 2 0 r 1 3 r 2 3 r 3 3 0 t 1 t 2 t 3 1 ⎦ ⎥ ⎥ ⎥ ⎤ X C = P X c = [ K ∣ 0 ] T X o = [ K ∣ 0 ] [ R ∣ t ] X o ∴ P = K [ R ∣ t ] ∈ R 3 × 4 \begin{aligned} X_C=PX_c&=\begin{bmatrix}K|0\end{bmatrix}TX_o \\ &=\begin{bmatrix}K|0\end{bmatrix}\begin{bmatrix}R|t\end{bmatrix}X_o \\ \therefore P&=K\begin{bmatrix}R|t\end{bmatrix} \in \mathbb{R}^{3\times4} \end{aligned} X C = P X c ∴ P = [ K ∣ 0 ] T X o = [ K ∣ 0 ] [ R ∣ t ] X o = K [ R ∣ t ] ∈ R 3 × 4 Perspective n points(PnP, P6P DLT) algorithm
3차원과 2차원 상의 대응쌍 ( X i , X w ) (X_i, X_w) ( X i , X w ) P P P
X I = P X W X I = [ u v s ] T X W = [ x y z 1 ] T \begin{aligned} X_I&=PX_W \\ X_I&=\begin{bmatrix} u&v&s\end{bmatrix}^T \\ X_W &=\begin{bmatrix} x&y&z&1\end{bmatrix}^T \\ \end{aligned} X I X I X W = P X W = [ u v s ] T = [ x y z 1 ] T Projection matrix를 월드 좌표계를 기준으로 한 3차원 공간상의 한 점을 이미지 평면상의 한 점으로 사상시키는 함수로 봤을 때, 위와 같은 식으로 나타낼 수 있다.
X I × P X W = [ s p r o w 2 T X w − v p r o w 3 T X w u p r o w 3 T X w − s p r o w 1 T X w v p r o w 1 T X w − u p r o w 2 T X w ] = 0 \begin{aligned} X_I\times PX_W & = \begin{bmatrix} sp^T_{row2}X_w - vp^T_{row3}X_w \\ up^T_{row3}X_w - sp^T_{row1}X_w \\ vp^T_{row1}X_w - up^T_{row2}X_w \end{bmatrix} \end{aligned}=0 X I × P X W = ⎣ ⎢ ⎡ s p r o w 2 T X w − v p r o w 3 T X w u p r o w 3 T X w − s p r o w 1 T X w v p r o w 1 T X w − u p r o w 2 T X w ⎦ ⎥ ⎤ = 0 X i X_i X i P X w PX_w P X w
[ 0 s X W − v X W − s X W 0 − u X W ] ⏟ A ∈ R 2 n × 12 [ P r o w 1 T P r o w 2 T P r o w 3 T ] ⏟ P ∈ R 12 = 0 \underbrace{\begin{bmatrix} 0&sX_W&-vX_W\\ -sX_W&0&-uX_W\\ \end{bmatrix}}_{A\in\mathbb{R}^{2n\times 12}} \underbrace{\begin{bmatrix} P^T_{row1} \\ P^T_{row2}\\ P^T_{row3}\\ \end{bmatrix}}_{P\in\mathbb{R}^{12}} =0 A ∈ R 2 n × 1 2 [ 0 − s X W s X W 0 − v X W − u X W ] P ∈ R 1 2 ⎣ ⎢ ⎡ P r o w 1 T P r o w 2 T P r o w 3 T ⎦ ⎥ ⎤ = 0
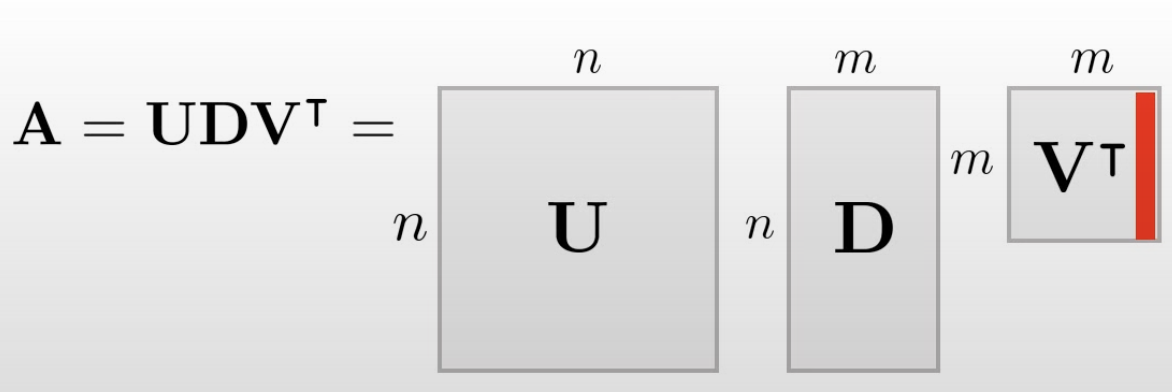
일반적인 상황에서는 데이터가 노이즈를 포함하고 있기 때문에 A는 항상 full rank이며 null sapce가 존재하지 않는다. 따라서 SVD 분해를 통해 행렬 분해를 수행한 후 V T V^T V T
하지만, 해당 알고리즘은 부정확성으로 인해 사용되지 않으며, Reprojection error를 이용한 최적화 방법에 초기값을 찾는 방법으로 응용된다.
Distortion model
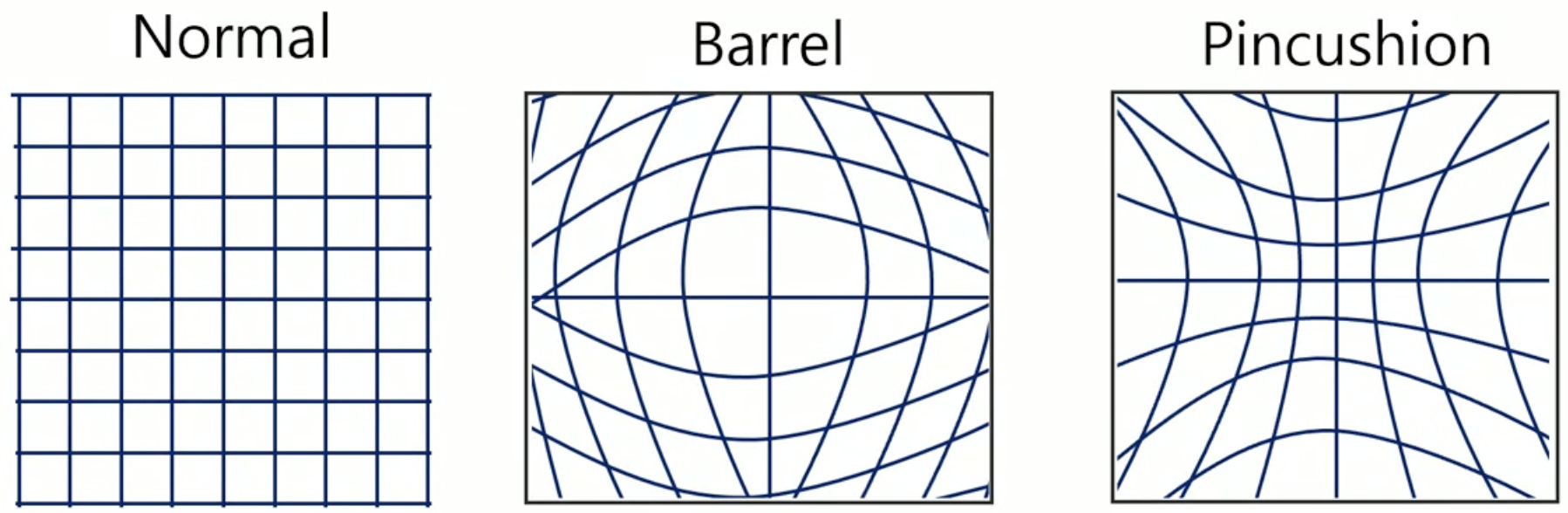
Redial distortion
카메라 자체의 왜곡을 의미한다.
x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) r = x 2 + y 2 x_{distorted} = x(1+k_1r^2+k_2r^4+k_3r^6) \\ y_{distorted} = y(1+k_1r^2+k_2r^4+k_3r^6) \\ r=\sqrt{x^2+y^2} x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) r = x 2 + y 2 Tangential distortion
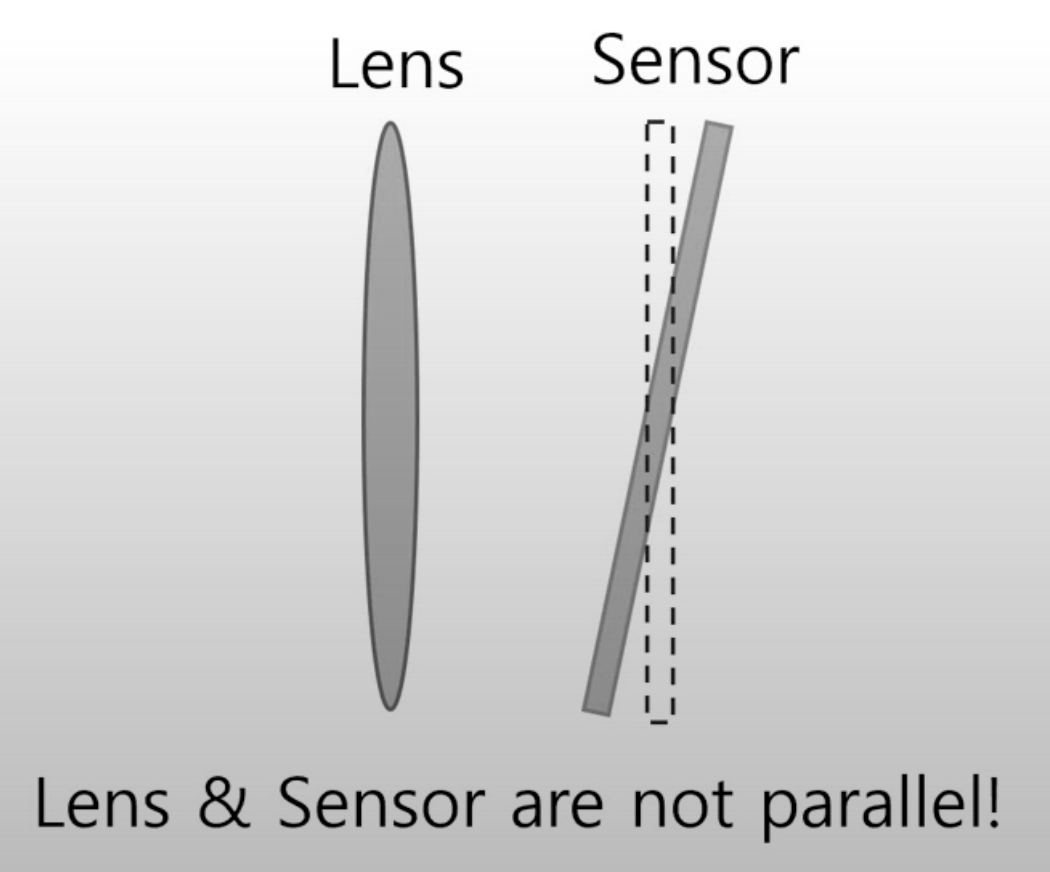
렌즈와 센서의 물리적인 차이에 의해서 나타나는 왜곡을 의미한다.
x d i s t o r t e d = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y x_{distorted} = x + 2p_1xy + p_2(r^2 +2x^2) \\ y_{distorted} = y + p_1(r^2 + 2y^2) +2p_2xy x d i s t o r t e d = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y 위 두 식은 아래와 같이 하나의 식으로 합칠 수 있다.
x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y x_{distorted} = x(1+k_1r^2+k_2r^4+k_3r^6) + 2p_1xy + p_2(r^2 +2x^2) \\ y_{distorted} = y(1+k_1r^2+k_2r^4+k_3r^6) + p_1(r^2 + 2y^2) +2p_2xy x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y 일반적으로 k 1 , k 2 , k 3 , p 1 , p 2 k_1,k_2,k_3,p_1,p_2 k 1 , k 2 , k 3 , p 1 , p 2
Zhang's method (Checkboard cailbration, ICCV 1999)
가장 보편적으로 사용되는 Camera calibration 방법으로 위 그림과 같이 체크 모양이 그려진 이미지를 통해 행렬 P를 구한다.
월드 좌표계를 체커보드의 코너점으로 설정함으로써 Z = 0 Z=0 Z = 0 X w = ( X , Y , 0 ) T X_w=(X,Y,0)^T X w = ( X , Y , 0 ) T Z Z Z
X I = P X w [ u v 1 ] = K [ r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 0 0 0 1 ] [ X Y 0 1 ] \begin{aligned} X_I &=PX_w \\ \begin{bmatrix} u&v&1 \end{bmatrix}&= K \begin{bmatrix} r_{11}&r_{12}&r_{13}&t_1\\ r_{21}&r_{22}&r_{23}&t_2\\ r_{31}&r_{32}&r_{33}&t_3\\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} X\\Y\\0\\1\end{bmatrix} \end{aligned} X I [ u v 1 ] = P X w = K ⎣ ⎢ ⎢ ⎢ ⎡ r 1 1 r 2 1 r 3 1 0 r 1 2 r 2 2 r 3 2 0 r 1 3 r 2 3 r 3 3 0 t 1 t 2 t 3 1 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ X Y 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ 회전 행렬의 경우 세번째 열을 최적화에서 제외할 수 있기 때문에 최적화할 파라미터를 줄일 수 있다. 따라서
K [ r c o l 1 , r c o l 2 , t ] ∈ R 3 × 3 K[r_{col1}, r_{col2},t] \in \mathbb{R}^{3\times3} K [ r c o l 1 , r c o l 2 , t ] ∈ R 3 × 3 3 × 3 3\times3 3 × 3
체커보드는 패턴의 길이와 개수를 모두 알 수 있으며, 동시에 이미지 상에 코너와 같은 특징을 통해 점을 추출할 수 있다. 이 두 데이터 쌍을 통해 calibration을 하는 것이다.
[ h c o l 1 h c o l 2 h c o l 3 ] ⏟ k n o w = K ⏟ u n k n o w [ r c o l 1 r c o l 2 t ] ⏟ u n k n o w n \underbrace{ \begin{bmatrix} h_{col1}&h_{col2}&h_{col3} \end{bmatrix}}_{know}=\underbrace{K}_{unknow} \underbrace{ \begin{bmatrix} r_{col1}&r_{col2}&t \end{bmatrix}}_{unknown} k n o w [ h c o l 1 h c o l 2 h c o l 3 ] = u n k n o w K u n k n o w n [ r c o l 1 r c o l 2 t ] 체크보드와 이미지 평면위에 점들의 homography 변환으로 봤을 때, 위와 같은 변환 행렬을 정의할 수 있다.
회전행렬은 열벡터 간의 직교하기 때문에 직교하는 벡터의 내적은 0인 특성을 이용하여 해결한다.