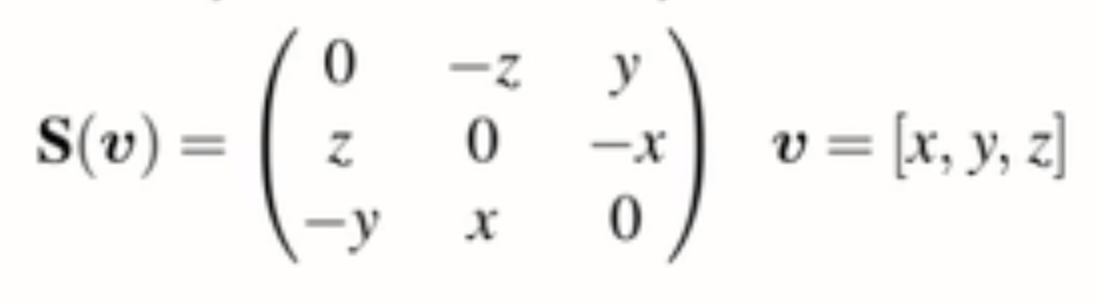3차원 공간을 이해하기 위해서 왜 2개 이상의 이미지가 필요한가?
카메라는 3차원 공간의 한 점을 카메라 좌표계로 그리고 이것을 다시 이미지 좌표계로 바꾼 것이다. 이때 변환은 행렬의 곱으로 수행되며, 역함수를 구해 이미지 좌표를 3차원 공간의 한 점으로 바꾸는 것이 가능할 거사로 생각할 수 있다. 하지만 실제로는 불가능하다.
실제로는 Extrinsic 정보는 알 수 없다. Extrinsic 정보를 알 고 있다는 것 자체가 이미 3차원 공간의 한 점의 위치를 정확하게 알 고 있다는 것과 마찬가지기 때문이다.
SLAM 자체가 3차원 공간의 한 점을 찾는 것이기 때문에 Extrinsic을 찾는 과정이라고 볼 수 있다.
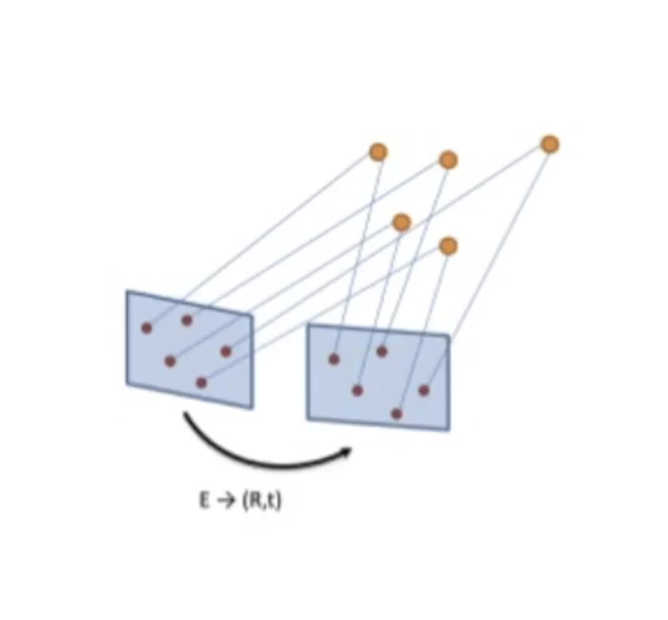
2D에서 3D로 맵핑하기 위해서는 새로운 차원의 데이터가 필요하기 때문에 최소 2장의 이미지가 필요하다. 이때 두 장면을 수집한 두 장의 이미지를 얻을 때 사용된 카메라가 이동한 위치(Rigid body motion)를 알아야 한다. Proprioceptive 센서를 통해서 카메라의 이동 정보를 얻을 수 있지만, VSLAM의 경우 이러한 센서 없이 영상의 기하학적 정보를 통해 유추할 수 있어야 한다.
이를 위해서는 두 이미지 사이의 기하학적 상관 관계에 대해서 알아야 한다.
Correspondence란?
두 영상에서 표현된 feature descripter들 간에 일치하는 정보를 의미한다.
Epipolar(2-view) geometry
동일한 3D 지점을 바라보도 있는 2개의 이미지가 있는 경우 2-view geometry라고 한다. stero camera의 경우 두 장면이 동시에 들어오지만, monocular camera의 경우 두 장면이 서로 다른 시간에 들어온다.
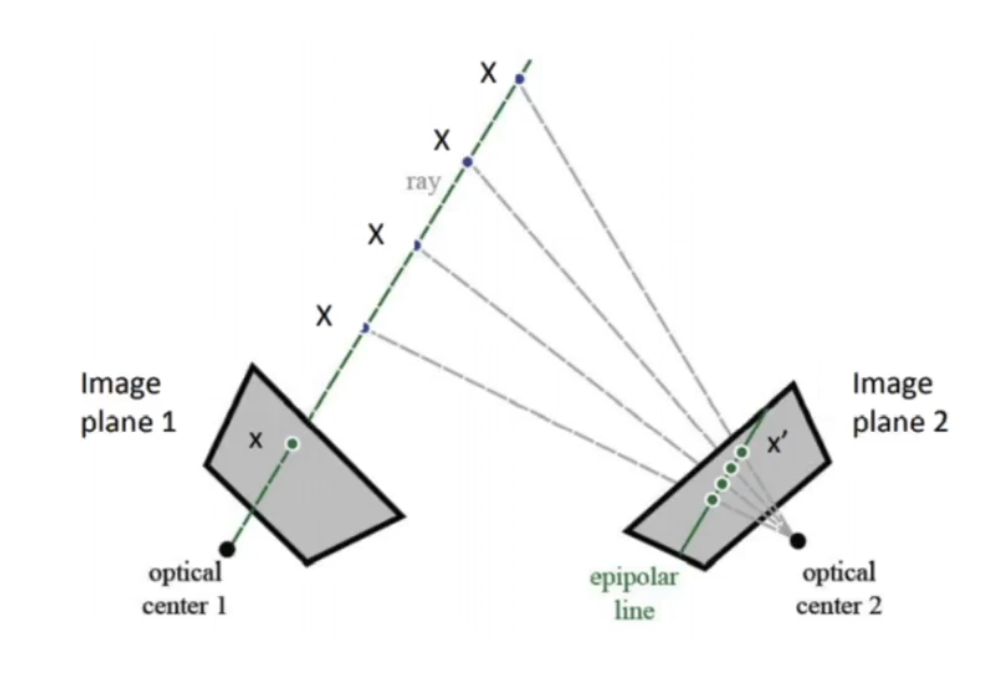
Epipolar line:
재투영(Reprojection)은 한 이미지에서 보이는 ray(빛의 이동)가 동일한 대상이 다른 이미지에 보이는 것을 의미한다. 이는 2차원으로 표현된 한 점을 3차원으로 표현하고 이를 다른 시점의 이미지 상에 2차원으로 투영시킨 것이기 때문이다.
Epipolar line은 재투영된 영상에서 나타나는 직선을 의미한다. 이때 ray 위에 존재하는 객체는 무조건 epipolar line 위에 나타난다.
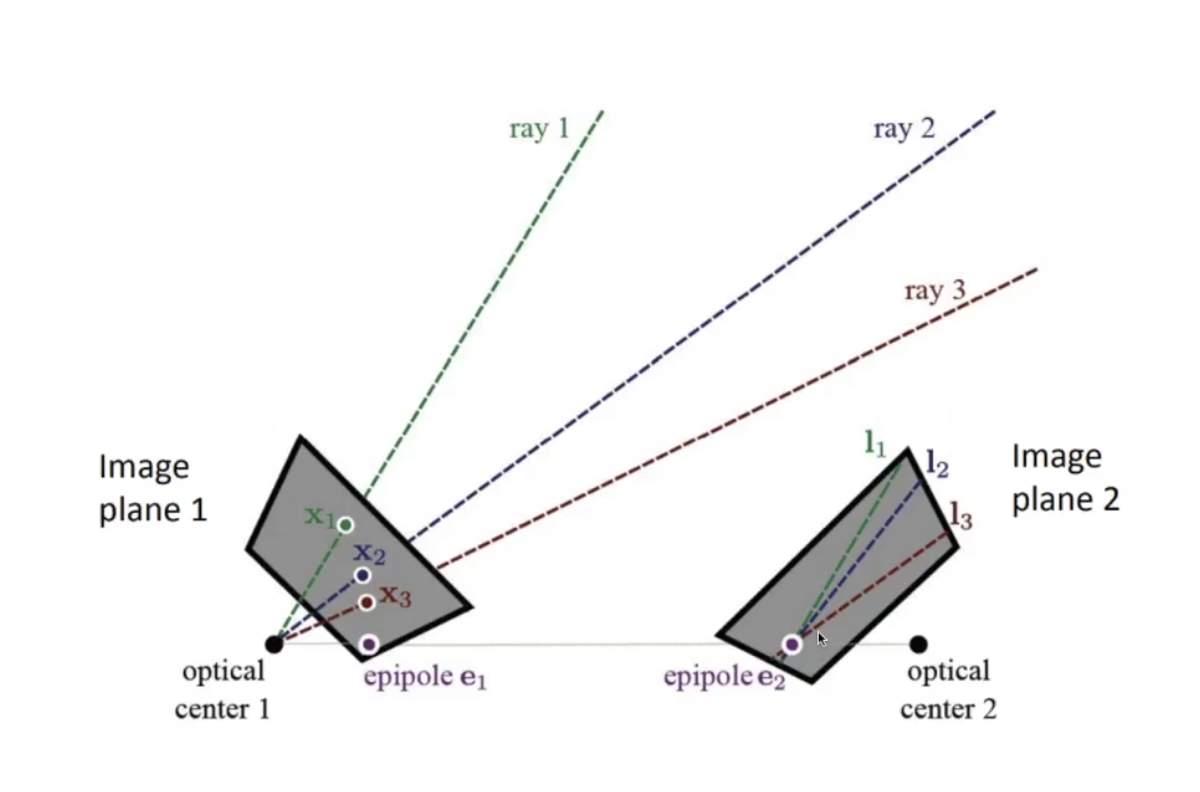
Epipole:
epipole은 ray들이 겹치는 부분이다. 잘 생각해보면 ray들은 왼쪽 카메라의 optical center에 모이게 된다. 정리하면, 왼쪽 카메라가 있었던 자리가 오르쪽 카메라에 보이는 경우에 epipole이 나타난다고 할 수 있다. 또한 왼쪽 카메라의 epipole이 보인다는 것은 왼쪽 카메라 역시 오른쪽 카메라의 epipole이 보일 확률이 높다.
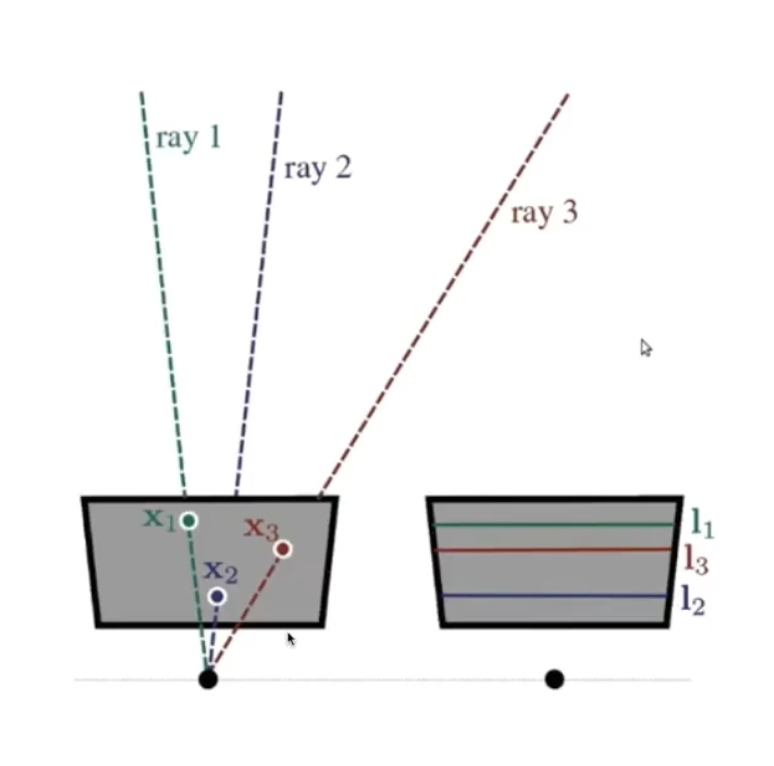
두 카메라가 서로 같은 방향을 바라보고 있는 형태의 stereo camera를 사용하는 경우 위와 같은 상황이 많이 발생한다. 이 경우에는 서로 다른 카메라가 보이지 않기 때문에 epipole이 나타나지 않다. 또한 epipolar line이 평행한 직선으로 나타난다.
평행한 선은 유클리드 공간의 무한에 거리에서 교차하지만, 유클리드 공간에서는 무한과 교차는 동시에 존재하지 않기 때문에 epipole이 생성되지 않는다.
하지만 위와 같은 상황에서 x1에 대한 대응점을 l1에서 찾을 수 있고, x2는 l2, 그리고 x3는 l3에서 찾을 수 있다. 또한 가로로 나타나기 때문에 연산이 용이하다.

위 그림은 하나의 카메라를 이용해서 VSLAM을 하는 경우에 나타나는 형태이다.epipole이 상호 이미지에서 보이지는 않지만, epipolar line이 epipole을 중심으로 방사(radial)하는 형태로 나타나는 것이 특징이다.
2D 정보에서는 앞과 뒤에 대한 정보가 없기 때문에 방사 형태로 epipolar line이 나타난다.
특히, 이런 경우에는 상대적인(relative) 움직임을 쉽게 구할 수 있다. 왜냐하면 회전 없이 단순히 직진과 같은 형태로 구할 수 있기 떄문이다.
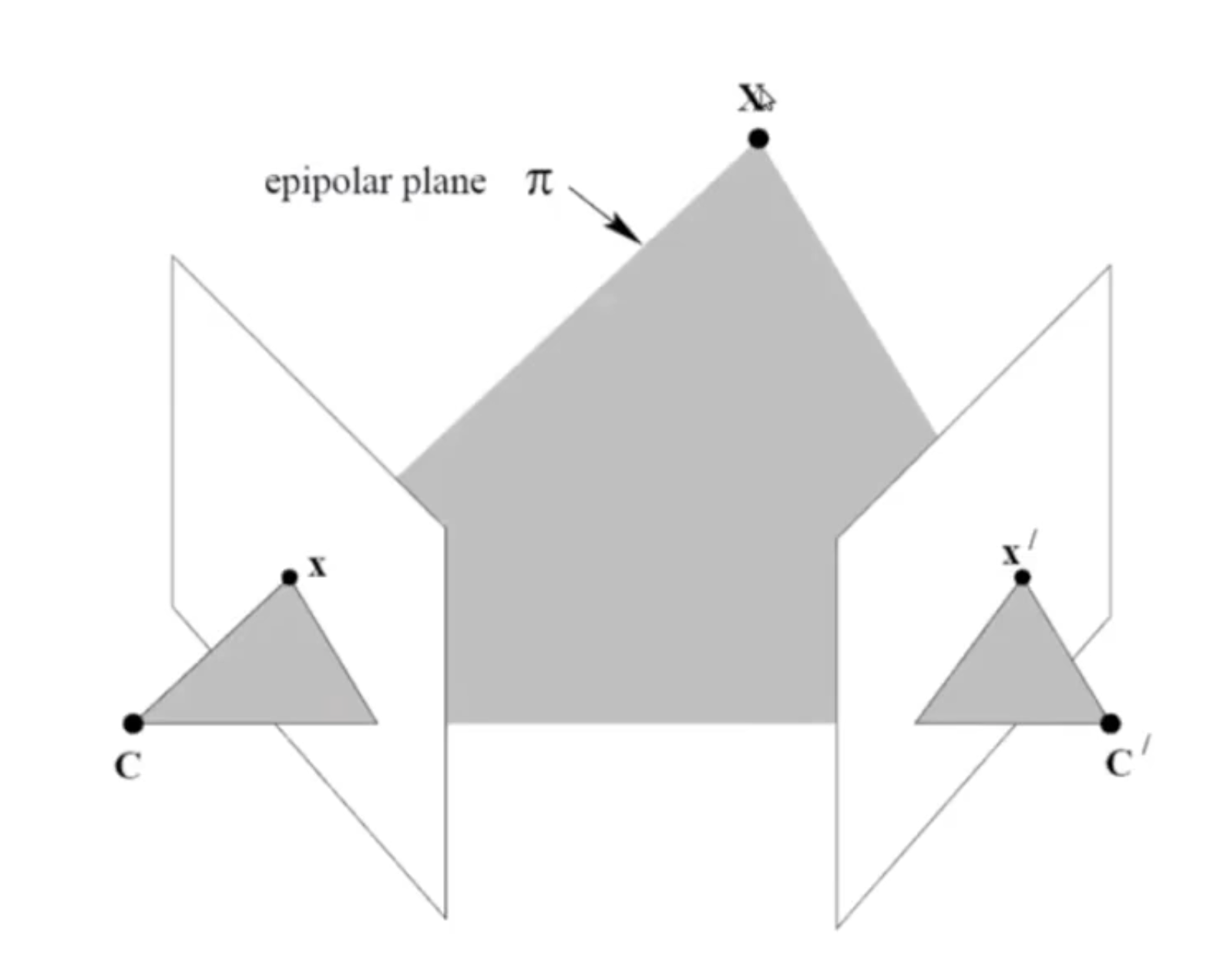
두 영상의 optical center와, 3d 상의 한 점까지 연결하면 삼각형 하나가 형성된다. 이를 epipolar plane라고 한다. epipolar plane은 epipolar line, epipole에 대한 정보를 한번에 포함하고 있어 매우 중요한 개념이다.
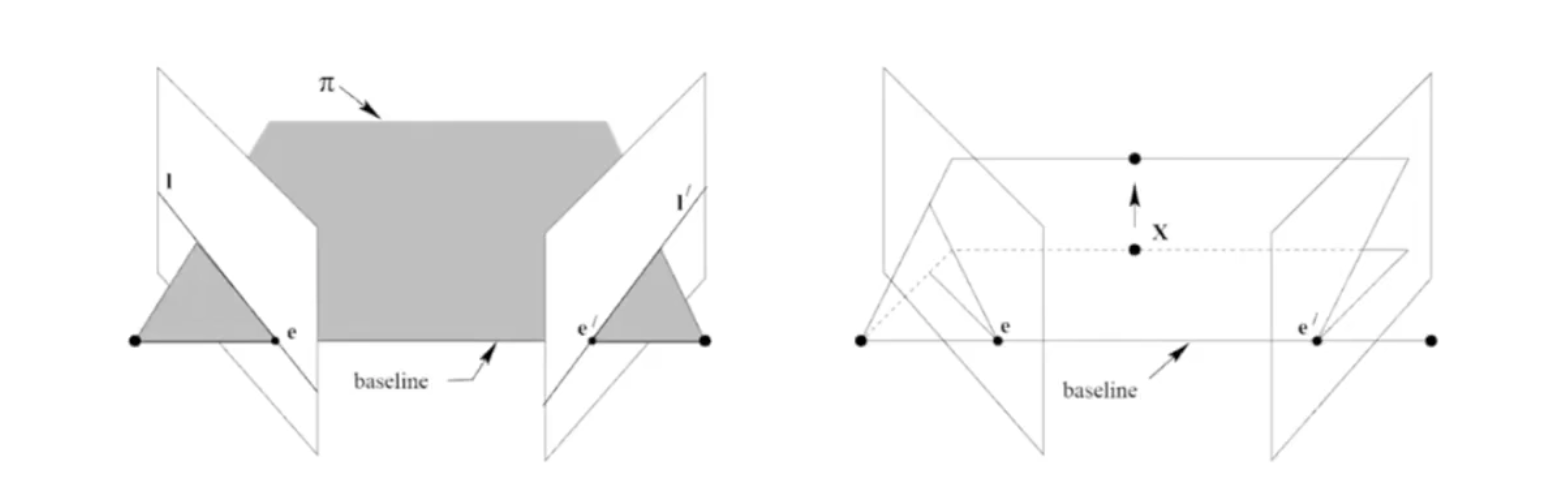
baseline은 두 영상의 optical center를 연결하는 직선을 의미한다. 두 카메라의 거리를 의미한다. baseline이 클수록 삼각 측량의 정확도가 올라간다.
이때 만약 한 점으로부터 수직으로 여러개의 3D 점을 구한다면, epipole을 기준으로 회전하는 형태로 나타난다. 이렇게 여러개의 epipolar plane이 존재할 수 있는데 이를 epipolar pencil이라고 한다.
Geometric constraint
위 요소들을 정리하면 3d point는 epipolar plane 위에 있어야하며 baseline과 접해야한다. 또한 모든 epipolar line들은 epipole과 교차해야 한다.
2d point, epipole, 3d point가 한 평면 위에 있어야 하며, 이를 co planar라고 한다.
두 이미지 사이의 관계를 표현하는 방법
Essential matrix
카메라 간의 모션을 추정하기 위해 두 영상에 나타나는 포인트 간의 correspondence를 정확하게 아는 것이 중요하다. epipolar constraint는 서로 다른 영상에 대한 correspondence를 만드는데 중요한 역할을 한다. 또한 essention matrix을 통해 카메라의 motion을 설명할 수 있다.
다시 말해, Essential matrix, E는 서로 다른 영상에 포인트들을 연결해주는 역할을 한다. 왼쪽 영상과 오른쪽 영상에 보이는 상을 엮어주는 방법으로 기학적인 제약을 만든다고 할 수 있다.
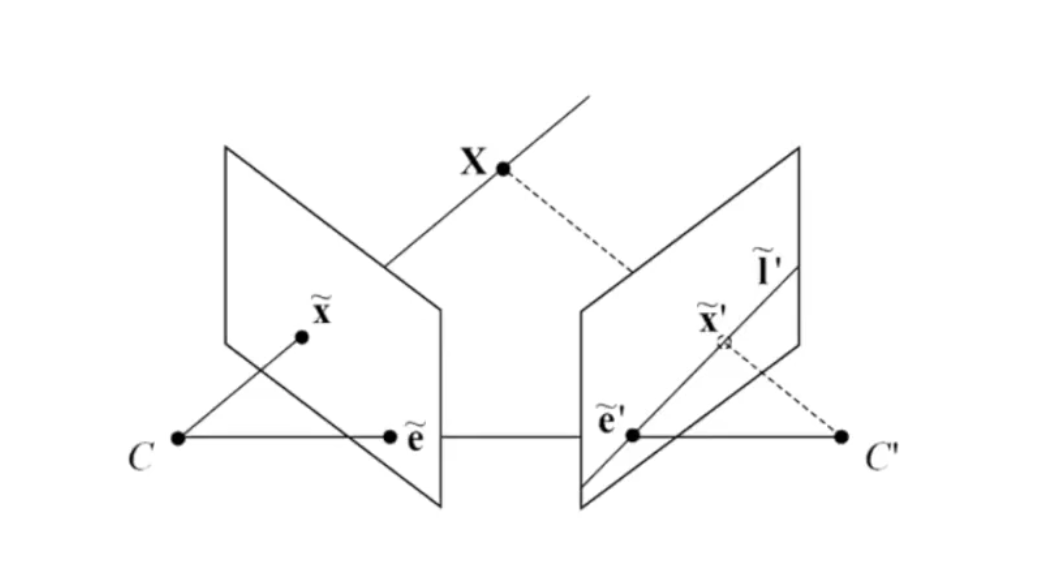
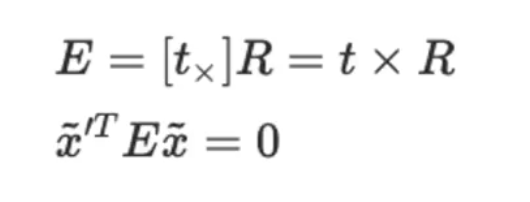
에서 E는 두 영상에 나타나는 포인트의 correspondence를 엮어주는 역할을 수행하기 때문에 이를 위해 두 카메라 간의 회전과 이동에 대한 내용을 담고 있을 것이다.
Essential matrix(E)는 translation과 rotaion(SO(3))의 cross product로 만들어진다. 이떄, 벡터 형태인 t는 Skew symmetric matrix로 변환하여 3x3 형태의 행렬로 만들어 개산된다. 이렇게 구한 E는 SVD를 통해 이동 행렬(t)와 회전 행렬(R)로 분해한다.
Fundamental matrix
3차원 공간의 의 경우 실수 형태로 나타난다. 반면에 이미지 상의 는 픽셀로 표현되기 때문에 이를 설명할 수 있는 intrinsic K행렬의 정보가 필요하다.
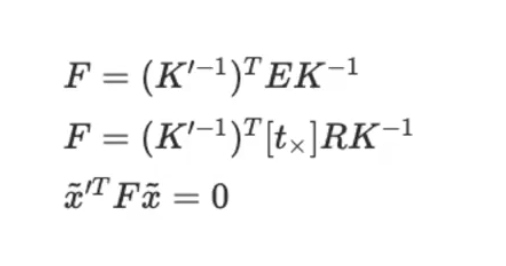
위 식에서 볼 수 있듯이 왼쪽 카메라와 오른쪽 카메라에 대한 intrinsic 정보를 곱해주어 epipolar contraint에 추가해주는 것을 확인할 수 있다.
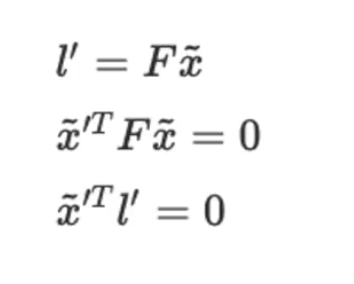
Fundamental matrix, 에 를 곱하면 다른 영상의 eipolar line의 식이 나온다. 또한 이 line과 해당 영상의 한 점 은 0이 된다(이 부분은 왜 그런지 찾아볼 것). 이 성질을 이용하여 이미지 픽셀과 을 dot product해서 0이 되는 픽셀들을 이용하면 epipolar line위에 존재하는 점들을 알아낼 수 있다.
5-point algorithm
최소 5개의 픽셀에 대한 correspondence가 존재하는 경우에 사용할 수 있는 알고리즘이다. Essention matrix를 구하는 경우에 주로 사용된다. Essention matrix는 Rotation에 관한 내용인 6개의 변수로 구성되며, scale 값을 제외한 5 DoF(Degree of Freedom)을 갖는다.
8-point algorithm
최소 8개의 픽셀에 대한 correspondence가 존재하는 경우에 사용할 수 있는 알고리즘이다. Fundamental matrix를 구하는 경우에 주로 사용된다. translation에 관한 내용인 Rotation에 관한 내용인 마지막으로 intrinsic에 대한 내용인 총 8개의 변수를 갖지만 Essention matrix와 마찬가지로 scale 값은 구할 수 없기 때문에 이를 제외한 7개의 DoF(Degree of Freedom)을 갖는다.
DoF는 데이터를 추론하기 위해 필요한 최소한의 데이터의 개수를 의미힌다. 최소한의 데이터로 데이터를 추론하는 알고리즘을 Minimal solver라고 한다. Essention matrix의 경우 5개 정보로 추론이 가능하기 때문에 여기에 해당하며, 반대로 Fundamental matrix의 경우 7개보다 많은 8개의 데이터로 추론이 가능하기 때문에 여기에 해당하지 않는다.
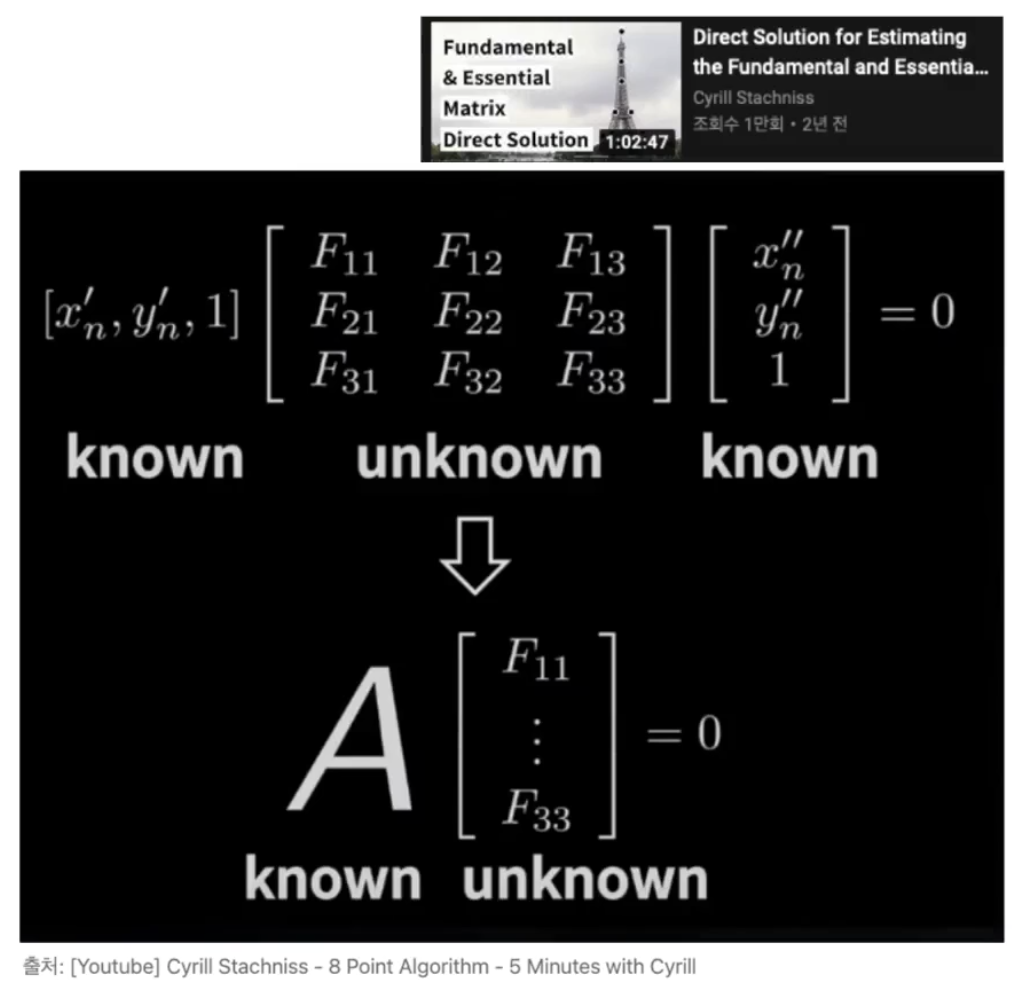
opencv 구현체
recoverPose() essention matrix를 계산할 수 있는 함수가 OpenCV에 구현되어 있다.
https://docs.opencv.org/3.4/d9/d0c/group__calib3d.html#gadb7d2dfcc184c1d2f496d8639f4371c0
findFundamentalMat() fundamental matrix를 계산할 수 있는 함수가 OpenCV에 구현되어 있다.
https://docs.opencv.org/3.4/d9/d0c/group__calib3d.html#ga59b0d57f46f8677fb5904294a23d404a