
2d point를 통해 3d point를 Mapping에 사용되는 가장 기본적인 기술이다.
General triangulation
monocular camera나 대부분에 환경에서 3d point를 추정하는 방법이다.
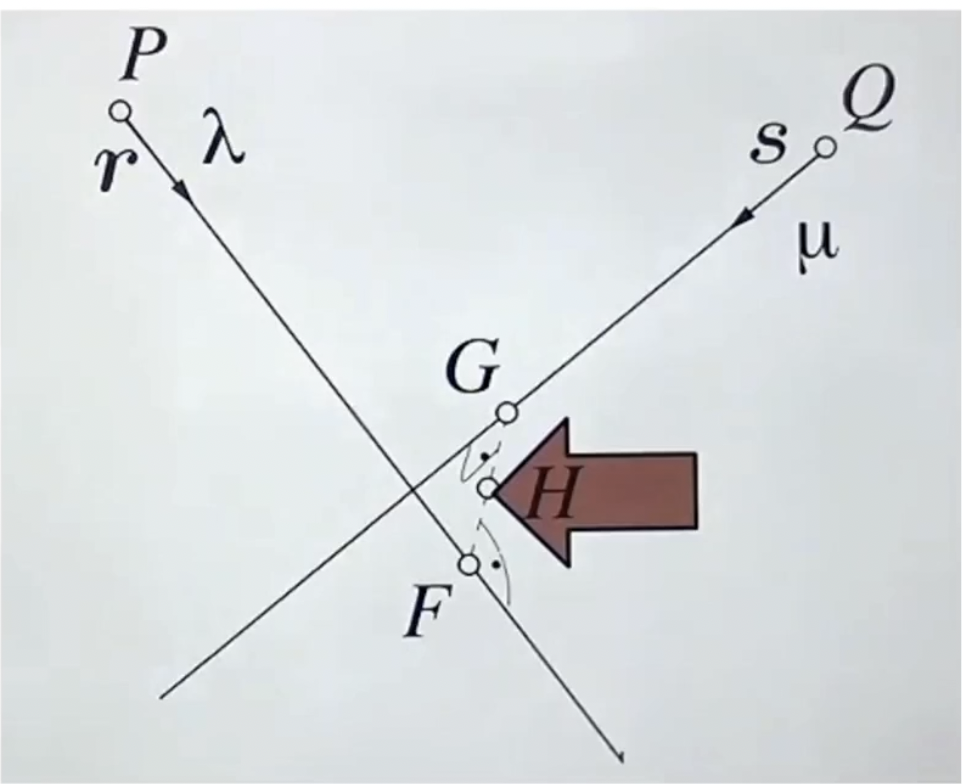
위 그림은 두 카메라의 중점 P와 Q로 부터 나오는 ray가 한 점에서 모이는 것을 시각화한 그림이다. 하지만 현실에서는 카메라의 노이즈를 비롯한 다양한 이유로 정확하게 한 점에서 만나는 경우는 없다. 때문에 두 카메라의 노이즈가 어느정도 유사하다는 것을 전제로 H에서 만난다고 가정한다.
이때, 두 ray(p와 q)는
f=p+λrg=q+μs
로 정의할 수 있다. λ는 scale이고 r은 방향을 나타내는 단위 벡터이다. 알고있는 정보는 ray의 시작 위치(카메라의 위치) p와 q이다. 이를 통해 방향 벡터와 scale을 구할 수 있다.
r=R′TkX′s=R′′TkX′′
kX′(왼쪽 카메라)와 kX′′(오른쪽카메라)는 camera의 calibration이 된 각 카메라의 픽셀 위치를 의미한다. 거기에 world frame에서 camera frame으로 옮기는 rotation matrix R을 곱한 형태이다. 다만 여기서는 RT 즉, R의 역행렬을 곱하기 때문에 camera frame에서 world frame으로 변환한다고 생각할 수 있다. 따라서 r과 s는 world frame에서의 3d ray의 형태가 된다고 볼 수 있다.
kX′=(x′,y′,c)TkX′′=(x′′,y′′,c)T
x, y는 픽셀, c는 focal length이다.
다시 위 그림을 통해 H의 기하학적 특징을 살펴보자. 먼저, H는 r과 s 사이의 가장 가까운 지점이 되어야한다. 때문에 vector f-g는 r과 s에 대해서 수직이어야 한다. 서로 수직인 벡터의 내적은 0이되는 성질을 이용해서 다음의 식을 얻을 수 있다.
(f−g)⋅r=0(f−g)⋅s=0(p+λr−q−μs)⋅r=0(p+λr−q−μs)⋅s=0
위 식은 식2개로 2개의 미지수 λ와 μ를 알아낼 수 있다. p와 q를 실제 카메라의 위치로 바꾼 다음 식을 다시 정리하면 다음과 같다.
(XO′+λr−XO′′−μs)Tr=0(XO′+λr−XO′′−μs)Ts=0(XO′−XO′′)Tr+λrTr−μsTr=0(XO′−XO′′)Ts+λrTs−μsTs=0[rTrrTs−sTr−sTs][λμ]=[(XO′−XO′′)T(XO′−XO′′)T][rs]
위 식처럼 Ax=b의 형태로 정리가 가능하다. 두 개의 미지수(x)에 대한 두 개의 식으로 표현되기 때문에 역행렬이나, 행렬 분해를 통해서 해를 구할 수 있다.
H=2F+G
두 벡터의 중간을 선택하는 방법으로 구할 수 있다. 다만 이는 두 카메라에 대한 신뢰도가 50%로 가정한 상태이기 때문에 두 지점의 중간을 선택한 것이다. 일부 다른 알고리즘에서는 불확실성을 기준으로 신뢰도를 조절하는 방법도 있다.
Stereo triangulation
두 영상으로부터 얻은 featrue diparity를 이용해서 3d point를 추정하는 방법이다.
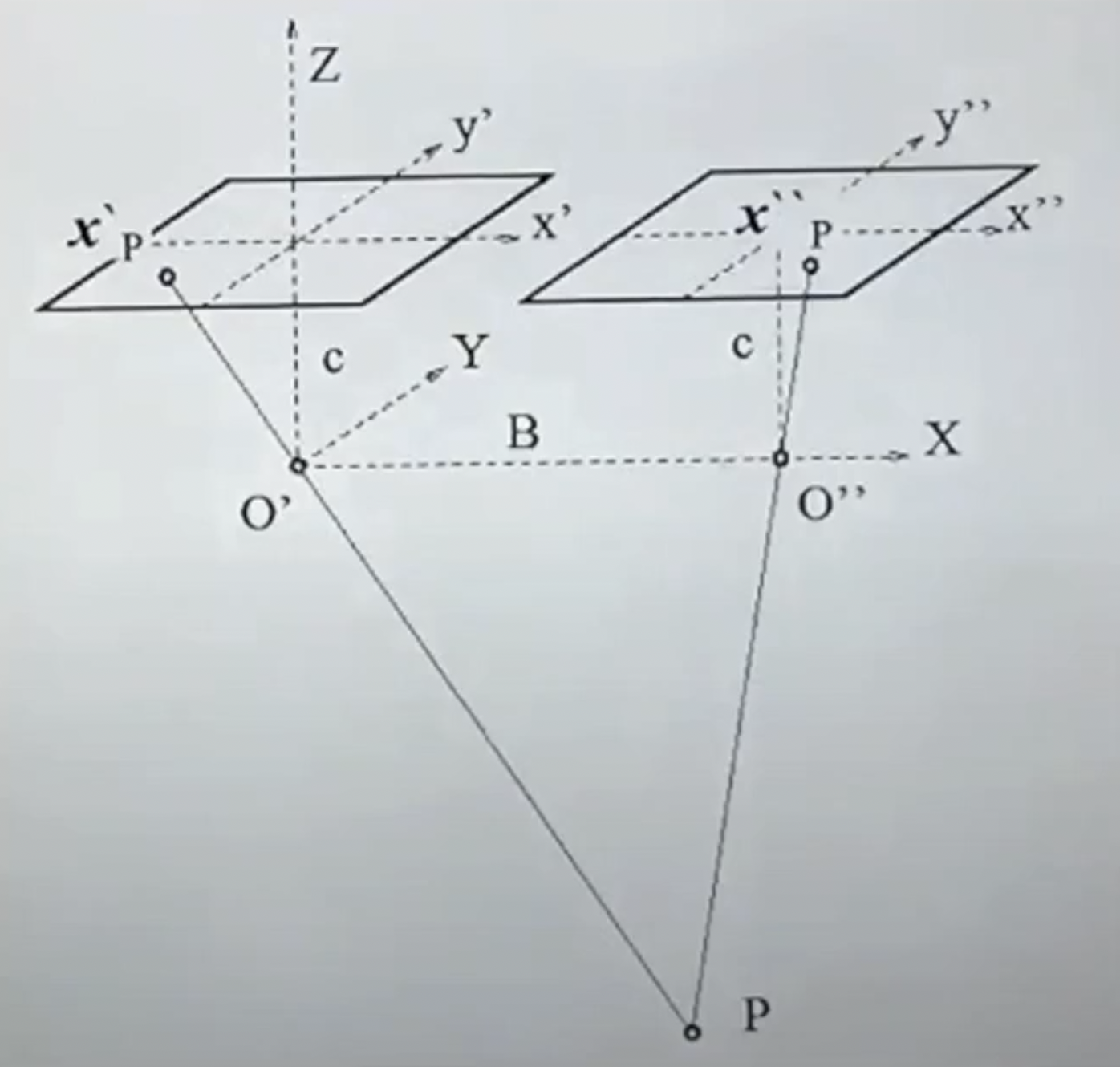
위 그림은 두 카메라가 전방을 향하고 있고, 같은 plane에 놓여있는 상황이다. 또한 baseline을 알고 있고, 각각에 이미지에 나타나는 featrue 인 x′, x′′위치를 알고 있고 두 feature의 차이를 알고 있는 상황을 가정한다. 두 feature의 차이가 disparity 또는 parallax라고 한다.
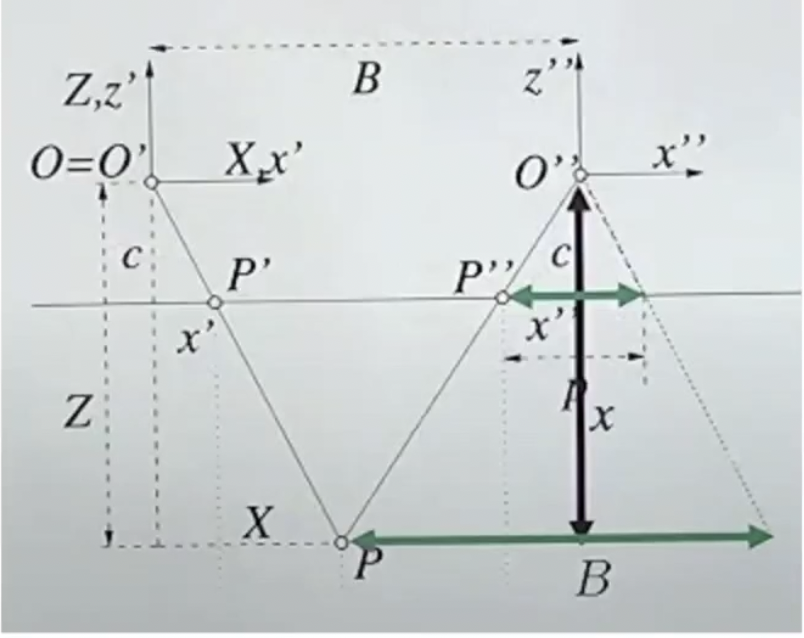
위 그림은 첫 번째 그림을 top-view에서 도식화해서 나타낸 그림이다. O는 camera의 center이며, B는 baseline, P는 3d world의 한 점이 된다. 왼쪽에 있는 카메라의 ray를 오른쪽 카메라에서 나온 것 처럼 옮겨주면, 초록색 화살표 처럼 나타나개 된다. 이때 우리가 알고싶은 정보인 Z는 삼각형의 닮음을 통해 구할 수 있다.
cZ=x′−x′′BZ=c−(x′′−x′)B
위 식에서 B와 c는 상수이다. 즉, 두 장면의 시차(parallex)를 안다면 depth(Z)를 알 수 있다는 것을 알 수 있다.
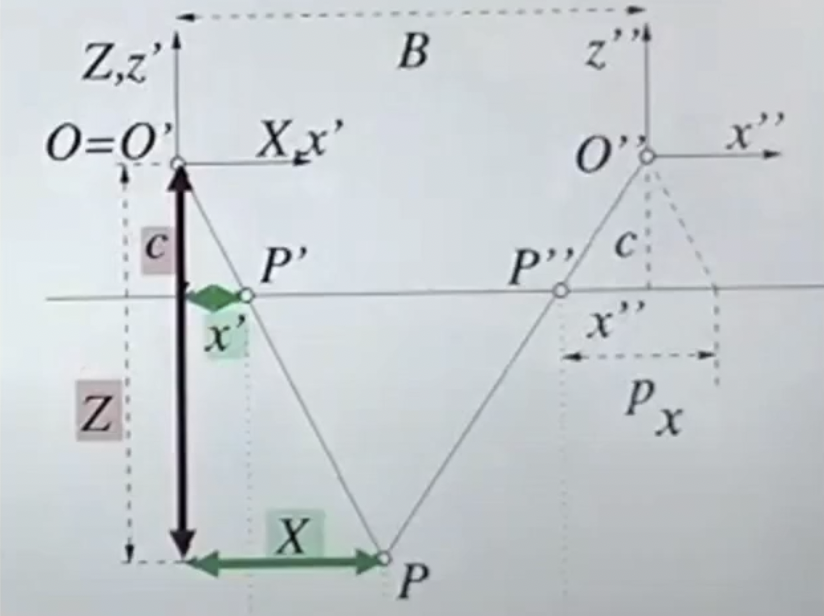
같은 원리로 X의 위치도 구할 수 있다.
c:x′cZX=Z:X=x′X=x′−(x′′−x′)B
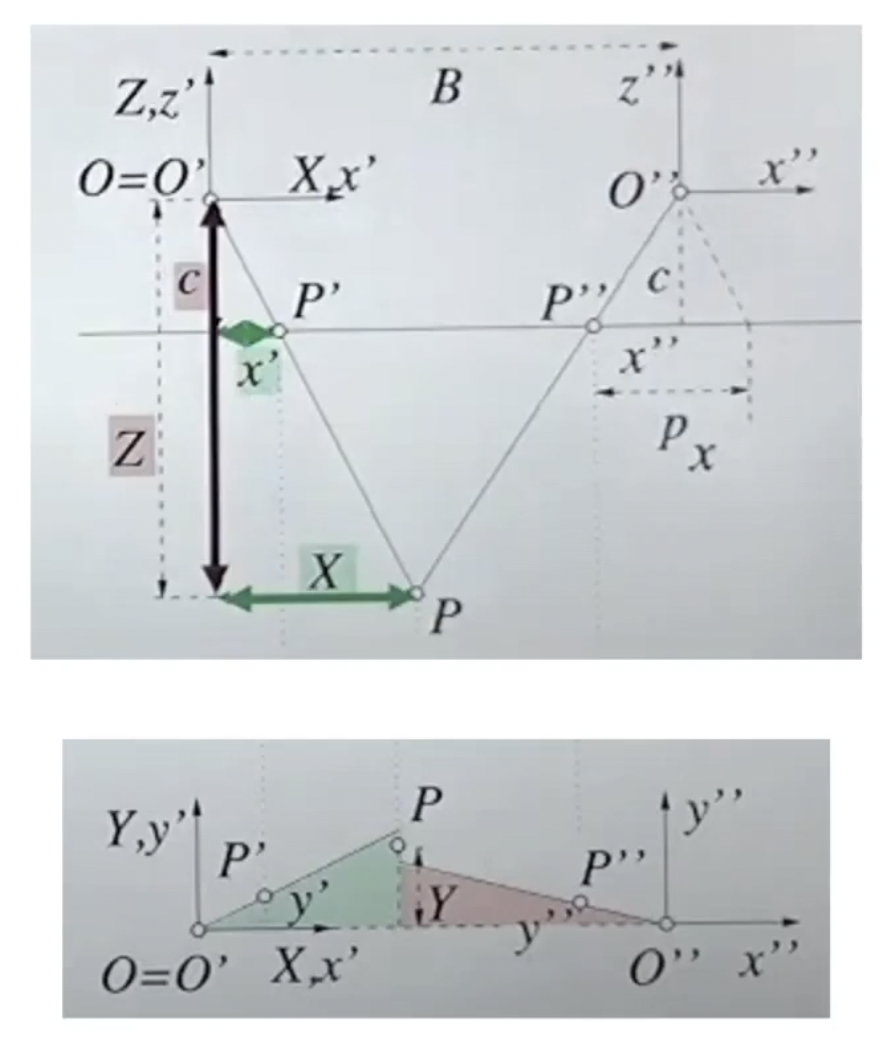
Y 또한 같은 원리로 구할 수 있다. 다만 3차원 공간에서 두 카메라에서 나온 ray 정확하게 일치하는 것은 어렵기 때문에 평균을 이용해서 구한다.
X:YX:YXYYYY=x′:y′=x′:2y′+y′′=x′2y′+y′′=Xx′2y′+y′′=x′−(x′′−x′)Bx′2y′+y′′=−(x′′−x′)B2y′+y′′
위 식을 통해 3차원 공간의 한 점인 P의 Y좌표까지 알 수 있다.








훌륭한 글이네요. 감사합니다.