[Cryptography(암호학)] 7주차-Digital Signatures

본 포스팅은 Coursera | Cryptography - Jonathan Katz 강의를 수강하며 정리했습니다.

1-1 Digital Signatures

Cryptography 7주차 강의정리를 시작하겠습니다. 이번 주차에서는 지난 포스팅에서 잠깐 다룬 digital signatures(전자서명)에 대해 더 자세히 공부해보겠습니다.

1. Digital Signatures

Digital signatures(전자서명)은 public-key 설정에서 integrity(무결성)를 제공하는 하나의 매커니즘입니다. 무결성을 제공한다는 점에서 MAC(메시지 인증 코드)과 유사하지만, 몇 가지 중요한 차이점이 있습니다. 그 전에 전자서명에 대해 간단히 살펴봅시다.

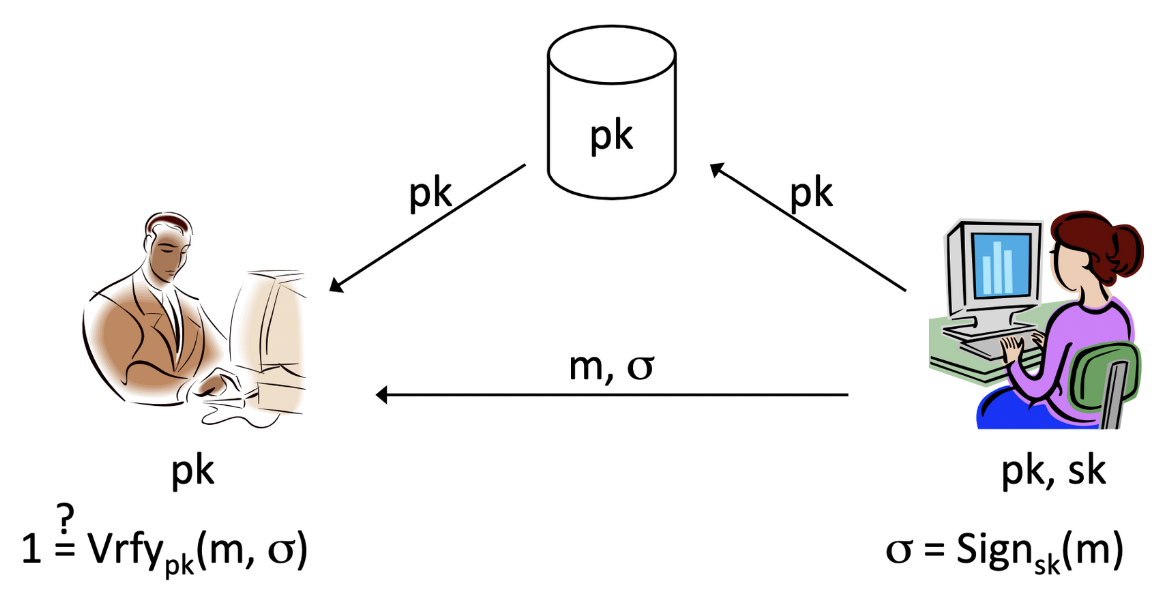
그림처럼 공개 키 $pk$를 주고 받는 두 당사자가 있습니다. Alice가 Bob에게 메시지 $m$을 전달할 때, 본인이 해당 $m$을 만들었다는 것을 증명하기 위해 $Sign_{sk}(m)=\sigma$를 함께 보냅니다. Bob은 $m$에 대해서는 주어진 $pk$로 복호화하여 $m$을 알아내고, $\sigma$에 대해서는 $Verify_{pk}(m, \sigma)$ 알고리즘을 통해 message $m$을 전달한 사람이 Alice라는 것을 검증할 수 있습니다.

2. security

위 전자서명 전달과정에서, Bob은 Alice의 $sk$는 알 수 없지만 signature $\sigma$에 대한 검증은 충분히 할 수 있습니다. 이 말인즉슨, signature $\sigma$를 보고 검증할 수 있는 그 어떤 공격자도 새로운 메시지에 대하여 유효한 새로운 서명을 위조할 수 없어야 합니다.

3. Prototypical application

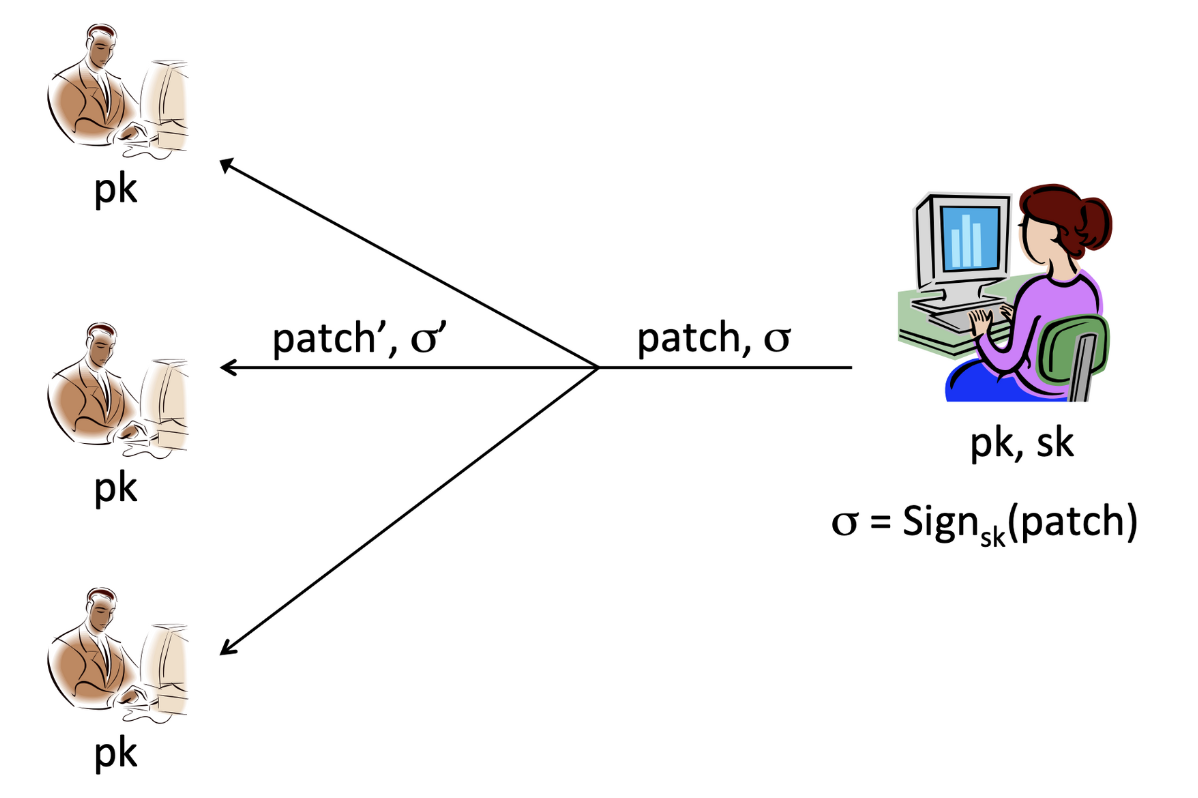
Digital signatures(전자서명) 프로토타입을 소프트웨어 프로그램에 적용해봅시다. 위 그림에서 Alice는 소프트웨어를 배포하려는 entity이고, Bob은 소프트웨어의 $pk$를 알고 있는 client입니다. Alice는 프로그램을 개선할 때마다 업데이트를 위한 패치를 유저에게 발행하는데, 중간에 패치가 공격자에 의해 위조되지 않도록 $Sign_{sk}(patch)=\sigma$와 patch를 함께 전송합니다. Bob은 전송받은 패치가 Alice로부터 온 것인지 확인합니다. 이때 공격자의 목표는 위 그림처럼 패치를 수정하여 위조된 패치를 Bob에게 보내는 것입니다.

4. Comparison to MACs?

Digital signatures(전자서명)의 방법은 MACs(메시지 인증 코드)의 운용방식과 매우 유사해보입니다. 그렇다면 둘의 차이점은 무엇일까요? Digital signatures(전자서명) 대신 MACs의 알고리즘을 이용하여 $\sigma$를 생성해보겠습니다.

| Method 1

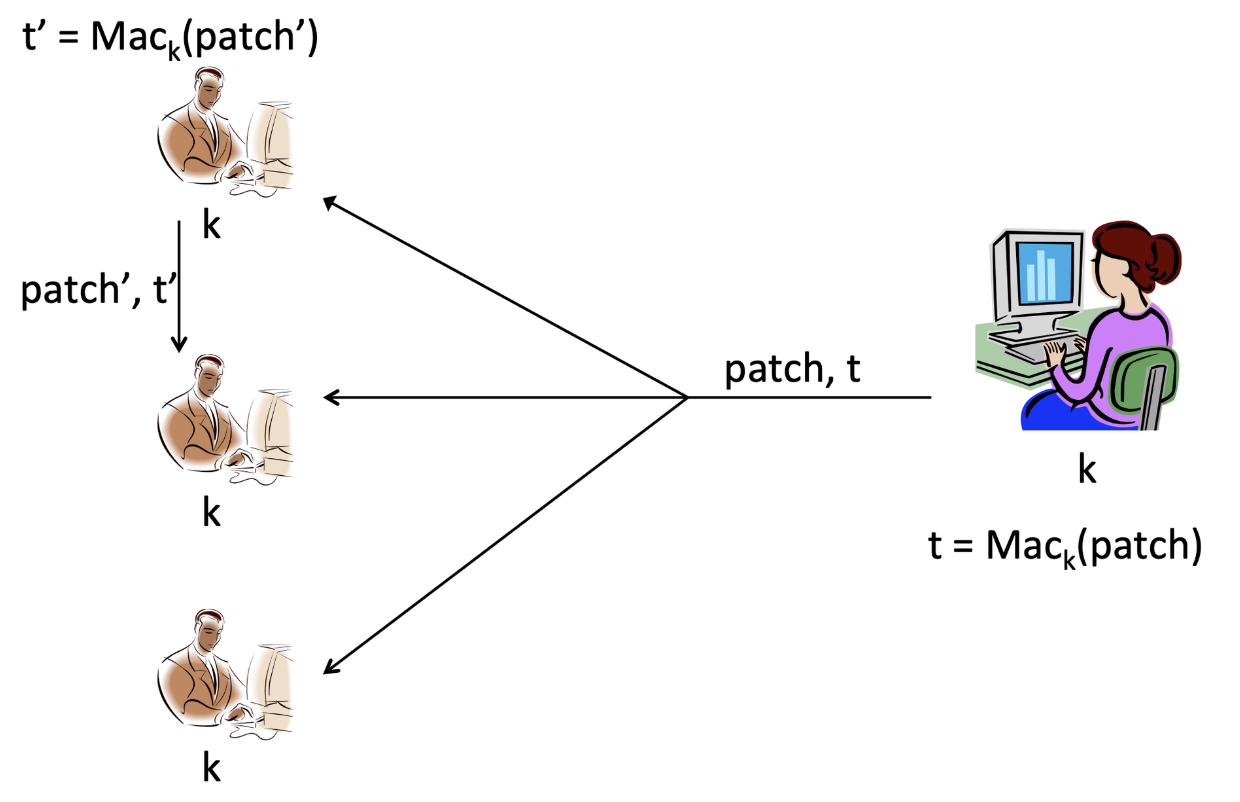
위 그림에서 발신자 Alice는 $t=MAC_k(patch)$를 이용하여 key $k$에 대한 tag를 생성하여 Bob에게 전송합니다. 이때 수신자들 Bob은 tag가 유효한지 검사할 능력이 있어야하기 때문에 발신자 Alice의 key $k$를 알고 있습니다.

위 방법은 결함이 있습니다. 위처럼 수신자 Bob은 key $k$를 알고 있기 때문에, $MAC_k(patch')$를 통해 새로운 tag를 만들어낼 수 있습니다. 만약 수신자들 중 한 명이 악의적인 목적으로 이상한 패치 $patch'$와 이에 해당하는 tag $t'$를 전송한다면, 이를 전송받은 수신자는 이상한 tag $t'$를 올바른 패치로 인식할 수 있습니다.

| Method 2

위 방법은 모든 수신자가 동일한 key $k$를 공유하고 있기 때문에 문제가 생겼습니다. 이를 해결하고자 이번엔 수신자마다 서로 다른 key들을 Alice와 공유하도록 만들어 봅시다.

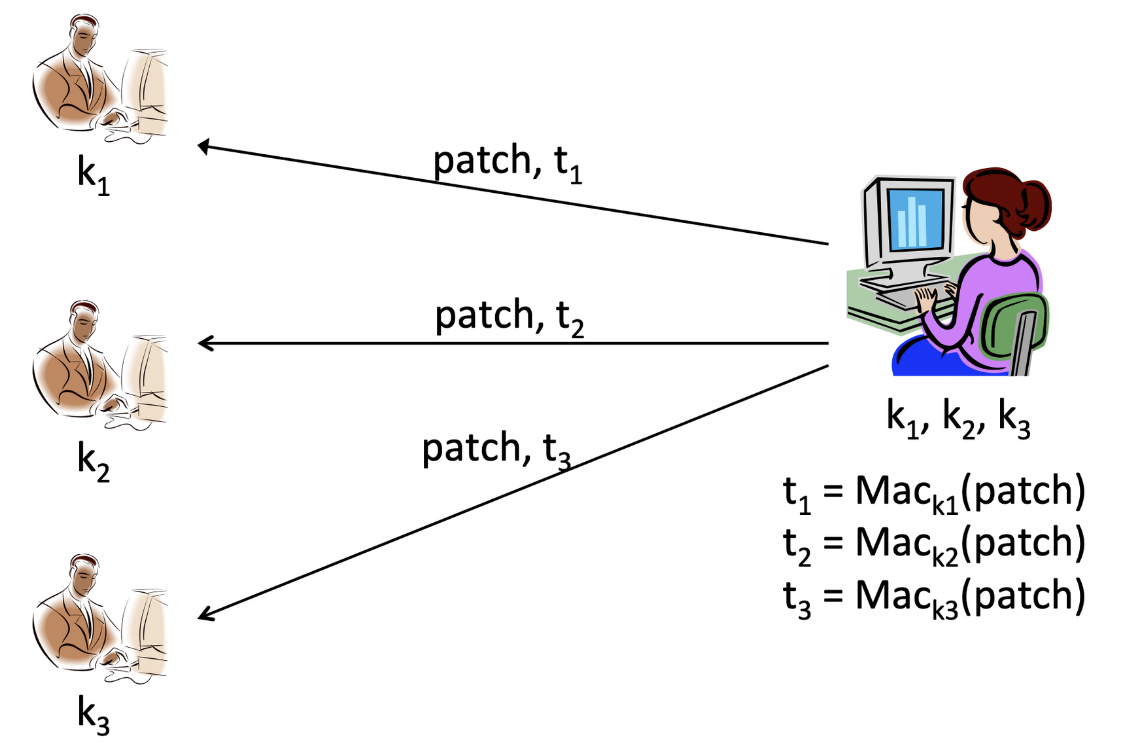
위 그림처럼 tag를 생성하여 전송하면, 수신자들 간에 악의적인 공격을 충분히 막아낼 수 있습니다. 하지만 Alice 입장에선 수신자들마다 서로 다른 key를 이용하여 tag를 만들어야하기 때문에, 수신자가 많아질수록 많은 키를 배포하고 관리해야 한다는 문제가 생깁니다.

따라서 Digital signatures(전자서명)은 아래와 같은 조건을 만족해야 합니다.

1. Public verifiability(공개검증가능성)
   : 누구나 서명을 검증(verify)할 수 있어야 한다.
2. Transferability(양도가능성)
   : 다른 사람에게 서명을 양도할 수 있다.
3. Non-repudiation(부인방지성)
   : 송신자는 수신자에게 보낸 정보를 부인할 수 없다.

MAC과 non-repuditation에 대한 성질을 비교해보면, MAC은 key에 대한 엑세스 권한이 없으면 tag의 진위여부를 확인할 수 없으므로 부인방지까지는 보장할 수 없습니다. Key는 해당 송신자만 지니고 있기 때문에, 그 key가 정확한지 검증할 방법이 없기 때문입니다.

1-2 Digital signatures 2

1. Signature schemes

Digital signatures(전자서명)의 signature scheme을 정의해봅시다. Signature scheme은 세 개의 PPT 알고리즘으로 구성되어 있습니다.

• $Gen(1^n)$ : output pk, sk (키 생성)
• $\sigma ← Sign_{sk}(m)$ : output $\sigma$ (서명 생성)
• $Vrfy_{pk}(m, \sigma)$ : output 1 or 0 (증명)

이때 모든 메시지 $m$과 $Gen$ 알고리즘을 거친 키 $pk, sk$에 대하여, 아래 식을 만족합니다.

2. Security?

| Threat model

위 signature scheme에서의 공격자는 Adaptive chosen-message attack이라는 공격모델을 사용합니다. 위 공격은 공격자가 선택한 메시지에 대한 sign을 얻을 수 있는 방식입니다.

| Security goal

공격자는 송신자에 의해 sign이 완료되지 않은 어떤 메시지에 대해서도 유효한 signature를 위조할 수 없어야 합니다. 이때 공격자는 송신자의 public key를 알고 있는 상태입니다. 이는 완전히 위조가 불가능하다는 점에서 Existential unforgeability를 만족해야 security goal에 도달한다는 말입니다.

3. Formal definition

위에서 정의한 security에 따라 scheme을 정의해봅시다.

Scheme: $\mathrm{\Pi}$ $\;\;/\;\;$ Attacker: $A$
$Forge_{A, \Pi}(n):$
$1.\;\; pk, sk \leftarrow Gen(1^n)$
$2.\;\; A$ interacts with oracle $Sign_{sk}(\cdot)$ $\;\;(M$ is the set of messages$)$
$3.\;\; A \; output \; (m,\sigma)$
$4.\;\; A \;$ succeeds, and the experiment evaluates to 1,
$\;\;\;\;\; if \; Vrfy_{pk}(m,\sigma) = 1 \; and \; m \notin M$

위 scheme에서 공격자 $A$가 유효한 signature를 만드는 결과는 $Forge_{A, \Pi}(n)$로, 1이 나오면 공격자가 성공, 0이 나오면 성공하지 못함을 나타냅니다. 한편, Signature에 대한 security는 아래와 같습니다.

4.Replay attacks

다만 위 정의로 replay attack까지 막을 수 있는 것은 아닙니다. 가령, Alice가 Bob에게 새로운 소프트웨어 패치를 보내는 과정에서 공격자가 작년에 Alice가 보냈던 패치와 서명을 그대로 보낸다면, 유효한 서명이므로 Bob 입장에서는 이를 걸러낼 방법이 없습니다.

5. Hash-and-sign paradigm

이번에 볼 서명 알고리즘은 hash와 관련되어 있습니다. MAC을 공부할 때 Hash and MAC을 공부했었는데요, 이와 동일한 방식으로 메시지에 대한 서명을 바로 만드는 것이 아니라 메시지를 해시함수에 넣은 다이제스트 H(m)을 이용해 서명을 만드는 기법입니다.

Hash-and-sign paradigm
$\Pi'=(Gen,\;Sign',\;Vrfy')$
$Sign'_{sk}(m) = Sign_{sk}(H(m))$
$Vrfy'_{pk}(m,\sigma) = Vrfy_{sk}(H(m),\sigma)$

$H : \{0,1\}^*→\{0,1\}^n$인 해시함수에 대하여 위와 같이 정의했습니다. 달라진 것은 메시지 $m$에 대하여 해시함수를 넣은 다이제스트를 서명 알고리즘에 대입하는 것입니다. 위 방식처럼 해시함수를 이용하여 서명을 만든다면, HMAC처럼 임의의 길이의 메시지에 대해서도 signature를 만들 수 있습니다. 따라서 굳이 메시지 입력의 길이를 맞출 필요가 없습니다.

그럼 위 알고리즘의 안전성을 살펴봅시다. 안전성을 증명하는 방식은 HMAC에서와 동일하게 진행됩니다.

Theorem
만약 $\Pi$가 안전하고 해시함수 $H$가 collision-resistant라면, $\Pi'$도 안전하다

| Proof

송신자가 $m_1, m_2,..., m_i$에 대하여 메시지 인증을 하려고 합니다.

이때 공격자는 위조한 $(m, \sigma)$를 만드는데, 위조하려는 message는 그 어떤 $m_i$와 같은 값이면 안됩니다. 이 때 두 가지 경우가 생깁니다.

$H(M)=H_(M_i)$ for some i

첫 번째는 공격자가 위조로 만든 해시가 $m_i$의 어떤 해시값과 같을 때입니다. 즉, collision이 일어났을 때입니다. 여기서 요점은 공격자가 해시함수의 collision을 먼저 발견했다는 것이죠. 하지만 앞서 전제에서 해시함수가 collision-resistance라고 가정했으므로, $m$과 $m_i$의 해시가 같은 쌍을 찾는 것은 불가능합니다.

$H(M)\neq h_i$ for all i

두 번째는 $m$의 해시 다이제스트가 모든 i에 대해 $h_i$와 같지 않은 경우입니다. 즉 공격자가 만들어낸 위조문이 유효하다면, 이전에 송신자로부터 받은 $h$에서 어떠한 단서를 찾았다는 것입니다. 하지만 이는 서명 알고리즘이 안전하다는 가정이 전제되었기 때문에 $h$로부터 유효한 단서를 얻는 것은 실현 불가능합니다.

2-1 RSA-based signatures

이번 강의에서는 앞서 공부한 signature scheme을 RSA를 기반으로 만들어보려고 합니다. RSA를 간단히 복습해봅시다! RSA는 factoring을 기반으로 만들어진 암호화 scheme이었습니다. 길이가 동일한 두 소수 $p$, $q$를 뽑아 두 수의 곱인 $N$을 생성합니다. 이때 $e*d=1 \bmod \phi(N)$을 만족하는 공개 키 $(N,e)$와 비밀 키 $(N,d)$를 생성하여 암호를 주고받습니다.

1. "Plain" RSA signatures

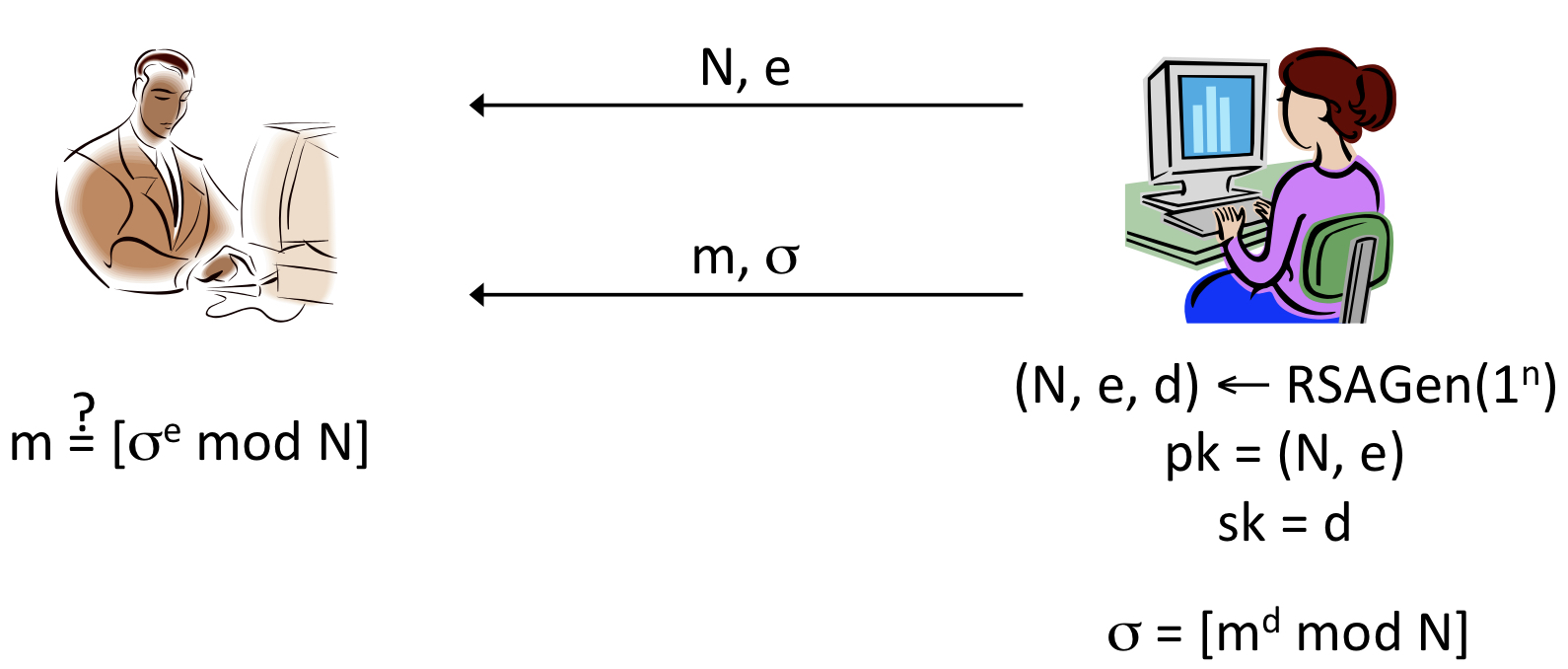
위 그림에서 두 당사자 Alice와 Bob이 있습니다. Alice는 $RSAGen(1^n)$을 통해 랜덤 속성을 지닌 $(N, e, d)$를 생성합니다. 여기서 $d$를 private-key로 세팅을 한 뒤, Bob에게 자신의 public-key인 $N$과 $e$를 전송합니다.
Alice가 Bob에게 메시지 $m$을 보낼 때, $d$로 서명 $\sigma$을 만듭니다. 이때 $\sigma=[m^d \bmod N ]$을 만족해야 합니다. 이렇게 만든 $\sigma$를 $m$과 같이 전송하면, Bob은 $[\sigma^e \bmod N]$의 결과값이 $m$이 나오는지 공개키를 통해 검증할 수 있습니다.

| Security?

위 signature scheme의 안전성은 어떨까요? 이는 RSA assumption에 의해 증명가능합니다. $N$과 $e$가 주어졌을 때 $d$를 구하는 일은 어렵고, factoring은 hard problem이기 때문에 공개키 만으로 $d$를 계산하는 것은 어렵습니다.

2. Attack

하지만 위 scheme은 특정 공격에 취약하다는 단점이 있습니다. "Plain" RSA signatures를 뚫는 공격을 살펴봅시다.

| Attack 1

첫 번째 공격은 특정 메시지에 대해 $e^{th}$ root를 계산하기 쉽다는 것입니다. 결론은 $m=1$이라면 어떤 수를 제곱하더라도 1이 나오기 때문에 그 결과값을 유추하기가 굉장히 쉬울 뿐더러 다른 key에 대하여 겹치는 결과가 생길 수도 있습니다.

| Attack 2

두 번째 공격으로, 랜덤 메시지에 대해 서명이 가능하다는 것입니다. 임의의 $\sigma$를 선택한 뒤, $m$을 $\sigma^e\,\bmod\,N$으로 세팅하면 역으로 랜덤 메시지를 수신자가 계산할 수 있습니다. Unforgeability를 만족하려면 모든 $m$에 대해 위조가 불가능해야 하는데, 이 자체가 위조가 가능한 것이므로 공격에 취약하다고 볼 수 있습니다.

| Attack 3

마지막으로, 두 개의 signature를 합쳐 제 3의 signature를 만들 수 있습니다.
$\sigma_1$, $\sigma_2$ 가 public-key $N,e$를 통해 만든 $m_1$, $m_2$ 의 signature 라고 합시다. 이때, $\sigma' = [\sigma_1 \cdot \sigma_2 \,\bmod\, N]$ 을 생성하면 이는 아래 식에 의해 $m' = [m_1 \cdot m_2 \,\bmod\, N]$ 의 signatue를 생성하는 것을 가능하게 만듭니다.

3. RSA-FDH

위와 같은 공격을 막기 위해, plain RSA signature scheme을 수정할 필요가 있었습니다. 이를 해결하고자 RSA-FDH가 등장합니다. RSA-FDH는 RSA scheme에 "cryptographic transformation"을 메시지에 적용한 것으로, 쉽게 말해 hash-and-sign 패러다임을 적용한 방식입니다. 자세한 scheme을 살펴봅시다.

• public key: (N, e)
• private key: d
• $Sign_{sk}(m) = H(m)^e \,\bmod\, N$
• $Vrfy_{pk}(m,\sigma) = output \; 1 \; iff \; \sigma^e = H(m) \,\bmod\, N$

| Intuition?

메시지에 대해 해시함수를 적용하는 순간, 공격자는 앞서 말한 attack들을 할 수 없게 됩니다. 해시는 랜덤한 값과 구분할 수 없는데, 이는 $e^{th}$ root를 구하기 힘들다는 것과 같기 때문입니다.
Signature로 생성된 값이 H($m_1$), H($m_2$)가 되므로, signature 두 개를 곱해서 만든 값은 절대 메시지를 두 개를 곱해서 만든 signature로 생성할 수 없습니다. Attack 3에서 가능했던 식이 아래와같이 불가능으로 바뀌게 됩니다.

| Security of RSA-FDH

만약 해시함수가 random function으로 매핑되어 있다면 RSA-FDH는 RSA assumption 하에 secure합니다. 실제로 RSA PKCS #1 v2.1 표준이 적용되어 사용되는데, 이를 사용하면 랜덤과 가까운 수준의 RSA-FDH를 얻을 수 있습니다.

2-2 Identification schemes

Identification scheme은 말그대로 사용자 인증 프로토콜입니다. 이번 강의에서는 identification scheme을 이용하여 signature scheme을 만들어보려고 합니다.

1. Identification schemes

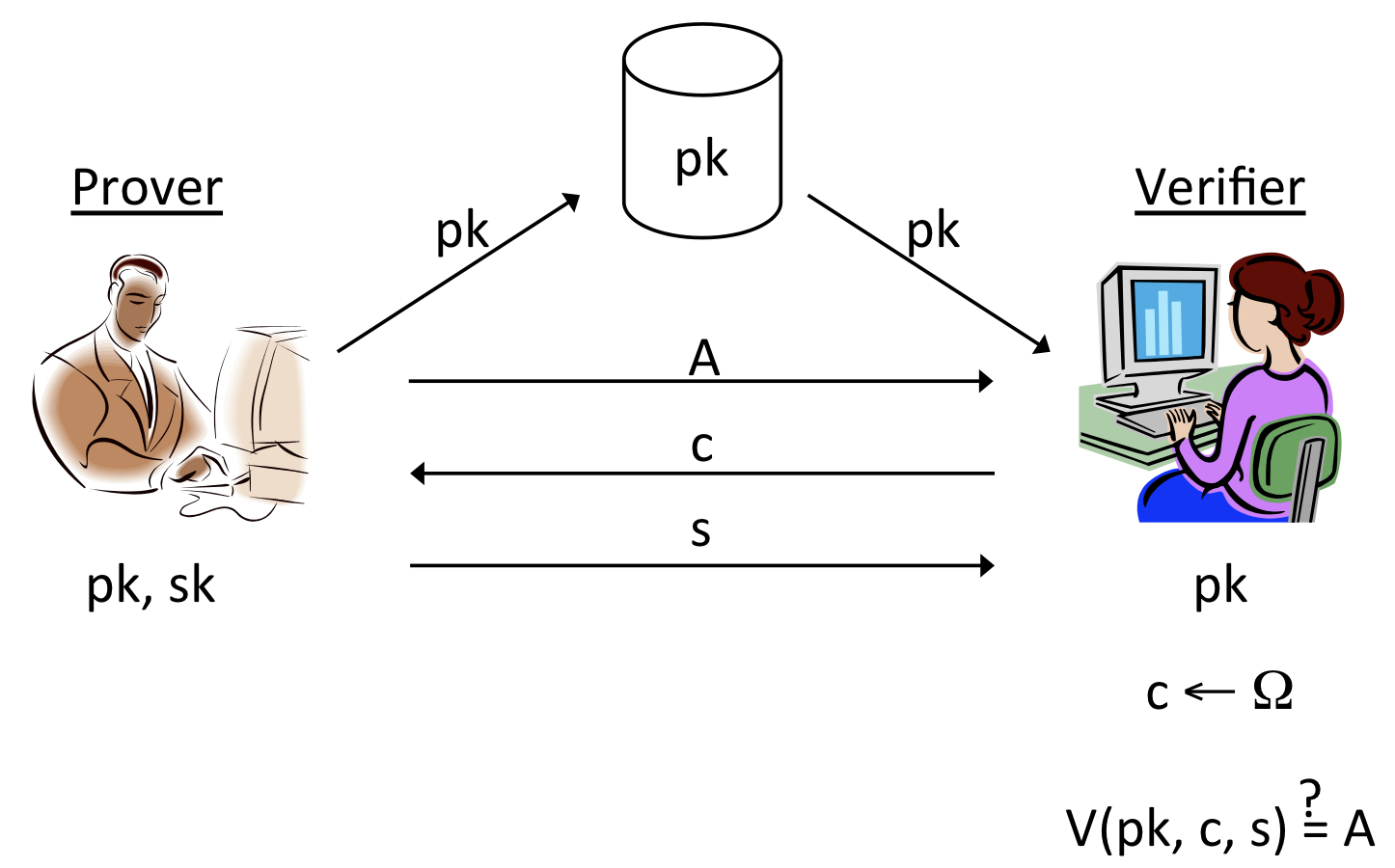
위 그림으로 과정을 살펴봅시다. Prover Peggy와 verifier Victor가 있고, digital signature에서 봤던 scheme처럼 public-key 암호를 기반으로 한 세팅을 전제로 합니다. 그럼 두 사람은 Peggy의 public key를 공유하고 있겠죠? 이때 Peggy의 목표는 해당 공개키가 자신의 것이라는 것을 Victor에게 증명하는 것입니다. 이 증명은 interactive proof를 기반으로 합니다. 즉, 두 당사자는 어떠한 상호작용을 주고받으며 identification scheme을 진행할 수 있어야 합니다.

그럼 어떻게 상호작용이 이루어지는지 알아보겠습니다. 먼저 Peggy는 본인이 보내고 싶은 메시지 $A$를 verifier인 Victor에게 전송합니다. Victor는 challenge에 해당하는 새로운 메시지 $c$를 $\Omega$로부터 uniform하게 뽑아 Peggy에게 전송합니다. 이 challenge에 대하여 Peggy는 본인이 처음에 보낸 메시지 A와 private-key $sk$를 기반으로 $s$를 만들어 Victor에게 전송합니다. 이를 받은 Victor는 $V(pk,c,s)$의 결과값이 $A$가 나오는지 확인하여 전송자가 Peggy인지 확인합니다.

| Security

Identification scheme의 안전성을 살펴봅시다. Identification scheme은 수동적인 공격, 즉 도청만을 가정하여 안전성을 측정합니다. 즉 아무리 도청을 해도 이를 통해 유효한 private key에 대하여 유효한 증명 $s$를 위조할 능력이 없습니다. 또한 이 scheme은 non-degerate 를 가정하고 있는데, 이는 첫 메시지 $A$가 repeating될 확률이 negligible하다는 것을 표현하기 위함입니다.

| Prototypical application

위 과정이 실제 응용되는 예시는 대면 확인, 즉 door access가 있습니다. 만약 스마트 카드를 들고 문을 열고 들어가려 한다면, 스마트 카드에 있는 개인 키로 소유자가 자신임을 보이고, 이를 문에 열결된 카드 리더가 verifier 역할을 함으로써 전체 과정이 수행됩니다. 즉, 신분증과 비슷한 역할을 하고 있습니다.
여기서 어떤 프로토콜을 예시로 들지 않고 신분증과 같은 스마트 카드를 예로 든 이유는 인터넷 상에서의 신분 인증에 위 scheme이 사용되기는 적절하지 않기 때문입니다.

2. Fiat-Shamir transform (피아트-샤미르 변환)

위와 같은 Identification scheme(사용자 인증 프로토콜)에 착안하여 signature를 만들어 봅시다. Identification scheme을 signatuer로 변환하는 시도를 한 첫 번째 사람들이 Fiat와 Shamir였습니다. 이 둘의 이름을 따 Fiat-Shamir transform이라고 알려져 있습니다.

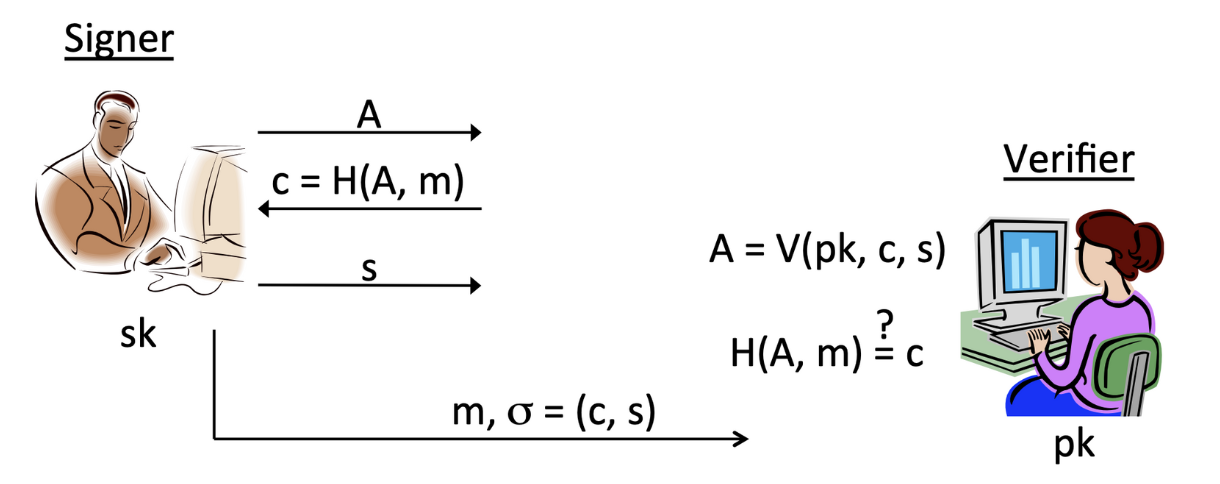
이제 Prover와 Verifier에서, sign을 하기 위해 signer라고 이름을 붙여 이야기해보겠습니다. Signer는 메시지 A에 대하여 자기 자신을 증명하기 위한 sign을 만들지만, 누군가와 상호작용하는 것은 아닙니다. 다만 스스로 scheme을 스스로 돌려 identification에 대한 sign을 만들어냅니다. 과정을 살펴봅시다.

| 과정

1. 초기 메시지 $A$를 scheme에 전달합니다.
2. 앞선 identification scheme에서 verifier가 $c$를 생성하는 방법을 해시함수를 이용하여 초기 메시지 $A$와 자신이 보내고자 하는 메시지 $m$에 대한 다이제스트 $c$를 구현합니다.
3. Signer는 다이제스트 $c$와 자신의 private key를 이용해 서명 $s$를 생성합니다.
4. 생성한 서명 $s$를 verifier에게 전달합니다. 이때 전달하는 메시지 $m$과 서명 $\sigma$는 $(c,s)$로 구성되어 있습니다.
5. Verifier는 검증 알고리즘 $V(pk,\;c,\;s)$를 돌려 그 결과값인 A에 대한 해쉬값이 $c$가 나오는지 확인합니다.

| Security

만약 수동적 공격에 대하여 identification scheme이 안전하고 해시함수 $H$가 랜덤 함수처럼 모델링되어있다면, 여기에서 파생된 signature scheme 또한 안전합니다.

3. Schnorr idenfitication scheme

Schnorr identification scheme은 앞선 identification scheme에서 DLog가 hard problem임에 착안해 만든 프로토콜입니다.

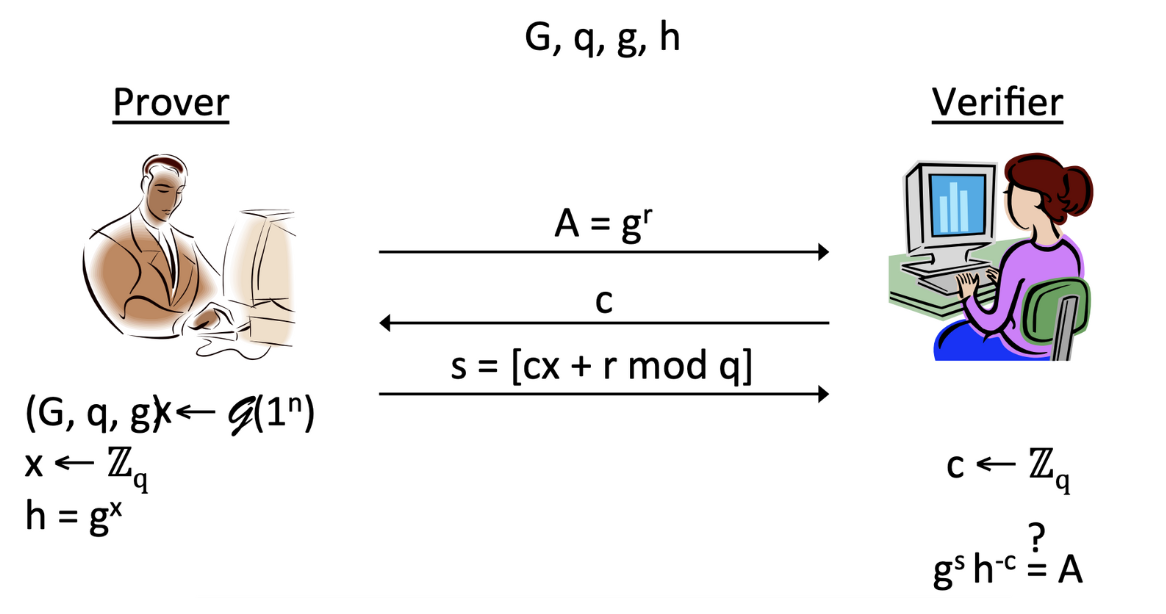
| 과정

0. 먼저 prover가 Group-generation 알고리즘을 이용해 $G$와 $q$, 그리고 generator $g$를 생성합니다. 그룹 내에 랜덤한 값 x를 뽑아 자신의 private key로 세팅합니다. 그리고 $h$를 $g^x$로 만들어, G, q, g, h를 public key로 만듭니다.

1. 이제 interaction proof protocol을 본격적으로 진행합니다. Verifier에게 A = $g^r$ (r은 랜덤한 값)을 전달합니다.

2. Verifier가 public key를 이용해 $c$를 랜덤하게 뽑고 prover에게 전송합니다.

3. 이를 받은 prover는 $c$와 자신의 private key, 그리고 메시지에 대한 정보 $r$을 이용해 서명 $s$를 만듭니다. 이때 $s$는 $s=[cx+r \bmod q]$를 만족합니다.

4. $s$를 전송받은 verifier는 public key에 존재하는 g와 자신이 랜덤하게 준 값 $c$, 그리고 서명 $s$를 이용해 인증이 됐는지 확인합니다. 이때 아래 식에 의해 $g^s h^{-c}=A$가 성립해야 합니다.

| Security

Schnorr signature scheme의 안전성을 살펴봅시다.

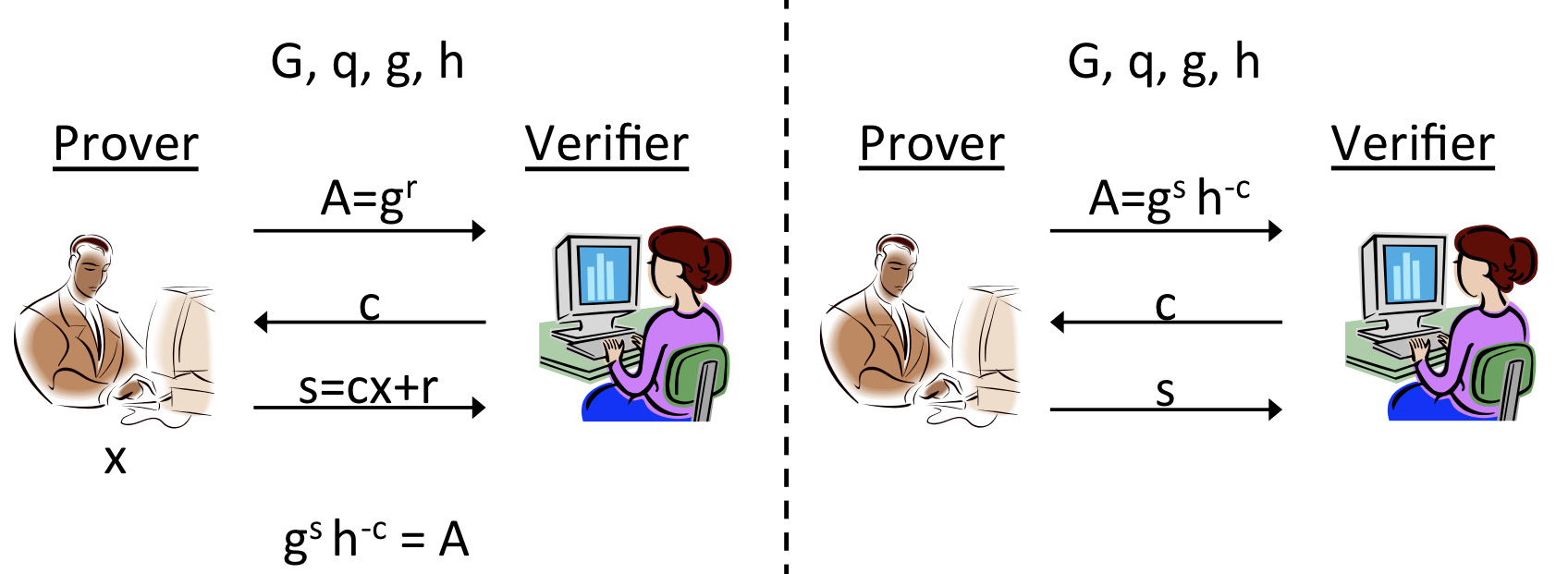
앞에서 본 scheme에서, 우리는 $A = g^r = g^sh^{-c}$임을 보여야했습니다. 왼쪽의 프로토콜은 $x$를 사용하는 프로토콜, 오른쪽은 $x$를 모른 채로 $x$를 이용해 만든 $s$만을 이용하여 $A$를 구합니다. 즉, $x$에 대한 knowlege는 주지 않은 채 verifier에게 $x$에 대하여 증명할 수 있는 scheme인 것입니다.
이는 위에서 정의한 공격자에 대해 Dlog 문제가 어렵다는 것을 바탕으로 secure 하다는 걸 보일 수 있습니다. 그리고 Dlog assumption이 전제가 된 상황에서 H(해시함수)가 random function으로 모델링 되어 있다면, Schnorr signature scheme 또한 secure 하다고 볼 수 있습니다.

4. DSS

DSS는 디지털 서명의 NIST 표준입니다. 여기서 DSA는 Dlog 문제를 이용하여 구현한 것이고, ECDSA는 타원곡선 그룹에 based하여 구현한 것입니다.

3-1 Public-key infrastructure (PKI)

지금까지 signature를 만드는 여러가지 방법에 대해 살펴봤습니다. 이번에도 새롭게 signature가 필요한 경우를 살펴보려고 합니다. 우리가 본 scheme들은 public-key encryption을 기반으로 한 것으로, 두 당사자가 sign을 공유해야 한다면 해당 공개 키를 어디에선가 받아와야 합니다. 하지만 이렇게 받아온 공개 키가 올바른지 아닌지에 대해 검증할 방법이 필요합니다. 이번 강의에서는 Public-key 분배과정에서 배포가 어떤 서명 인프라에 의해 작동하는지 살펴보겠습니다.

1. Public-key distribution

어떤 사용자가 Alice의 공개 키를 가져오고 싶다면, 키가 저장된 데이터베이스에서 Alice의 엔티티에 속하는 공개 키를 찾으면 됩니다. 네트워크를 통해 패킷을 주고 받는 방식인데, 이 과정은 적극적 공격자가 있다고 했을 때 보안에 취약한 문제가 생길 수 있습니다. 만약 어떤 공격자가 동일한 이름인 Alice를 사용해서 자신의 새로운 공개키 $pk'$를 만들었다고 합시다. 데이터베이스 자체에서 Bob에게 공개키가 전달될 땐 공개키를 삽입하는 사람의 신원을 확인할 장치가 없기 때문에 실제 이름이 Alice인지, 해당 사람이 맞는지 확인할 방법이 없습니다.

| Problem 1

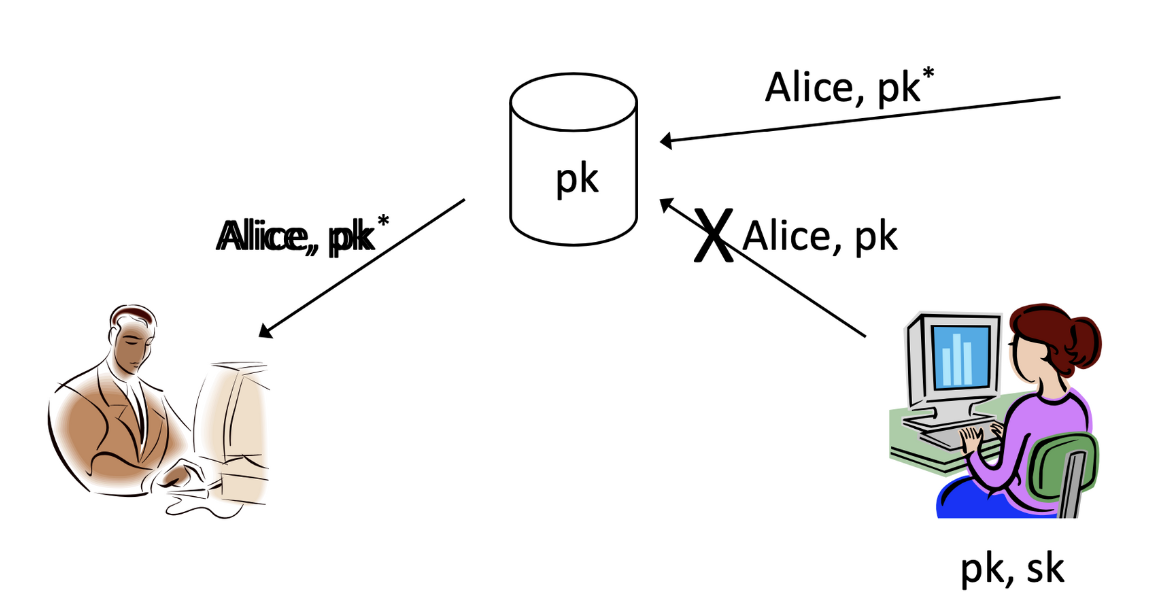
이렇게 $pk'$가 생겼을 때 발생할 수 있는 문제점에 대해 살펴봅시다. 먼저, Alice가 데이터베이스에 도달하지 못하도록 통신을 방해할 수 있습니다. 이렇게 되면, Alice의 이름으로 매칭된 $pk'$라는 위조된 공개 키만을 Bob이 가져갈 수 있게 됨으로써, 상대방은 실제 Alice에 대한 공개키 정보는 절대 얻을 수 없을 것입니다.

| Problem 2

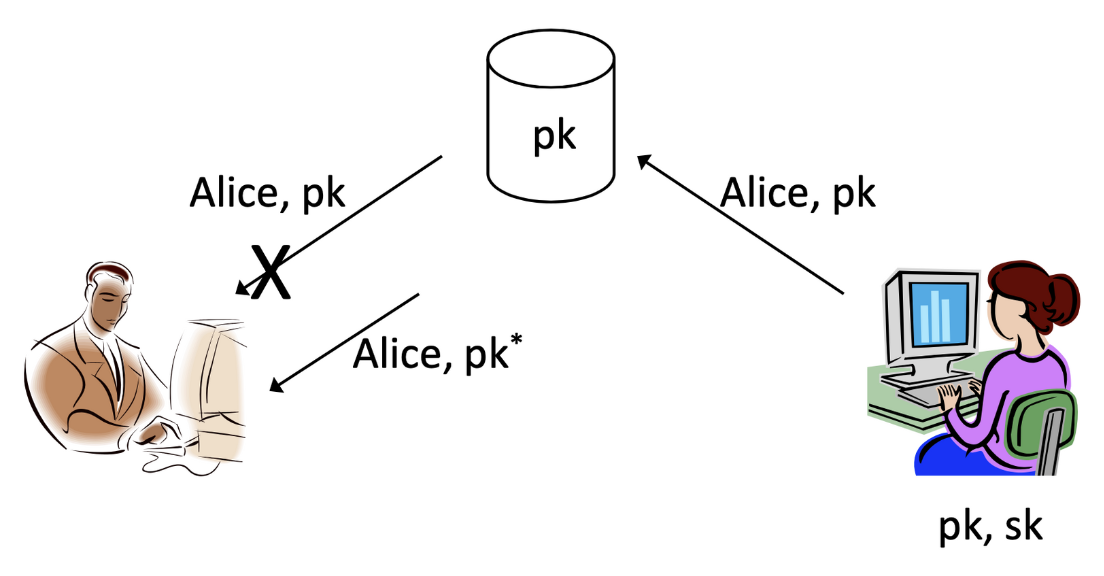
이번엔 Alice가 데이터베이스에 자신의 키를 넣을 수 있지만, 만약 데이터베이스와 Bob의 통신과정을 차단하고 올바른 공개 키 $pk$ 대신 $pk'$를 Bob에게 주입한다면, 어쨌든 Bob은 옳지 않은 공개키를 전달받게 됩니다.

2. Use signatures for secure key distribution!

위와 같은 문제를 해결하기 위해 공개 키를 저장하여 주고받을 때 신뢰를 주는 기반 요소를 만들어야 합니다. 이 신뢰 요소를 trusted party 라고 합니다. 대표적으로 공개 키를 따로 저장해주는 신뢰성이 검증된 민간기업인 CA(Certificate Authority) 가 있습니다. 공공인증기관이라고도 하죠. 우리가 생각하는 공동인증서, 금융인증서 등이 여기에 속합니다.
CA에 속하는 기관들은 본인들의 고유 키를 가지고 있습니다. Public key인 $pk_{CA}$와 private key인 $sk_{CA}$ 가 세팅되어 있죠. 이에 대응하는 공개 키를 모두에게 배포하여 신용가능한 키로 삼습니다.

| 과정

그럼 어떻게 공개 키에 대한 서명이 이루어지는 걸까요? 여기서 자신의 공개 키를 공유하고 싶은 사용자 Alice가 있다고 가정합시다. Alice는 CA에게 자신의 신원에 대한 공개 키 binding에 서명하도록 요청합니다. 이 요청이 승인될 경우, CA에 대하여 인증된 인증서 $cert_{CA \rightarrow Alice}$가 나오고 이는 CA의 비밀키로 Alice에 대한 정보가 서명된 것이므로 $Sign_{sk_{CA}}(Alice, pk)$와 동일합니다.
Alice의 공개키에 대한 정보를 알고 싶은 Bob이 어떻게 Alice의 공개 키에 접근하는지 확인해 봅시다. Bob은 Alice의 공개키와 함께 인증서를 복사하여 발급받을 수 있습니다. 그리고 이 인증서에 대한 서명 검증을 진행하는데, Alice에게 받은 공개 키와 CA로부터 받은 인증서 Sign을 통해 $Vrfy_{pk_{CA}}((Alice, pk), cert_{CA \rightarrow Alice}) = 1$인지 검증을 거칩니다.

3. Chicken-and-egg problem?

하지만 여기서도 문제가 있습니다. Bob이 CA의 서명이 올바른지 확인하기 위해서는 CA의 공개 키도 알아야 합니다. 그렇다면 이 공개 키는 어떻게 알아내야 할까요? Alice의 공개 키를 알기 이전에, CA의 공개 키를 알아내는 과정에서 동일한 문제가 생길 수 있습니다. 이 때문에 Chicken-and-egg problem이 발생합니다. 닭이 먼저냐 달걀이 먼저냐에 대한 인과관계가 명확하지 않은 것이죠.

| Root of trust

이러한 생각을 해결한만한 생각 모델 몇 가지를 소개하겠습니다. 첫 번째는 최상단에 완전히 신뢰 가능한 신뢰의 root가 있다고 가정하는 것입니다. 실제로, 웹사이트에 대한 신뢰 가능한 공개키 목록이 있을 때 그 키를 서명하는 수단을 찾아 올라가다보면 가장 처음 인증이 이루어지는 어떤 key가 존재할테고, 그 키는 완전히 신뢰한다고 가정하는 것입니다. 하지만 어떤 키가 CA의 키인지 정확하게 파악하기 힘든 경우가 많습니다. 그리고 CA를 위한 CA를 위한 CA도 존재하기 때문에 신뢰의 root를 찾는 것은 더더욱 어려운 일이죠.

| Web of trust

또 다른 생각 모델은 web이라는 하나의 신뢰 네트워크 내에서만 인증이 이루어지는 방법입니다. 만약 친구들과 직접 만나 공개 키를 주고받는다면, 그 친구를 신뢰한다고 가정했을 때 서로가 서로의 공개 키에 대하여 해당 키가 맞다는 것을 인증하는 셈입니다. 만약 A가 B의 공개 키인 $pk_B$를 알고 있다고 하면, B는 C로부터 인증서를 받아 A에게 전달하는 것입니다.

| Public-key repository

마지막 해결책은 공개 키 저장소를 갖는 것입니다. 맨 처음 공개 키를 저장하는 하나의 데이터베이스를 가정했었죠? 이 공개 저장소를 확장하여 공개 키 뿐만 아니라 인증서도 함께 저장하는 겁니다. 이렇게 되면 어떤 적극적인 공격자가 $pk'$를 만들기 위해서는 이에 대한 신원 확인이 필요하므로 위조하기가 상당히 어려울 것입니다. 이에 대한 대표적인 예시가 MIT PGP keyserver입니다. 실제로 해당 웹페이지에서는 누군가의 공개 키를 누구나 알아볼 수 있게 찾을 수 있고, 여기 올라온 공개키라면 이미 인증을 받은 것이니 신뢰하고 사용할 수 있겠죠.

3-2 Putting it all together : SSL/TLS

지금까지 비대칭 키 암호화 방식을 기반으로, 키 분배의 기본이 되는 PKI의 작동원리를 공부했습니다. CA를 통해 인증서를 발급받아 신원에 서명을 더하는 방식을 배웠는데요, 만약 이러한 인증서가 네트워크 상에 패킷으로 전달된다면 해당 네트워크 데이터가 제대로 암호화되어야만 공격자의 위협으로부터 벗어날 수 있을 것입니다. 실제 암호화 세계에서 가장 흔히 사용되는 네트워킹 암호화 방식으로, 지금까지 전 코스에서 배운 내용을 합하여 공부해 봅시다. 그럼 본격적으로 네트워크 상에서 사용되는 암호화 방식인 SSL/TLS 프로토콜에 대해 살펴보겠습니다.

1. SSL(Secure Socker Layer)/TLS(Transport Layer Security)

SSL(Secure Socker Layer)/TLS(Transport Layer Security)는 웹브라우저에서 https의 connection 방식으로 사용되는데, 크게 두 가지 phases로 구성되어 있습니다.

2. Handshake protocol

첫 번째 단계는 handshake protocol입니다. 이는 클라이언트와 서버를 연결할 때 두 entities 간에 shared key를 설정하는 프로토콜 방식입니다.

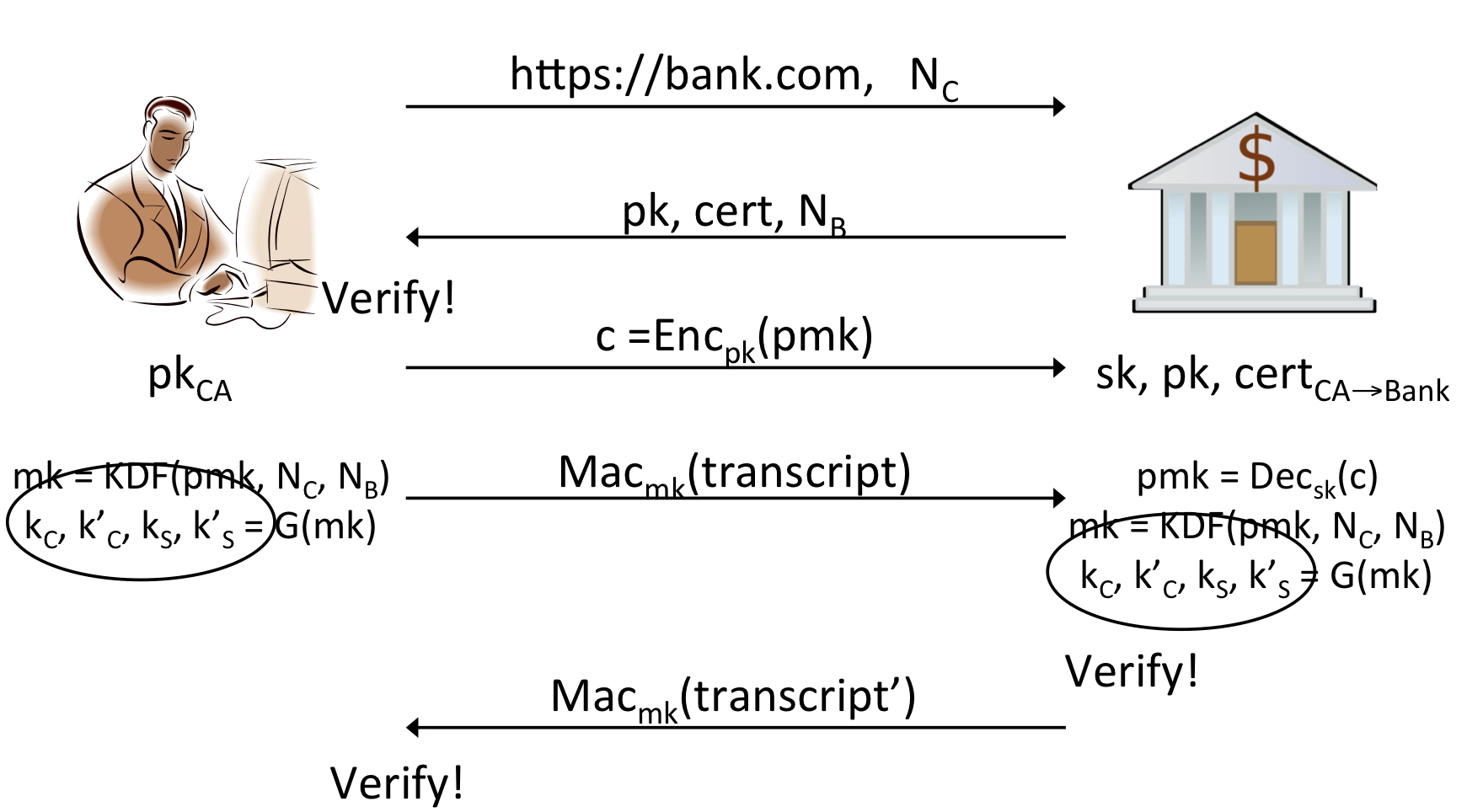
위 그림은 handshake protocol을 이용한 방식을 설명하고 있습니다. 화살표 순서대로 과정을 하나씩 확인해 보겠습니다.

1. 그림의 왼쪽에 있는 유저는 https 프로토콜을 이용하여 url을 통해 은행에 접속합니다. 은행 서버는 url과 유저 메시지 $N_C$를 받아와 은행에 전달합니다.
2. 은행의 공유 키 전송 및 검증 : 은행 서버는 자신의 public key $pk$와 CA로부터 받은 인증서 $cert$, 그리고 서버 메시지 $N_B$를 유저에게 전송합니다. 유저는 이렇게 받은 $cert$를 이용해 은행 서버가 보낸 public key가 진짜 은행 서버의 public key가 맞는지 검증하는 과정을 거칩니다.
3. premaster key 생성 : 은행 서버의 public key라는 것이 확인되면, 유저는 임의의 랜덤값 $pmk$를 생성하고, 그 값을 은행 서버의 public key로 암호화한 $c$를 은행에 전송합니다.
4. 키 교환 : 은행 서버는 자신의 private key를 이용해 이를 복호화 할 수 있고, 이 과정을 거쳐 $pmk$를 알아낼 수 있습니다.
5. 키 검증 : 위 과정을 거치면 두 당사자간 $pmk$, $N_C$, $N_B$가 공유될 것입니다. 이렇게 공유된 세 파라메터를 KDF 알고리즘으로 돌리면, secret parameter 값인 $mk$를 만들 수 있습니다. 그리고 다시 한 번 $mk$와 MAC 알고리즘을 이용해 각자의 transcirpt의 태그가 verify한지 양쪽 모두 확인합니다.
6. 공유 키 생성 : 검증된 $mk$를 key generator 알고리즘 $G$에 넣습니다. 그럼 두 당사자는 알고리즘의 결과값 $k_c, k'_c, k_s, k'_s$ 를 공유하게 됩니다.
   
   

3. Record-layer protocol

두 번째 단계는 record-layerp protocol입니다. 앞서 공유 키인 $k_c, k'_c, k_s, k'_s$가 생성되었습니다. Record-layer protocol은 이 공유 키를 통해 secure communication을 진행하는 방식입니다.
여기서 $k_c, k'_c$ 는 클라이언트가 encrypt/authenticate 할 때 사용되는 키이고, $k_s, k'_s$ 는 서버가 메시지에 대하여 encrypt/authenticate를 진행할 때 사용되며, 정보 교환의 순서를 매겨 sequence number를 준다면 replay attack을 막을 수 있습니다.