[퀵정렬]

퀵정렬

기준 원소를 하나 잡아 기준 원소보다 작은 원소와 큰 원소 그룹으로 나눠, 기준 원소의 좌우로 분할한 다음 각각을 정렬하는 방식이다. 평균적으로 가장 좋은 성능을 가져, 가장 많이 쓰이는 정렬 알고리즘이다.

[31, 8, 48, 73, 11, 3, 20, 29, 65, 15]

1) 기준 원소를 15로 잡는다는 전제하에, 15을 중심으로 이보다 작은 원소들은 15의 왼쪽에, 나머지 원소들은 15의 오른쪽에 재배치한다.

[8, 11, 3, ((15)), 31, 48, 20, 29, 65, 73]

2) 왼쪽과 오른쪽에 위치한 원소들을 독립적으로 정렬한다.

[3, 8, 11, ((15)), 20, 29, 31, 48, 65, 73]

3) 결론적으로 크기가 섞이지 않는 두 배열을 나눠놓고 양쪽 배열을 재귀적으로 정렬하는 특징을 갖는다.

분할의 작동 과정

---

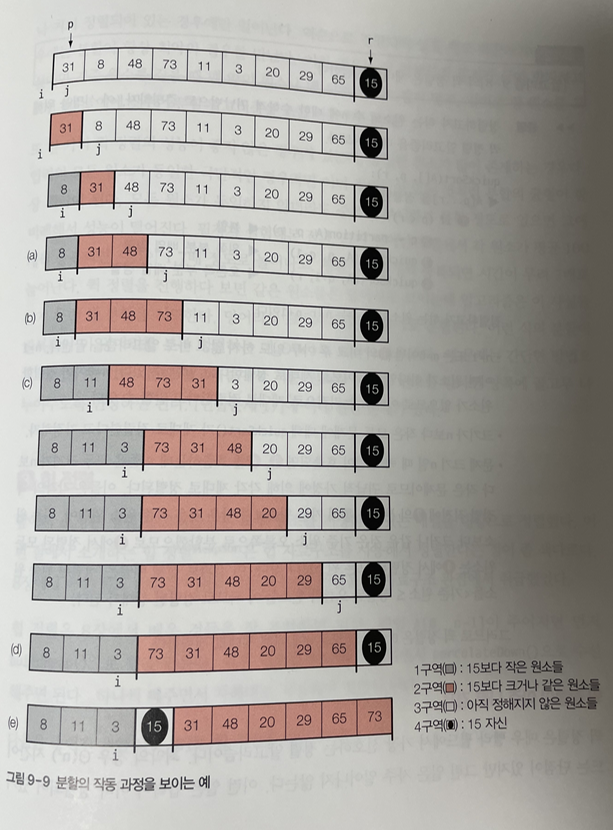
퀵 정렬의 장점 및 단점

장점

1. 특정 상태가 아닌 이상 평균 시간 복잡도는 NlogN이며, 다른 NlogN 알고리즘에 비해 대체적으로 속도가 매우 빠르다.

2. 추가적인 별도의 메모리를 필요로하지 않으며 재귀 호출 스택프레임에 의한 공간복잡도는 logN으로 메모리를 적게 소비한다.

단점

1. 특정 조건하에 성능이 급격하게 떨어진다.

   • 크기가 1억인 정렬에서 각 원소가 평균 100개씩 중복되면 시간이 1.7배로 늘어나고, 평균 1000개씩 중복되면 시간이 7배로 늘어난다.
   • 이미 정렬되어 있거나, 거의 정렬되어 있는 경우, 역순으로 정렬되어 있는 경우 최악의 경우에 해당된다.
     - 해당 경우에서, 분할 과정에서 pivot을 선택할 때 최소값이나 최대값을 선택하는 경우가 발생할 가능성이 높다.
     이 경우, 분할된 두 개의 부분 배열 중 한 쪽이 매우 작아져서 퀵 정렬의 장점을 활용하지 못하고,
     다른 한 쪽은 대부분의 원소를 가지고 있어서 분할 과정에서 많은 비교와 교환이 필요된다.

2. 재귀를 사용하기 때문에 재귀를 사용하지 못하는 환경일 경우 그 구현이 매우 복잡해진다.

구현 코드

public class QuickSort {

    public static void main(String[] args) {
        int[] arr = {31, 8, 48, 73, 11, 3, 20, 29, 65, 15};
        printArray(arr, arr.length); // 정렬 전 배열 출력
        System.out.println();
        quickSort(arr); // 퀵정렬 수행
        System.out.println();
        printArray(arr, arr.length); // 정렬 후 배열 출력

    }

    // 퀵정렬 함수 호출을 위한 Wrapper 함수
    private static void quickSort(int[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    // 퀵정렬 함수
    private static void quickSort(int[] arr, int start, int end) {
        // pivot을 중심으로 분할한 뒤, 분할된 배열에 대해 퀵정렬 함수를 재귀적으로 호출한다.
        int part2 = partition(arr, start, end);

        if (start < part2 - 1) {
            quickSort(arr, start, part2 - 1);
        }
        if (part2 < end) {
            quickSort(arr, part2, end);
        }
    }

    // pivot을 중심으로 분할하는 함수
    private static int partition(int[] arr, int start, int end) {
        // pivot은 배열의 중간값으로 선택한다.
        int pivot = arr[(start + end) / 2];

        // start와 end를 이용하여 pivot보다 큰 값과 작은 값으로 나눈다.
        while (start <= end) {
            while (arr[start] < pivot) start++;
            while (arr[end] > pivot) end--;
            if (start <= end) {
                // start와 end의 값을 swap해준다.
                swap(arr, start, end);
                start++;
                end--;
            }
        }
        // 분할된 배열 중, 왼쪽 파트의 끝 지점을 리턴한다.
        return start;
    }

    // 배열의 두 요소를 swap해주는 함수
    private static void swap(int[] arr, int start, int end) {
        int temp = arr[start];
        arr[start] = arr[end];
        arr[end] = temp;
    }

    // 배열을 출력하는 함수
    private static void printArray(int[] arr, int size) {
        for (int cnt = 0; cnt < size; cnt++) {
            System.out.print(arr[cnt] + " ");
        }
        System.out.println();
    }

}