[백준] 1074 : Z (JAVA/자바)

문제

BOJ 1074 : Z - https://www.acmicpc.net/problem/1074

풀이

딱 봤을 때 재귀로 풀이하면 되겠다! 했는데 바로 메모리 초과가 나버렸다. 이유를 분석해보니, n이 최대 15이기 때문에 최대 2^15의 row와 col이 생길 수 있다. 그래서 전체를 재귀로 탐색하면 메모리초과나 시간초과가 발생한다.

문제에서는 좌표(r,c)가 몇번째에 방문되는지 만 알아내면 되기 때문에, 굳이 좌표(r,c) 범위 밖의 영역은 재귀호출하지 않아도 된다.

이분탐색을 적용해서 풀이해야 한다. 이분탐색이란, 원하는 탐색범위를 두 부분으로 분할해서 찾는 방식이다. 이 문제에서는 4분탐색(?)이 되겠다.

4분할로 나눈 뒤, (r,c)가 존재하는 범위만 재귀 탐색을 진행한다. 아래 코드의 recursive() 함수가 재귀 호출을 진행하는데, 시작점과 length가 파라미터로 주어지면, 이 값을 통해 4개 영역으로 나눌 수 있다.

예시를 살펴보자. n이 3이라면 다음과 같은 결과를 나타내야한다.

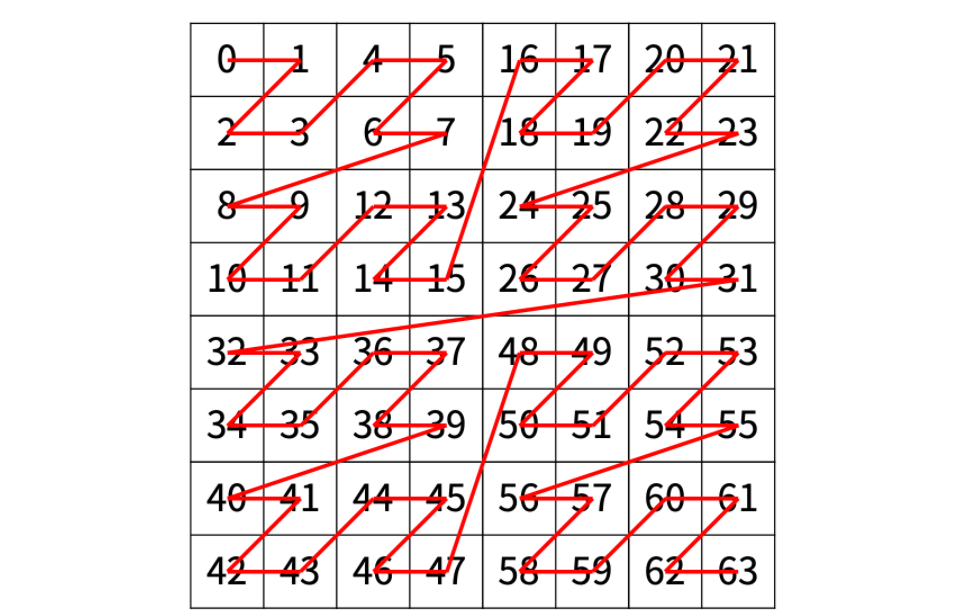
첫 재귀호출의 파라미터로는 시작점은 (0,0), 길이가 8로 호출된다. 이 이차원 배열을 4분할 하면, 아래와 같이 나눌 수 있다.

• (0,0)부터 시작해서 length 4, 카운트는 0부터 시작
• (0,4)부터 시작해서 length 4, 카운트는 16부터 시작
• (4,0)부터 시작해서 length 4, 카운트는 32부터 시작
• (4,4)부터 시작해서 length 4, 카운트는 48부터 시작

여기서 (r,c)가 (3,1)이라면 첫번째 영역만 탐색하면 되고, (5,5)라면 네번째 영역만 탐색하면 되는 것이다! 카운트 정보는 계속 더해주며 재귀를 호출한다.

최종적으로 length가 2일 때 count를 센다. r,c를 만난다면 count를 출력하고 종료한다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int r;
    static int c;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] inputs = br.readLine().split(" ");

        int N = Integer.parseInt(inputs[0]);
        r = Integer.parseInt(inputs[1]);
        c = Integer.parseInt(inputs[2]);

        int pow_n = (int) Math.pow(2, N);


        recursive(0,0, pow_n, 0);

    }

    public static void recursive(int si, int sj, int length, int cnt){ // si, sj는 시작점
        if(length==2){
            for (int i = si; i <= si+1; i++) {
                for (int j = sj; j <= sj+1; j++) {
                    if(i==r && j==c){
                        System.out.println(cnt);
                        return;
                    }
                    cnt++;
                }
            }
            return;
        }

        int half = length/2;

        // si, sj, half, cnt
        // si, sj+half, half, half*half*2
        // si+half, sj, half, half*half
        // si+half, sj+half, half, half*half*3

        if(si<=r && r<si+half && sj<=c && c<sj+half){
            recursive(si, sj, half, cnt);
        }else if(si<=r && r<si+half && sj+half<=c && c<sj+length){
            recursive(si, sj+half, half, cnt+half*half);
        }else if(si+half<=r && r<si+length && sj<=c && c<sj+half){
            recursive(si+half, sj, half, cnt+half*half*2);
        }else{
            recursive(si+half, sj+half, half, cnt+half*half*3);
        }
    }
}

정리

✔ 알고리즘 분류 - 분할 정복, 재귀
✔ 난이도 - ⚪ Silver 1

🤦‍♀️ 오늘의 메모

• 재귀호출은 간단(?)하지만 메모리나 시간에 아주 효율적인 방법은 아니다. 문제의 조건을 보고 호출 건 수를 줄일 수 있다면 조건을 걸어 처리할 것!
  
  
  

참고 사이트

딱히 없음