[백준] 6588 - 골드바흐의 추측 (JAVA)

흶·2021년 6월 27일

Algorithm

목록 보기

2/60

문제

BOJ 6588 : 골드바흐의 추측 - https://www.acmicpc.net/problem/6588

풀이

시간초과 때문에 속썩인 문제. 테스트 케이스가 짝수 정수 n (6 ≤ n ≤ 1000000)이기 때문에, 일반적인 prime number 구하는 식을 세우면 시간초과가 난다. 그래서 검색해봤더니 에라토스테네스의 체 라는 개념을 사용한다고 한다.

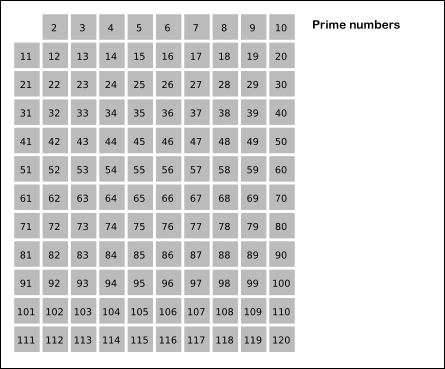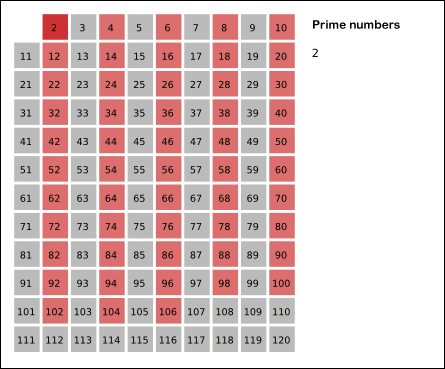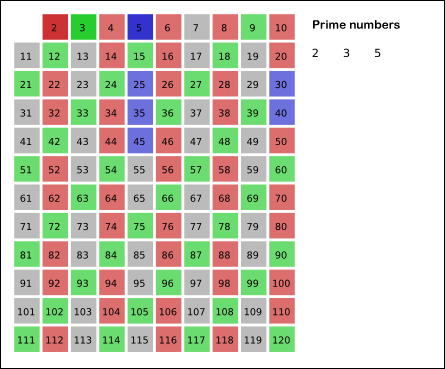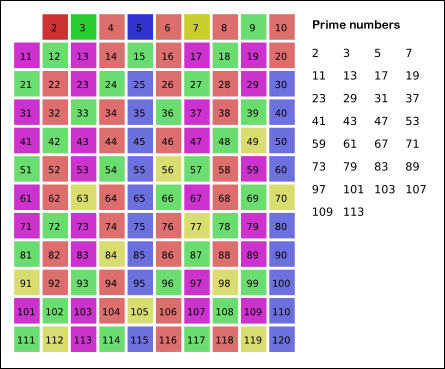
[에라토스테네스의 체]
"k=2 부터 √N 이하까지 반복하여 자연수들 중 k를 제외한 k의 배수들을 제외시킨다."

간단히 순서를 살펴보자면,
1. 소수를 판별할 범위만큼 배열을 할당한다.
2. 해당하는 값으로 배열을 초기화한다.
3. 이후에 하나씩 지워나간 후 최종적으로 지워지지 않은 수가 prime number이다.

아무튼 이렇게 소수인지 아닌지 1,000,000까지 미리 계산해둔 뒤, 입력받는 테스트 케이스에 대해 두 홀수 소수의 합으로 나타낼 수 있는지 판단하면 된다.

두 홀수 소수의 합으로 나타낼 수 있는지 여부는 for문 사용해서 확인한다. 예를 들어, n이 12이면 1-11 2-10 3-9 4-8 ... 이런식으로 나눠보면서 두 수가 모두 소수인지 판별해서 가장 차이가 큰 수를 출력했다. (짝수라면 소수가 아니기 때문에 따로 짝수 여부를 걸러주지는 않았다.)

n = a + b의 형태로 나타낸다면 a가 작을수록 당연히 b-a의 값이 커지기 때문에 a, b가 모두 홀수 소수라면 for문을 중단하고 return 해준다.

코드

성공한 코드

import java.io.*;

public class Main {

    static boolean[] prime_nums;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        primeNumberEratosthenesSieve();

        while(true) {
            int n = Integer.parseInt(br.readLine());
            if(n==0) break;

            int result = isPossible(n);

            if(result>0){
                bw.write(n+" = "+result+" + "+(n-result)+"\n");
            }else{
                bw.write("Goldbach's conjecture is wrong.");
            }
        }
        bw.flush();
    }

    public static int isPossible(int n){
        for(int i=1; i<=n/2; i++){
            int a = i;
            int b = n - i;
            if(prime_nums[a] && prime_nums[b]) return a;
        }
        return -1;
    }

    public static void primeNumberEratosthenesSieve() {
        prime_nums = new boolean[1000001];

        // initialize
        for(int i=2;i<=1000000;i++) {
            prime_nums[i] = true;
        }

        for(int i=2;i<=1000000;i++) {
            if(!prime_nums[i]) continue; // 이미 지워진 수라면 pass

            // 이미 지워진 숫자가 아니라면, 그 배수부터 출발하여 가능한 모든 숫자 지우기
            for(int j=2*i;j<=1000000; j+=i) {
                prime_nums[j] = false;
            }
        }
    }
}

시간초과 난 코드

import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        while(true) {
            int n = Integer.parseInt(br.readLine());
            if(n==0) break;

            int result = isPossible(n);

            if(result>0){
                bw.write(n+" = "+result+" + "+(n-result)+"\n");
            }else{
                bw.write("Goldbach's conjecture is wrong.");
            }
        }
        bw.flush();
    }

    public static int isPossible(int n){
        for(int i=1; i<n/2; i++){
            int a = i;
            int b = n - i;
            if(isPrimeNum(a) && isPrimeNum(b)) return a;
        }
        return -1;
    }

    public static boolean isPrimeNum(int n){
        if(n<=1) return false;
        for(int i=2; i<n; i++){
            if(n%i==0){
                return false;
            }
        }
        return true;
    }
}

이렇게 n의 범위는 생각도 안하고 그냥 원래 잘 풀던 방식으로 풀면 시간초과가 난다.

정리

✔ 알고리즘 분류 - 수학, 정수론, 소수 판정, 에라토스테네스의 체
✔ 난이도 - ⚪ Silver 1

🤦‍♀️ 오늘의 삽질리스트

아직도 n의 범위를 보고 시간초과가 날 지 안날 지 판단하는게 어렵다. 시간초과 난 코드를 보면 isPossible()에서 O(n), isPrimeNum()에서 O(n) 해서 전체 시간복잡도는 대략적으로 O(n^2). n이 최댓값이 1,000,000이기 때문에 n^2하면 10^12정도,,,ㅎ 10^9 정도가 1초라고 보면 아ㅏㅏ주 많이 넘어간다. 당연히 시간초과...
새로운 개념을 습득하다 보니 이해하는 데에 시간이 조금 걸렸다. 소수를 판별하는 기법 중 하나인 에라토스테네스의 체 개념을 확실하게 알게되었다.

소수를 판별하기 위한 알고리즘이며, 대량의 소수를 판별할 때 미리 소수인지 아닌지 구해놓은 후 가져다 쓰는 방법으로 시간복잡도를 줄인다. ~~항상 알고 보면 별거 아닌데 왜 처음 접하면 그렇게 어려운지 모르겠다.~~
그리고 처음에 참고했던 글에서는 int[] 자료구조를 써서 값을 정수로 초기화하고, 지울 경우 0으로 값을 대입하여 0이 아닐 경우 소수이다 이렇게 판단했다.

이걸 그냥 값이 0보다 크면 소수임 이렇게 생각하면 될 것을 굳이 ArrayList를 하나 만들어서 하나하나 넣어놓고 isContain()으로 소수인지 판별하는 삽질을 했다. ~~어쩐지 에라토스테네스 썼는데도 시간초과 나더라.~~

나중에는 boolean[]으로 만들어서 True/False로 판별해서 풀긴 했지만, 풀기 전에 자료구조를 어떻게 쓰면 편할지 한번 더 생각을 하자!