문자열 검색 알고리즘

문자열 검색 알고리즘은 문자열을 다루는 알고리즘의 하나로, 특정 문자 또는 문자열을 더 큰 문자열이나 글에서 찾아내는 수법이다.
문자열 검색 알고리즘 - 위키백과

문자열 검색은 실생활에서 많이 사용되는 만큼 KMP, 라빈-카프, 보이어-무어, 아호-코라식 등의 다양하고 효율적인 방법들이 존재한다.
이번 글에서는 단순한 방법과 KMP 알고리즘에 대해 정리해보고자 한다.

단순한 방법(Brute force)

표준 라이브러리의 구현에 널리 사용됩니다.

- 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 2

주어진 긴 문자열 S가 찾고자 하는 문자열 N을 포함하는지 확인하고, 시작위치를 찾으려 한다.
가장 단순한 방법은 N을 S의 가능한 모든 시작위치를 다 시도해 보는 것이다.
처음에는 S의 0번 글자에서 시작하는 부분 문자열이 N과 같은지 확인하기 위해 하나하나 맞춰나간다.
모든 글자가 일치하면 답에 추가하고, 중간에 실패하거나 답을 하나 찾으면 시작위치를 오른쪽으로 한 칸 옮겨 계속한다.

KMP 알고리즘

검색 과정에서 얻는 정보를 버리지 않고 활용하면 시간을 절약할 수 있다.
위의 예시에서 첫번째 과정을 통해 6개의 글자는 일치했다는것을 알 수 있고, S[i ... i + 5] == "AABAAB"여야 한다. 따라서 S의 i + 1에서 시작하는 N은 일치할 수 없다.
이 사실을 이용하면 시작위치 i ~ i + 5중 일부는 확인할 필요가 없음을 알 수 있다.

KMP 알고리즘이란?

알고리즘을 개발한 Knuth-Morris-Pratt 세명의 이름을 따서 만든 알고리즘으로
KMP 알고리즘은 불일치가 일어났을 때, 지금까지 일치한 글자의 수를 이용하여 불필요한 탐색은 건너뛰고, 비교가 필요한 부분만을 비교하는 알고리즘이다.

다음 시작 위치 찾기

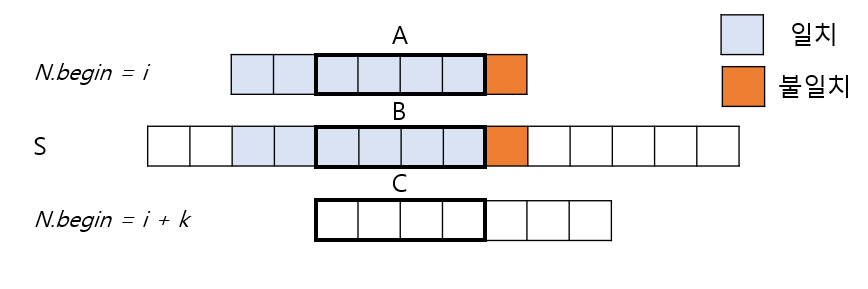
위의 그림에서 i ~ i + 5까지 N과 S가 일치할 때, i + k가 시작지점이 될 수 있는 조건을 알아보자.

1. 하늘색 구역은 일치한 구간이므로 A == B.
2. 시작위치 i + k가 답이 되기 위해서는 B == C이어야 한다.
3. A == B, B == C 두 조건이 만족하므로 A == C이다.
4. 이때 A, C는 N[ ~ matched - 1] 의 접두사/접미사 이다.
   4-1) 길이 matched(일치하는 길이) - k인 접두사와 접미사가 같다면 i + k가 시작위치가 될 수 있다.
   4-2) 위의 그림에서는 2(k)칸 뛰어 넘고 싶다. 이때, S와 N이 일치하는 길이가 6이므로, 접두사와 접미사가 같은 길이는 4이어야 한다.
5. 만약 A != C가 된다면 시작위치 i + k는 정답이 될 수 없으므로 건너뛴다.

접두사, 접미사

여기서 접두사, 접미사는 일반적인 의미와 약간 다르게 사용한다.

• 접두사 : 문자열 S의 0 ~ a번 까지의 글자로 구성된 부분 문자열 S[0 ~ a]를 의미한다.
• 점미사 : 문자열 S의 b번 ~ 끝 까지의 글자로 구성된 부분 문자열 S[b ~ ] 를 의미한다.

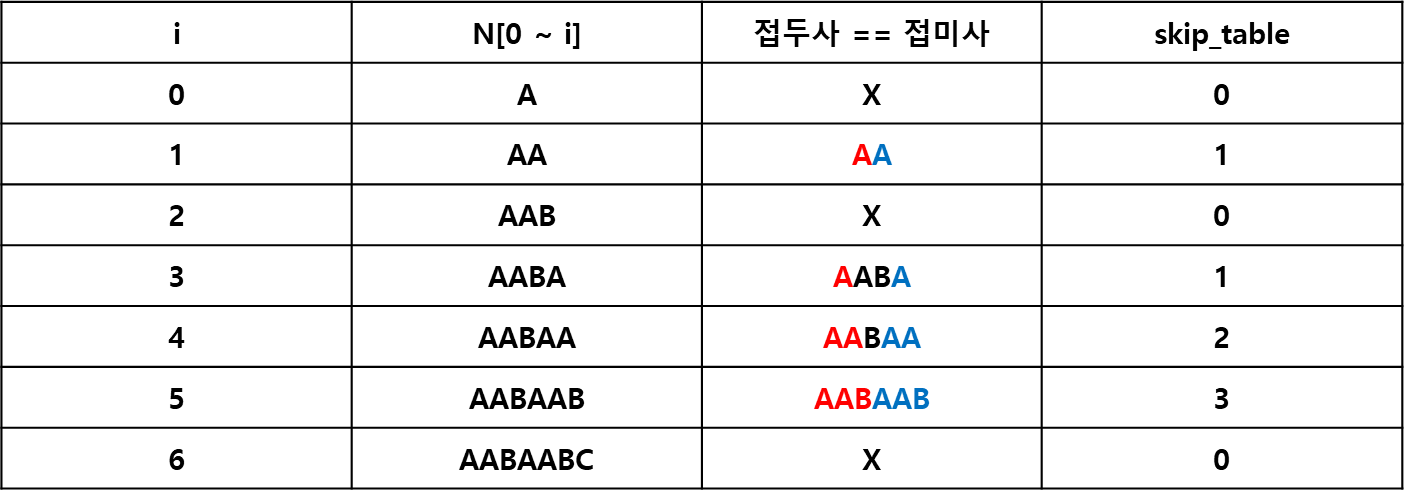
skip_table

skip_table[i] : N[0 ~ i]의 접두사 == 접미사가 되는 문자열의 최대 길이라 할때
N = 'AABAABC의 skip_table을 만든다면

KMP 알고리즘 구현

테이블은 적절한 전처리 과정을 통해 계산했다고 가정한다.
테이블 또한 KMP 구현방법과 유사하게 계산할 수 있다.

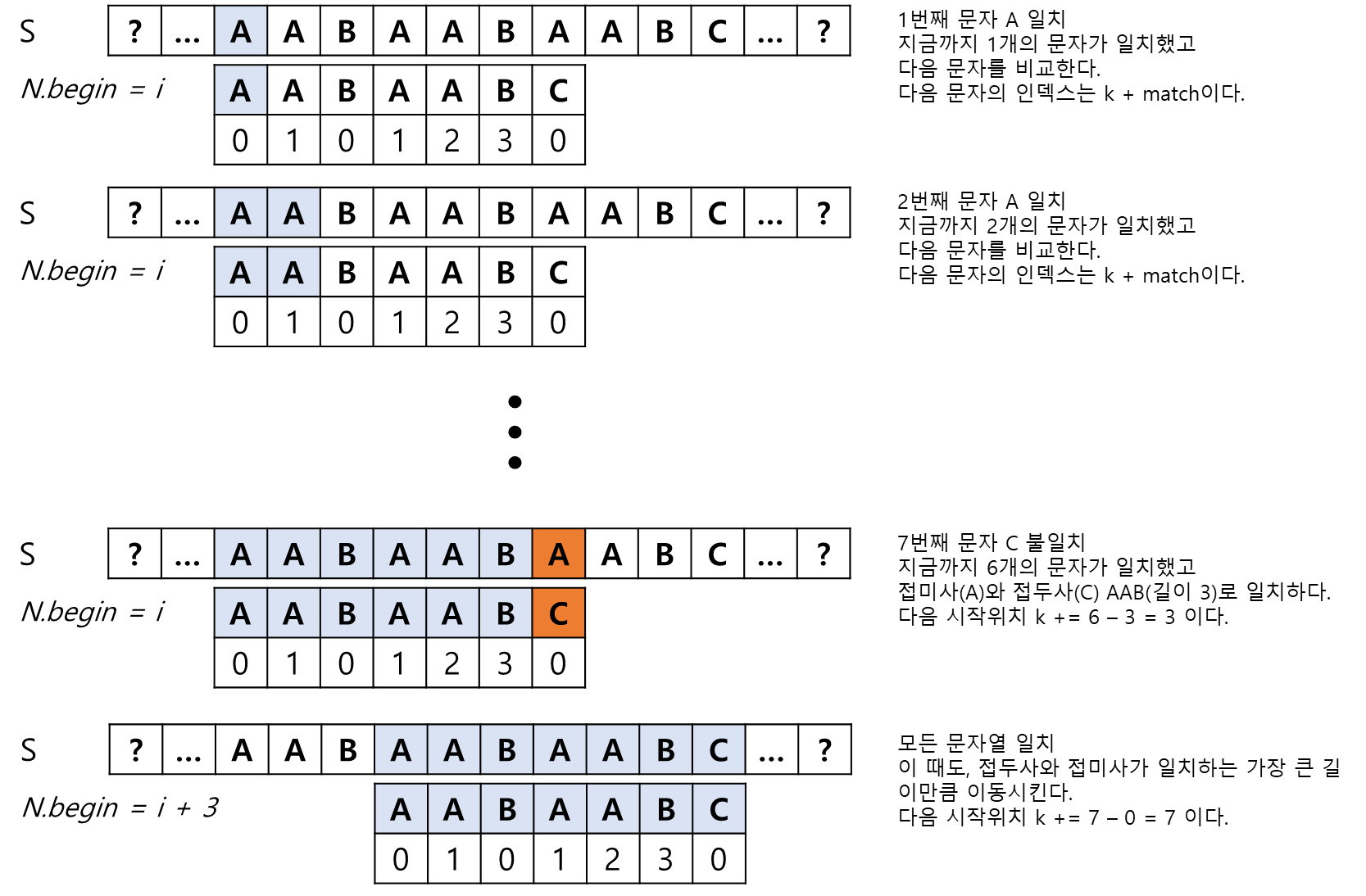
k= 다음 시작 위치, matched = 일치한 문자열 길이, l = 접두사와 접미사가 같은 길이

구현의 편의를 위해 다음 시작 위치 찾기 의 4. 에서 구한 l = matched - k를 k = matched - l로 변경하여 구현한다.
이 때, 시작위치 k는 누적되며 matched의 이전까지의 접두사와 접미사가 같은 길이를 table로 구해두었으므로 이를 이용하여 구현한다.

kmp 구현 코드

def kmp(S, N):
    s_size, n_size = len(S), len(N)
    ret = []
    table = make_table(N)

    # 시작위치 (i + )k, 일치하는 정도 match, 접두사 접미사가 같은 길이 l (table)
    # l = match - k 일 때 i + k는 시작위치가 될 수 있다.
    # k = match - l
    k, matched = 0, 0
    # 시작위치는 (긴 글의 길이) - (찾고자 하는 글의 길이)를 넘어가면 안된다.
    while k <= s_size - n_size:  
        if matched < n_size and S[k + matched] == N[matched]:
            matched += 1
            if matched == n_size:
                ret.append(k)
        else:
            if matched == 0:
                k += 1
            else:
                k += matched - table[matched - 1]
                matched = table[matched - 1]

    return ret

Skip_table 구현

KMP 과정과 유사하다.

k= 다음 시작 위치, matched = 일치한 문자열 길이

구현 코드

def make_table(N):
    n_size = len(N)
    table = [0 for _ in range(n_size)]
    # 시작위치 begin, 일치하는 정도 matched
    begin, matched = 1, 0  # begin = 0 이면 자기 자신을 찾아버린다.
    while begin + matched < n_size:
        if N[begin + matched] == N[matched]:
            matched += 1
            table[begin + matched - 1] = matched
        else:
            if matched == 0:
                begin += 1
            else:
                begin += matched - table[matched - 1]
                matched = table[matched - 1]

    return table

시간복잡도

1. KMP 동작 과정 O(S)
2. Table 제작 과정 O(N)
O(S + N)이다.

참고 사이트

그림으로 알아보는 문자열 검색 알고리즘
KMP 알고리즘