📌 스택 (Stack)
- 데이터가 일렬로 나란히 저장되어있는 선형구조
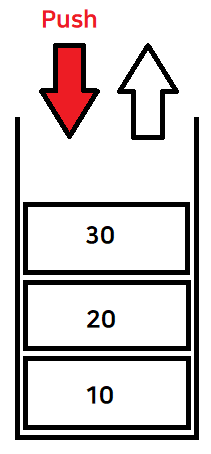
- 마지막에 들어온 데이터가 첫번째로 나가는 LIFO(Last In First Out) 구조 (후입선출 구조)
- 그림을 보면 프링글스 통을 예시로 생각하면 쉽다 (맨 위부터 먹을 수 있고, 아래에 있는 걸 꺼내먹을 수 없다)
- 즉, 가장 마지막에 삽입된 데이터가 처음으로 나가는 구조
- 해당 스택의 구현은 배열로 해보았다
-
class로 스택을 구현
-
T 자료형의 Container[ ]배열을 만들고 안에 값을 초기화
-
스택의 크기를 정할 size 변수
-
데이터를 넣을 자리인 top 변수
-> 🟥 스택은 상단(top)에서만 데이터의 접근이 가능하다. 삽입/삭제도 top에서만 가능
-> 마지막으로 삽입된 요소의 다음 인덱스를 가리키는 변수이기 때문
#include <iostream>
#define SIZE 5
using namespace std;
// 배열로 스택 구현
template <typename T>
class Stack
{
private:
T Container[SIZE];
int size;
int top;
public:
Stack()
{
size = 0;
top = -1;
for (int i = 0; i < SIZE; i++)
{
Container[i] = NULL;
}
}
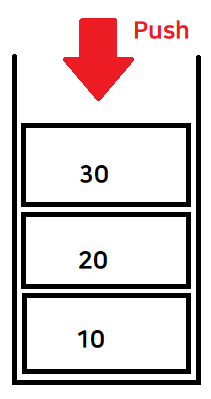
✅ Push( ) 함수 (데이터 넣기)
-
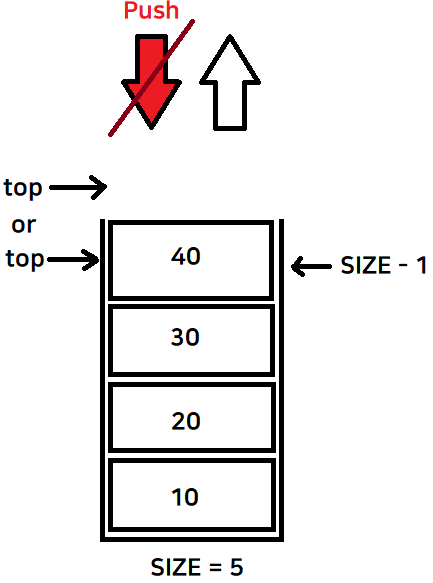
데이터를 넣을 자리인 top이 SIZE - 1보다 크게되면 더이상 데이터를 넣을 수 없음 (스택 오버플로우)
-
Container배열안의 전위증가로 top을 이동시킨 뒤 데이터를 넣음
-
- 데이터를 넣기 전 상태
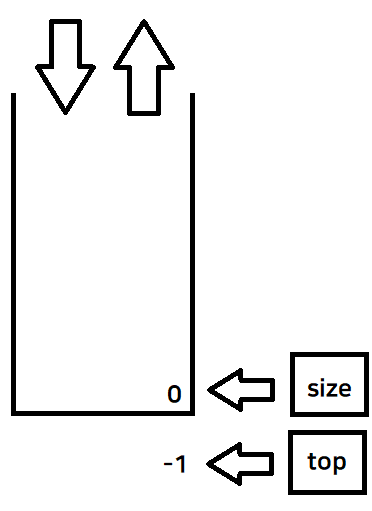
- 데이터를 넣기 전 상태
-
- 데이터를 넣으려면 전위증가 ++top 후 데이터 삽입
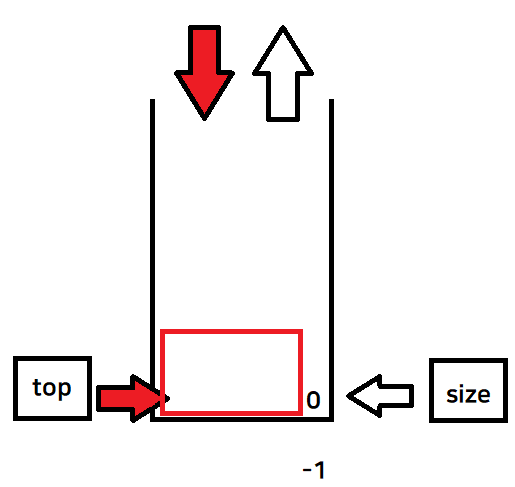
- 데이터를 넣으려면 전위증가 ++top 후 데이터 삽입
void Push(T data)
{
if (top >= SIZE - 1)
{
cout << "Stack OverFlow" << endl;
}
else
{
Container[++top] = data;
}
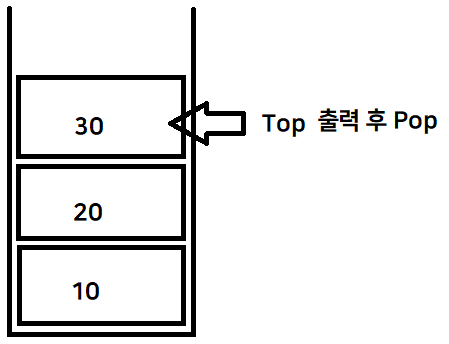
}✅ Pop( ) 함수 (데이터 빼기)
-
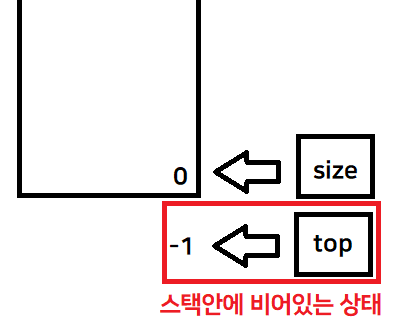
스택안이 비어있는 지 판단하는 bool형 Empty( )함수를 따로 정의
-
bool Empty( ) : top이 -1 보다 작거나 같으면 스택이 비어있는 상태 (시작지점이 -1이기 때문)
-
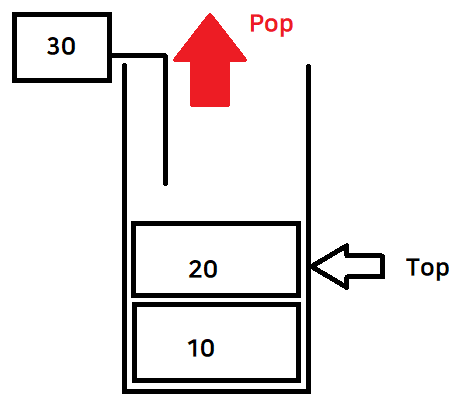
Empty( ) == true인 상태에서 Pop할 수 없다 (뺄 데이터가 없다)
-
스택에 데이터가 있으면 top--
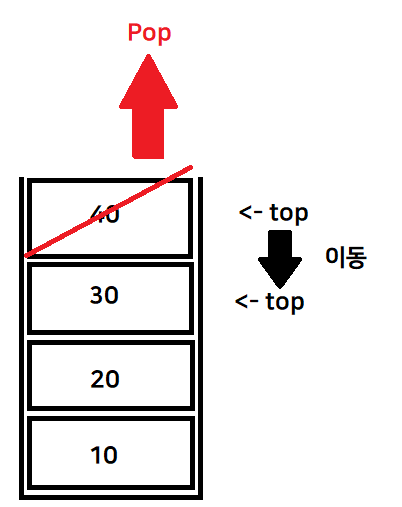
void Pop()
{
if (Empty())
{
cout << "Stack is Empty" << endl;
}
else
{
top--;
}
}
bool Empty()
{
if (top <= -1)
{
return true;
}
else
{
return false;
}
}
✅ top & size 반환
// 가장 꼭대기의 값을 반환
const T& Top()
{
return Container[top];
}
const int& Size()
{
size = top + 1;
return size;
}📌 메인함수
int main()
{
Stack <int> stack;
stack.Push(10);
stack.Push(20);
stack.Push(30);
cout << "Stack의 크기 : " << stack.Size() << endl;
while (stack.Empty() == false)
{
cout << stack.Top() << " ";
stack.Pop();
}
return 0;
}출력값:
스택의 시간복잡도
-
기본적으로 스택의 Push, Pop, Top등의 시간복잡도는 O(1) 이다
-
하지만, 탐색은 O(n) 이다
-> 데이터의 접근을 top에서부터 순차적으로 해야하기 때문에 탐색하려면 하나씩 pop( )해서 데이터를 확인해야한다
유니티에서 스택을 사용할만한 곳
나는 유니티를 사용하여 게임을 만들어야 하기에 스택을 어디서 사용하면 좋을 지 생각해보았다.
가장 마지막에 들어온 데이터가 가장 먼저 나가는 구조임을 생각해 보았을때, 뒤로가기 버튼에 적용시키면 좋을 거 같다
- 현재 게임 상태를 저장해두고, 상태를 변경하면 스택에 Push( )
- 뒤로가기를 했을때 Pop( )해서 이전에 저장된 상태를 꺼내기