개방주소법
개방주소법 (Open Addressing) : 해시 충돌이 발생하면 충돌이 일어난 버킷을 피해서 다른 버킷에 데이터를 저장하는 방식
분리체인법
분리체인법은 해시충돌이 발생하면, 체이닝 기법을 사용하는 것
(앞의 자료구조 해시테이블에서 사용하였다)
https://velog.io/@yangju058/자료구조-Hash-Table
선형탐색 (Linear Probing)
해시 함수가 두 개 이상의 동일한 인덱스로 들어 갈 경우, 충돌을 해결하기 위해 다른 인덱스를 찾아서 거기에 매핑하는 방식
- 체이닝 기법에서는 같은 해쉬인덱스값을 가져도 서로 연결하여 같은 버킷에 뒀지만, 선형탐색은 만약 버킷안에 이미 저장된 값이 있을 경우, 다른 빈자리 인덱스를 찾아서 값을 넣는다
-
아래의 사진에서 만약 내가 넣을 키값의 해쉬인덱스 값이 4면 4자리에 넣어야한다
-
하지만 이미 그 자리에 저장된 값이 있다
->index = (index + 1) % SIZE를 이용하여 인덱스 값을 갱신하여 빈자리를 찾는다
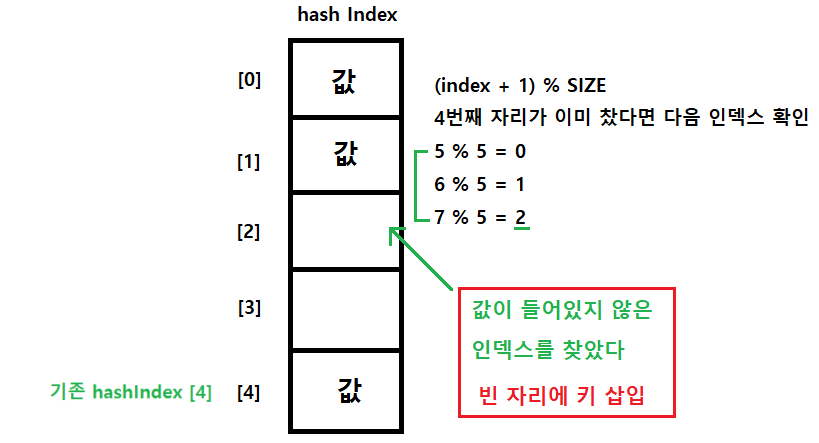
-
만약 인덱스를 다 탐색했는데도 값을 찾지 못하였다면
버킷안이 꽉 찼기 때문에 더 이상 값을 삽입할 수 없다
여기서 기존에 넣을려던 index곳과 현재 갱신해서 온 index자리가 같아지면 꽉찼다는 의미인데,
-> 정확히는 % SIZE 연산을 하기때문에 무조건 인덱스 범위가 SIZE내에서만 나와진다! (아래의 그림 확인)
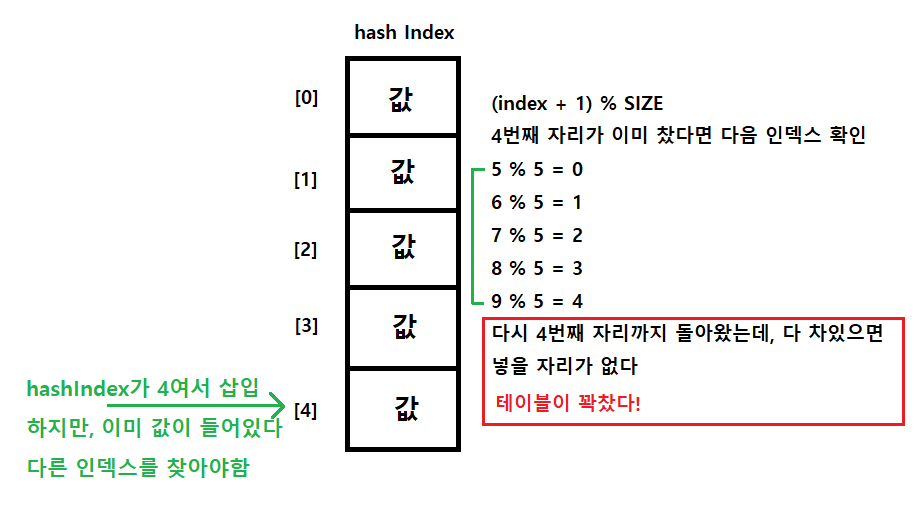
선형탐색 코드
해시인덱스에 값 삽입
// 값 삽입
void insert(int key) {
int index = hashFunction(key);
int originalIndex = index; // 충돌 발생 시 순차적으로 돌아야 하므로 원래 인덱스를 기억
while (table[index] != -1) { // 빈 공간이 아니면 선형 조사
index = (index + 1) % size;
if (index == originalIndex) {
cout << "Table is full!" << endl;
return; // 테이블이 꽉 찼을 경우
}
}
table[index] = key; // 빈 자리에 키 삽입
}해당 키 값 찾기
// 값 찾기
bool search(int key) {
int index = hashFunction(key);
int originalIndex = index;
while (table[index] != -1) {
if (table[index] == key) {
return true; // 값이 발견되면 true 반환
}
index = (index + 1) % size; // 선형 조사로 다음 인덱스 확인
if (index == originalIndex) {
break; // 원래 위치로 돌아오면 탐색 종료
}
}
return false; // 값을 찾지 못했을 경우 false 반환
}선형탐색 문제점
장점
- 체이닝 기법과 같이 추가적인 메모리를 사용하지 않기 때문에 메모리 사용이 적다
단점
-
버킷 안에 빈자리가 없을 경우, 값을 넣지 못한다
-
군집화 (클러스터링 clustering) 현상 발생
-> 계속해서 탐색하고 빈자리를 찾아서 들어가기 때문에,
여러 키가 서로 인접한 위치에 모여서 군집을 이루는 현상이 발생할 수 있다
-> 군집이 생길수록 빈 자리를 찾는 데 더 많은 시간이 걸린다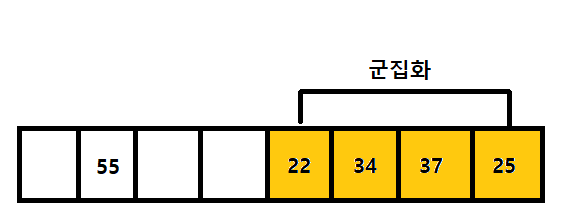
군집화가 발생하면, 탐색 능력과 삽입 능력이 저하되어 최악의 경우 O(N) 시간복잡도에 가까워진다
이 군집화의 해결책으로 리사이징, 이차해싱, 체이닝 기법을 사용한다
선형탐색 시간복잡도
-
삽입 : 키값이 주어지고 바로 해시인덱스 값에 넣을 수 있다면 O(1)
최악의 경우 O(N) -> 모든 버킷이 다 차있으면 모든 인덱스를 다 확인해야한다 -
삭제 : 평균적으로 O(1)이며, 최악의 경우는 O(N)
-
탐색 : 탐색은 값이 저장된 인덱스를 찾기 위해 선형 조사를 사용
-> 해당 인덱스에 내가 원하는 값이 있는지 찾기 때문에 해시 충돌이 적어서 인덱스의 이동이 적다면 O(1)
-> 최악의 경우는 O(N)
이차탐색 (Quadratic Probing)
선형탐색과 근본적으로 비슷한 방법이다
선형탐색의 문제점인 군집화를 해결하기 위한 방법이기도 하다
해시충돌이 발생할 때, 제곱수를 이용하여 충돌을 해결한다
-> 선형탐색에서는 한칸씩 순차적으로 탐색하지만, 이차탐색에서는 각 해시충돌 후 간격을 점차적으로 증가시켜 충돌을 분산시킨다
이차탐색 원리
기존 선형탐색에서는 인덱스를 찾아가는 과정이
index = (index + 1) % SIZE 였다면
이차탐색은 선형적으로 증가시키는 것이 아닌 제곱수로 증가된다
index = (index + n²) % SIZE
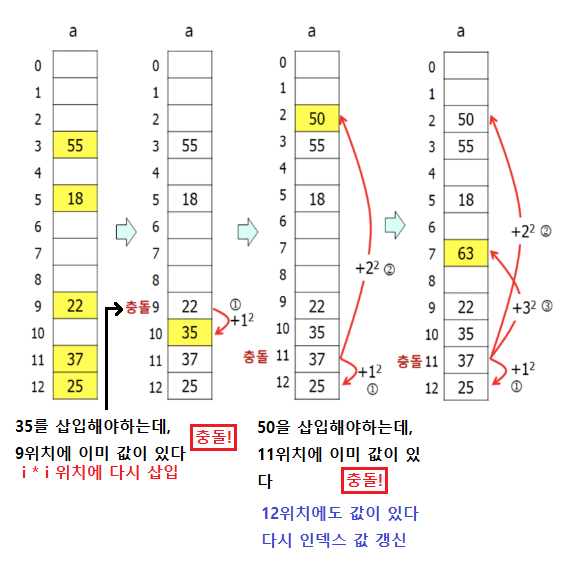
출처: https://m.blog.naver.com/beaqon/221300392786?recommendTrackingCode=2
이차탐색 코드
해시인덱스에 값 삽입
// 값 삽입
void insert(int key) {
int index = hashFunction(key);
int i = 1; // 첫 번째 충돌부터 시작
// 충돌이 발생하면 이차 탐사를 통해 빈 자리를 찾음
while (table[index] != -1) {
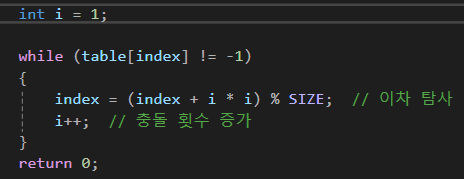
index = (index + i * i) % size; // 이차 탐사
i++; // 충돌 횟수 증가
}
table[index] = key; // 빈 자리에 키 삽입
}이 부분이 이차탐색의 핵심이다
(index + i * i) 부분은 현재 인덱스에서 i번째 충돌에 대한 제곱수만큼 이동한 새로운 인덱스를 계산하는 부분이다
- 첫 시작이
i = 1부터인데, 만약 버킷의 값이 이미 들어있다면 새로운 인덱스 위치에 값을 삽입해야한다
해당 키 값 찾기 (탐색)
// 값 찾기
bool search(int key) {
int index = hashFunction(key);
int i = 1; // 첫 번째 충돌부터 시작
// 선형 탐사처럼 충돌이 발생하면 이차 탐사를 통해 값 찾음
while (table[index] != -1) {
if (table[index] == key) {
return true; // 값이 발견되면 true 반환
}
index = (index + i * i) % size; // 이차 탐사
i++; // 충돌 횟수 증가
}
return false; // 값을 찾지 못했을 경우 false 반환
}이차탐색 문제점
장점
- 군집화를 방지한다
-> 선형탐색에서 발생하던 군집화가 이차탐색에서는 분산되기 때문에 탐색효율이 향상된다
단점
-
선형 탐색보다 간격이 커지기 때문에, 만약 충돌이 많을 경우 탐색이 오래걸린다
-
모든 버킷이 꽉차면 값을 넣을 수 없다 (리사이징 필요)
-
선형탐색에서 발생하는 1차 군집화를 해결하긴 하지만, 같은 해시값을 갖는 키들은 똑같은 방식으로 빈 원소를 찾아내기 때문에 결국 또 다른 군집을 발생시킨다
-> 2차 군집화
이차탐색 시간복잡도
-
삽입: 평균적으로 충돌이 적다면 O(1)
-> 최악의 경우: 계속 충돌하여 자리가 없을때까지 탐색하면 O(N) -
삭제: 삭제 후에 이차탐색으로 계속 이동해야하기 때문에 O(N)
-> 보통은 군집화가 발생하더라도 O(1) 시간에 삭제할 수 있는 경우가 많다 -
탐색: 일반적인 탐색 시간복잡도는 O(1)이다
-> 충돌이 적고, 군집화가 최소화라면 상수시간에 탐색가능
-> 충돌이 많고, 군집화가 심한 경우 순차적으로 모든 버킷을 탐색해야하기 때문에 O(N)
-> 충돌이 계속발생하면 인덱스를 이동하고, 거기서 또 충돌이 발생하여 이동하고가 반복된다
리사이징 (Resizing)
리사이징 사용 코드
#include <iostream>
#include <vector>
using namespace std;
class HashTable {
private:
vector<int> table;
int size;
int currentSize; // 현재 테이블에 삽입된 원소의 개수
public:
HashTable(int size) {
this->size = size;
currentSize = 0;
table.resize(size, -1); // -1로 초기화 (빈 공간을 나타냄)
}
// 해시 함수
int hashFunction(int key) {
return key % size;
}
// 리사이징: 테이블 크기 두 배로 확장
void resize() {
int newSize = size * 2;
vector<int> newTable(newSize, -1);
// 기존 테이블의 항목을 새로운 테이블로 재배치
for (int i = 0; i < size; i++) {
if (table[i] != -1) {
int key = table[i];
int index = key % newSize;
int j = 1;
// 충돌 발생 시 이차 탐사를 사용해 재배치
while (newTable[index] != -1) {
index = (index + j * j) % newSize;
j++;
}
newTable[index] = key;
}
}
table = newTable;
size = newSize; // 테이블 크기 업데이트
}
// 삽입
void insert(int key) {
if (currentSize >= size / 2) {
resize(); // 테이블이 절반 이상 차면 리사이징
}
int index = hashFunction(key);
int i = 1;
// 충돌이 발생하면 이차 탐사를 사용해 빈 슬롯을 찾음
while (table[index] != -1) {
index = (index + i * i) % size;
i++;
}
table[index] = key;
currentSize++;
}
// 값 찾기
bool search(int key) {
int index = hashFunction(key);
int i = 1;
while (table[index] != -1) {
if (table[index] == key) {
return true;
}
index = (index + i * i) % size;
i++;
}
return false;
}
// 테이블 출력
void display() {
for (int i = 0; i < size; i++) {
cout << i << ": " << table[i] << endl;
}
}
};
int main() {
HashTable ht(5); // 테이블 크기 5
ht.insert(12);
ht.insert(22);
ht.insert(32); // 테이블 크기 5에서 삽입
ht.insert(42); // 리사이징 후 테이블 크기 증가
ht.insert(52); // 리사이징 후 삽입
ht.display(); // 테이블 내용 출력
return 0;
}

