[프로그래머스] 둘만의 암호

이얀조·2023년 3월 20일

🎀프로그래머스

목록 보기

7/21

🛴 문제 설명

두 문자열 s와 skip, 그리고 자연수 index가 주어질 때, 다음 규칙에 따라 문자열을 만들려 합니다. 
암호의 규칙은 다음과 같습니다.
문자열 s의 각 알파벳을 index만큼 뒤의 알파벳으로 바꿔줍니다.
index만큼의 뒤의 알파벳이 z를 넘어갈 경우 다시 a로 돌아갑니다.
skip에 있는 알파벳은 제외하고 건너뜁니다.
예를 들어 s = "aukks", skip = "wbqd", index = 5일 때, a에서 5만큼 뒤에 있는 알파벳은 f지만 
[b, c, d, e, f]에서 'b'와 'd'는 skip에 포함되므로 세지 않습니다. 
따라서 'b', 'd'를 제외하고 'a'에서 5만큼 뒤에 있는 알파벳은 [c, e, f, g, h] 순서에 의해 'h'가 됩니다. 
나머지 "ukks" 또한 위 규칙대로 바꾸면 "appy"가 되며 결과는 "happy"가 됩니다.
두 문자열 s와 skip, 그리고 자연수 index가 매개변수로 주어질 때 위 규칙대로 s를 변환한 결과를 return하도록 solution 함수를 완성해주세요.

💦 제한사항

5 ≤ s의 길이 ≤ 50
1 ≤ skip의 길이 ≤ 10
s와 skip은 알파벳 소문자로만 이루어져 있습니다.
- skip에 포함되는 알파벳은 s에 포함되지 않습니다.
1 ≤ index ≤ 20

👨🏻‍🦱 풀이

해당 문제를 해결하기 위하여 두가지 방법을 고안했다.

알파벳 전체 vector(혹은 배열) 에서 skip 값을 erase
skip 값을 계속 각 s배열을 탐색할 때 마다 같이 탐색

결과적으로 두 방법은 적합하지 않았다고 생각한다.

먼저 erase 하게 될 경우 for문 탐색시 index로 접근하기 때문에 제대로 탐색이 되지 않는다.
두번째로는 skip 배열 을 탐색하는 것은 보다 로직이 보다 복잡해 진다고 느꼈다.

따라서

알파벳 전체 vector 에서 skip 배열에 해당하는 값은 "1"로 지정하여 vector를 탐색하자

즉 다음과 같다.
현재 s배열과 skip이 반영된 alphaNums 라는 전체 알파벳 배열이 있다.

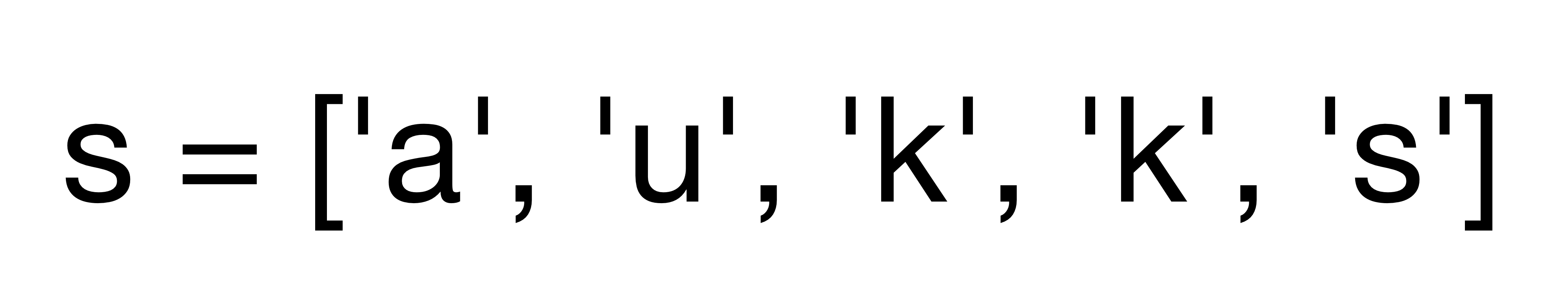
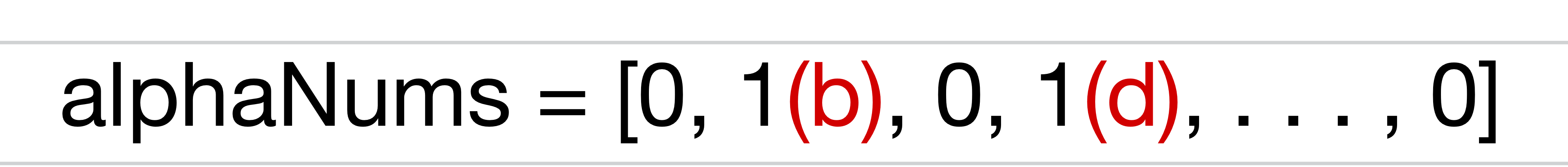
alphaNums를 보면 skip에 해당하는 b, d 에 1로 할당 되어있음을 알 수 있다.

이후 s 배열의 각 값을 탐색하면서 while 문을 이용하여 index 만큼 이동하는 지를 체크한다.

예시로 a, u 두가지를 들어보면

a 는 idx가 0으로 시작한다.
이를 while 문을 통해 idx가 index와 같은 값이 될 때 까지 탐색하도록 한다.

이때 중간에 b, d 의 경우 skip 배열의 값이므로 idx를 증가시키지 않는다.
그렇게 되면 index 즉 5의 값이 되는 idx의 순간은 h가 되는 것이다.

동일하게 u를 본다면 다음과 같다.

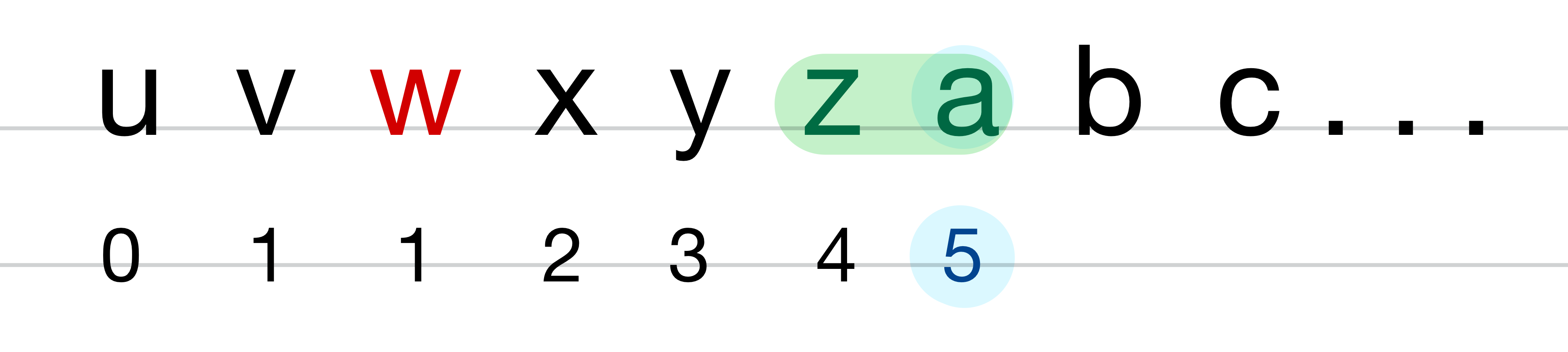
다만 여기서 주의할 점은 z 인데, z의 아스키 코드 값은 "122" 이며 z에서 그대로 다음 값으로 넘어가면 "123" 으로 값을 넘어가게 된다.
따라서 z → a로 넘어가게 되는 경우를 처리해 주어야 한다.

하지만 이럼에도 간과했던 부분이 있었는데, 질문하기 를 통해 반례를 발견하였다.

반례 보기 > s = "zzzzz"
skip = "abcdefghijklmnopqrstuvwxy"
index = 6

result = "zzzzz"

🎨 코드

#include <string>
#include <vector>
#include <iostream>
using namespace std;

string solution(string s, string skip, int index) {
    string answer = "";
    vector<int> alphaNums(26, 0);

    // alphaNums에 skip 값들은 1로 바꿈
    for (int i = 0; i < skip.length(); i++) {
        alphaNums[skip[i] - 97] = 1;
    }
    
    for (int j = 0; j < s.length(); j++) {
        // s 값
        int sNum = s[j];
        int tmpIdx = 0;
        
        while(tmpIdx < index) {
            if (++sNum > 122) sNum -= 26;
            if (alphaNums[sNum - 97] == 0) tmpIdx += 1;
        }
        answer += (char)sNum;
    }

    return answer;
}

🛶 어려웠던 점

1. 깔끔하지 못한 로직
→ 나머지(mod) 를 이용하여 처리를 했다면 더움 깔끔했을 것 같은데 계속 상수(아스키 코드 값인 97 or 알파벳 갯수인 26) 를 사용하여 코드적으로는 좋지 않았던 것 같다.
2. index 값을 제대로 탐색하지 않음
→ index 가 5라면 5만큼 건너 뛴 후에 그 사이에 skip이 있다면 마지막에 더하는 방식으로 진행하고자 하였다.
→ 하지만 해당 방식으로 진행을 하게 되면 반례가 통과되지 않는다.
→ 따라서 반례를 간과한 경우 이다.

이얀조

이얀조다!

이전 포스트

[프로그래머스] 두 큐 합 같게 만들기

다음 포스트

[프로그래머스] 둘만의 암호