[알고리즘] 그리디 풀이 - 2

Kevin·2025년 3월 1일
백준 10162백준 10610백준 1202백준 1439백준 1946

Algorithm

목록 보기
3/10
post-thumbnail

1️⃣ 전자레인지

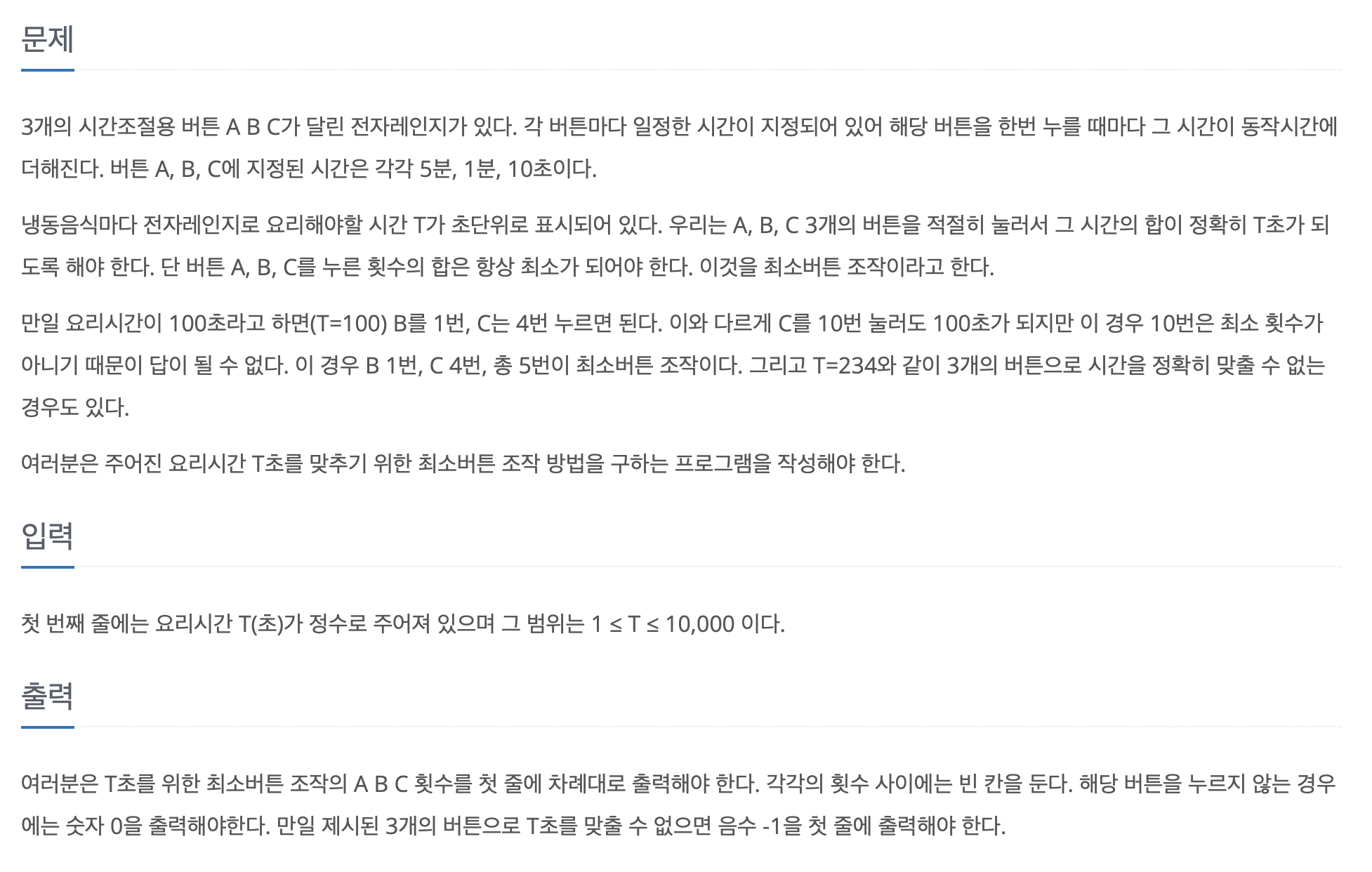
정답

import java.io.*;

public class Main {

    public void solution() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(br.readLine());

        int aCnt = 0;
        int bCnt = 0;
        int cCnt = 0;

        int a = 5 * 60;
        int b = 1 * 60;
        int c = 10;

        if (n % 10 != 0) {
            bw.write(-1 + "\n");
        } else {
            if (a <= n) {
                aCnt = n / a;
                n %= a;
            }

            if (b <= n) {
                bCnt = n / b;
                n %= b;
            }

            if (c <= n) {
                cCnt = n / c;
                n %= c;
            }

            bw.write(aCnt + " " + bCnt + " " + cCnt + "\n");
        }

        br.close();
        bw.close();
    }

    public static void main(String[] args) throws IOException {
        new Main().solution();
    }
}

해당 문제를 풀 때 핵심은 가지고 있는 숫자(300, 60, 10 (초)) 중 가장 큰 단위인 300이 10의 배수라는 것을 토대로 작은 단위의 숫자들을 종합해서 다른 해가 나올 수 없다는 것이다.

그렇기에 가장 큰 단위인 C로 가장 많이 나누는게 최소 횟수를 구하는 답이다.

배운 점

  • 해당 문제는 거스름돈 문제와 같이 그리디 알고리즘으로 해결할 수 있는 이유는 가지고 있는 숫자 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 숫자들을 종합해 다른 해가 나올 수 없기 때문이라는 것을 깨달았다.

https://www.acmicpc.net/problem/10162


2️⃣ 뒤집기

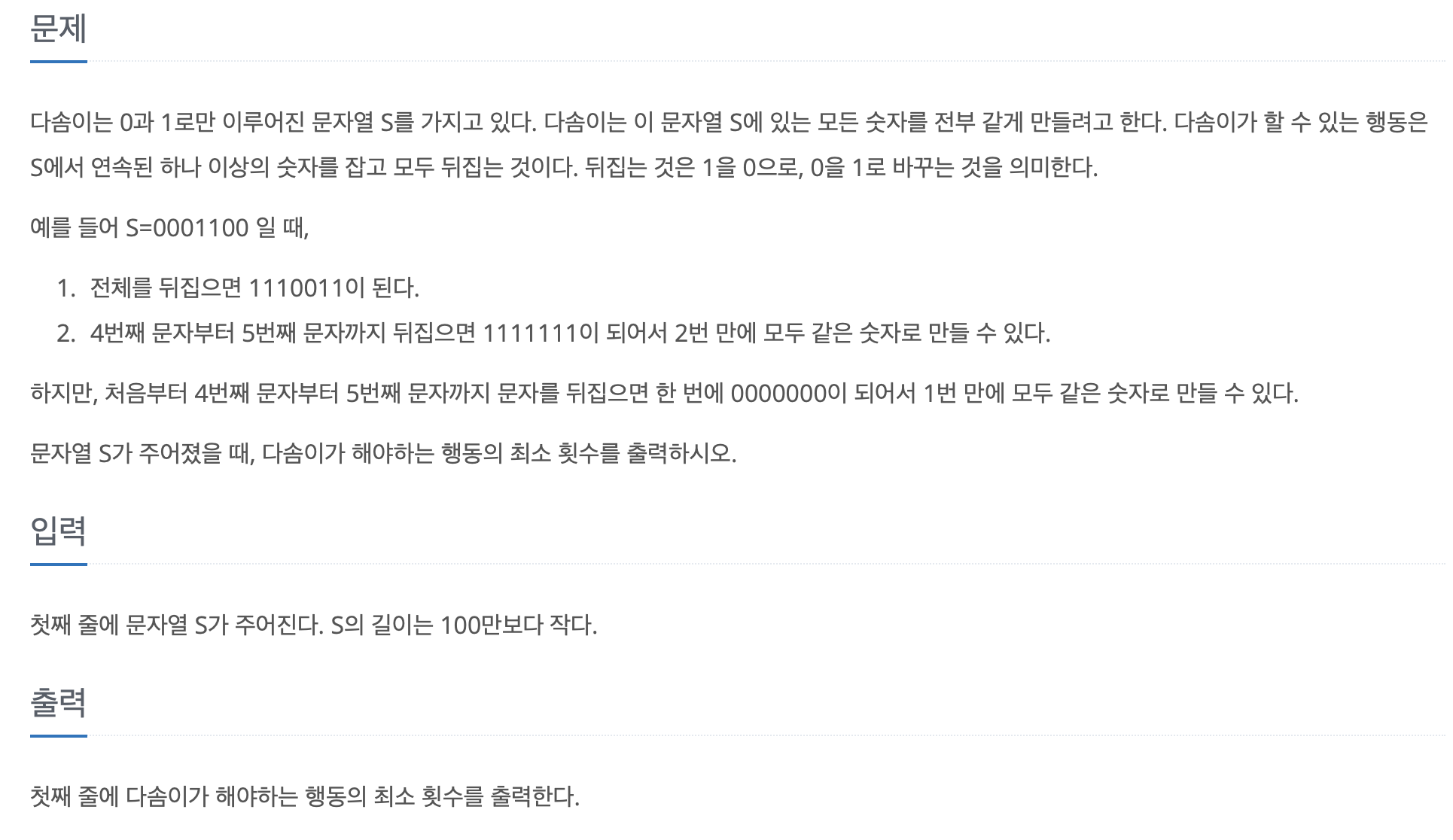
정답

import java.io.*;
import java.util.Objects;
import java.util.StringTokenizer;

public class Main {

    public void solution() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        String[] strArr = br.readLine().split("");

        int oneAns = 0;
        int zeroAns = 0;
        int idx = 1;

        String num = strArr[0];

        while (true) {

            if (idx == strArr.length) {
                break;
            }

            if (!Objects.equals(num, strArr[idx])) { // 만약 숫자가 연속 되었다면 해당 그룹의 카운트를 1 더 해야 함.
                if (Objects.equals(num, "1")) {
                    oneAns += 1;

                } else {
                    zeroAns += 1;
                }

                num = strArr[idx];
            }

            idx++;
        }

        if (oneAns + zeroAns == 1) {
            bw.write(1 + "\n");
        } else if (Objects.equals(strArr[0], "1") && oneAns == zeroAns + 1) {
            bw.write(oneAns + "\n");
        } else if ("0".equals(strArr[0]) && oneAns + 1 == zeroAns) {
            bw.write(zeroAns + "\n");
        } else {
            bw.write(Math.min(oneAns, zeroAns) + "\n");
        }

        br.close();
        bw.close();
    }

    public static void main(String[] args) throws IOException {
        new Main().solution();
    }
}

로직은 간단하다.

각 그룹(00이나 11)등의 횟수들을 각각 구해주고, 둘 중 더 작은 값을 사용 하면 된다.

그러나 답을 처리하는 과정에 로직의 불안정함(=맨 끝 인덱스의 숫자에 대해서는 그룹화를 짓지 않은 것 등)을 마지막 답을 나누는 분기에서 직접 작성했다.

이러한 방법이 답의 경우의 수가 현저히 적은 난이도가 쉬운 문제였기에 다행이지, 경우의 수가 많은 문제였다면 답에서 분기를 나누는 방법은 사용 하지 못했을 것 같다.

답을 맞췄다만 무언가 찝찝함이 남는다.

다른 사람 풀이

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    private void solution() throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String s = br.readLine();
        StringTokenizer st1 = new StringTokenizer(s, "0");
        StringTokenizer st0 = new StringTokenizer(s, "1");
        System.out.println(Math.min(st1.countTokens(), st0.countTokens()));
    }

    public static void main(String[] args) throws Exception {
        new Main().solution();
    }
}

출처 : https://nahwasa.com/entry/%EB%B0%B1%EC%A4%80-1439-%EC%9E%90%EB%B0%94-%EB%92%A4%EC%A7%91%EA%B8%B0-BOJ-1439-JAVA

  1. 0과 1을 구분자로 하여서 그룹들을 각기 나눠서 넣는다.
    1. ex) 0001000, 0001000
  2. 이 때 해당 그룹의 개수를 countTokens()을 통해 반환 받는다.

배운 점

  • 이런 문자열을 기반으로 하는 문제를 JAVA로 풀 때 StringTokenizer를 사용하느냐 안하느냐는 하늘과 땅 차이구나.
  • .split("") 을 통해서 문자열을 각각 문자열 배열 원소로 만들어 줄 수 있구나.

https://www.acmicpc.net/problem/1439

https://crazykim2.tistory.com/552


3️⃣ 신입 사원

틀린 답(시간 초과)

import java.io.*;
import java.util.*;

public class Main {

    public void solution() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());

        for (int i=0; i < n; i++) {

            st = new StringTokenizer(br.readLine());

            int cnt = Integer.parseInt(st.nextToken());
            int [][] arr = new int [cnt][2];

            int ans = 0;

            for (int j = 0; j < cnt; j++) {
                st = new StringTokenizer(br.readLine(), " ");
                arr[j][0] = Integer.parseInt(st.nextToken());
                arr[j][1] = Integer.parseInt(st.nextToken());
            }

            Arrays.sort(arr, (o1, o2) -> {

                if(o1[0] == o2[0]) {
                    return o1[1] - o2[1];
                }

                return o1[0] - o2[0];
            });

            Set<Integer> set = new HashSet<>(); // 만약 1보다 큰 값 있으면 인덱스 set에 추가

            for (int l = 0; l < arr.length; l++) {

                int tmpNum = arr[l][1];

                for (int q = l; q < arr.length; q++) {
                    if (arr[q][1] > tmpNum) {
                        set.add(q);
                    }
                }
            }

            bw.write(arr.length - set.size() + "\n");

        }

        br.close();
        bw.close();
    }

    public static void main(String[] args) throws IOException {
        new Main().solution();
    }
}

첫번째 인덱스를 기준으로 배열을 오름차순 정렬 후

즉 오름차순 정렬 된 (1, 4), (2, 5), (3, 6), (4, 2)인 2차원 배열이 있을 때

가장 첫번째 인덱스인 (1, 4)의 4보다 더 큰 값은 서류 심사와 면접 결과 모두 떨어지는 것이라 가정 할 수 있다.

정답

import java.io.*;
import java.util.*;

public class Main {

    public void solution() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int t = Integer.parseInt(br.readLine().trim()); // 테스트 케이스 수

        for (int i = 0; i < t; i++) {
            int cnt = Integer.parseInt(br.readLine().trim());
            int[][] arr = new int[cnt][2];

            // 후보들의 등수 입력
            for (int j = 0; j < cnt; j++) {
                StringTokenizer st = new StringTokenizer(br.readLine());
                arr[j][0] = Integer.parseInt(st.nextToken()); // 서류 등수
                arr[j][1] = Integer.parseInt(st.nextToken()); // 면접 등수           }

            // 서류 등수를 기준으로 오름차순 정렬 (서류 등수가 같으면 면접 등수 기준 오름차순)
            Arrays.sort(arr, (o1, o2) -> {
                if (o1[0] == o2[0]) {
                    return o1[1] - o2[1];
                }
                return o1[0] - o2[0];
            });

            // 한 번의 순회로 후보 선정
            int count = 0;
            int bestInterview = Integer.MAX_VALUE;
            for (int j = 0; j < cnt; j++) {
                // 현재 후보의 면접 등수가 지금까지의 최소 등수보다 낮다면, 합격 후보로 선정
                if (arr[j][1] < bestInterview) {
                    count++;
                    bestInterview = arr[j][1];
                }
            }

            bw.write(count + "\n");
        }

        bw.flush();
        br.close();
        bw.close();
    }

    public static void main(String[] args) throws IOException {
        new Main().solution();
    }
}

이전 코드에서 아래 경우에 최악의 경우 O(n2)의 시간 복잡도를 가지게 된다.

for (int l = 0; l < arr.length; l++) {
    int tmpNum = arr[l][1];
    for (int q = l; q < arr.length; q++) { 
        if (arr[q][1] > tmpNum) {
            set.add(q);
        }
    }
}

그리하여 해당 부분 자체의 알고리즘을 변경 하였다.

이중 반복문을 사용하지 않고, 만약 현재 후보의 면접 등수가 기존의 등수보다 낮다면 합격자 등수로 포함 시켜주면 된다.

이는 O(n1)의 시간 복잡도만 갖게 되어 이전에 가진 시간 초과 문제를 해결 할 수 있다.

배운 점

  • 주어진 테스트 케이스들에 대한 답이 어떻게 도출 되었는지를 고민 하고, 이를 어떻게 알고리즘화 할 것인지 설계 및 수도 코드를 작성하는 것이 큰 도움이 된다.
  • 지금까지 백준을 풀면서 시간 복잡도에 대해서 크게 고민 해본적이 없었다. 그러나 이번에 시간 초과를 겪게 되면서, 시간 복잡도 특히 이중 반복문등을 최대한 피해야겠다는 생각을 가지게 되었다.
  • 만약 배열의 첫번째 인덱스부터 끝 인덱스까지 지속적으로 비교 해야 할 경우가 있다면, 이중 반복문을 돌리지 말고 최소 또는 최대값 변수를 선언해두고 이를 통해 비교 하자.

https://www.acmicpc.net/problem/1946


4️⃣ 30

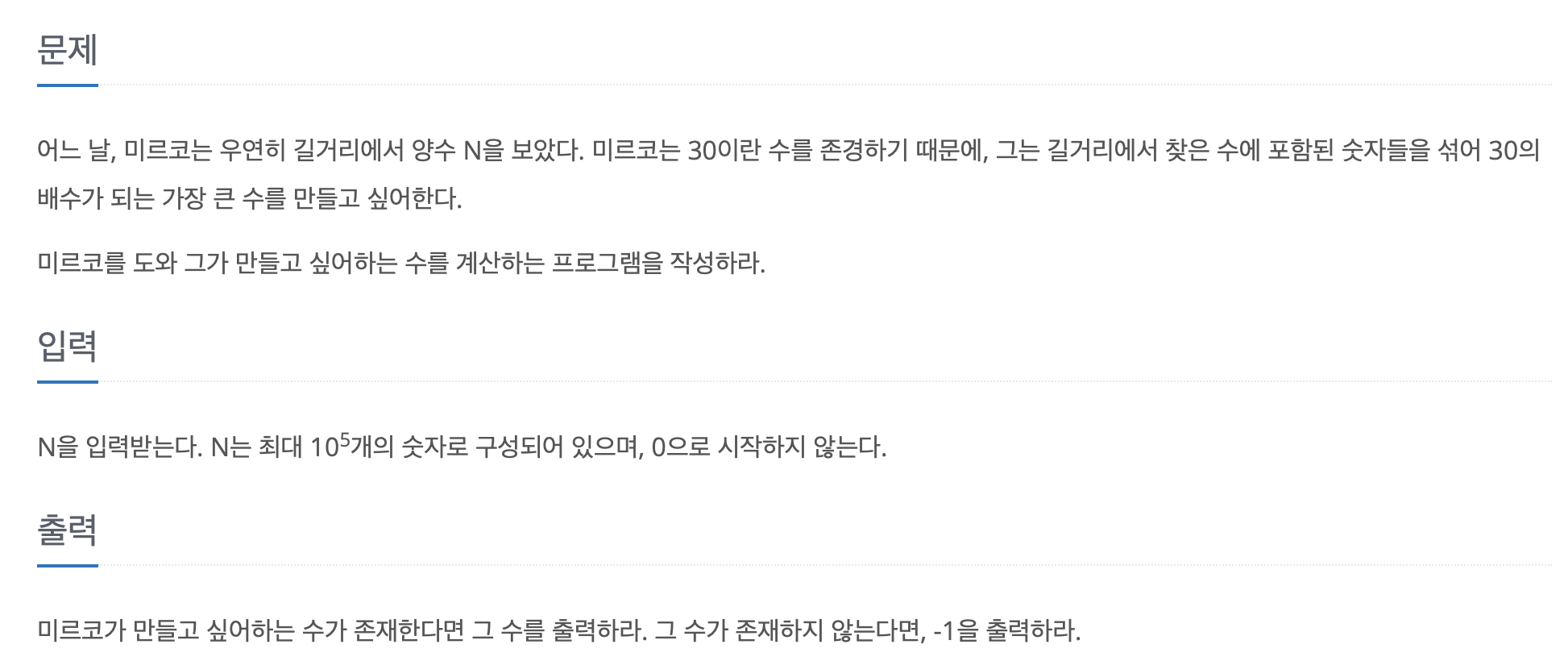
정답

import java.io.*;
import java.util.*;

public class Main {

    public void solution() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer subSt = new StringTokenizer(br.readLine(), "");

        String[] numArr = subSt.nextToken().split("");

        Arrays.sort(numArr, Collections.reverseOrder());

        List<String> ansArr = Arrays.asList(numArr);

        int sum = 0;
        String ans = "";

        for (String num : ansArr) {
            sum += Integer.parseInt(num);
            ans += num;
        }

        if (ansArr.contains("0") && sum % 3 == 0) {
            bw.write(ans + "\n");
        } else {
            bw.write(-1 + "\n");
        }

        br.close();
        bw.close();
    }

    public static void main(String[] args) throws IOException {
        new Main().solution();
    }
}

맨 처음 모든 자리의 수를 바꿔가면서, 모든 가능한 경우의 수들을 만들어 이를 해결 하고자 했다.

그러나 해당 문제에서는 아래와 같은 규칙이 있었기에, 다른 방식으로 풀이 하였다.

  1. 숫자 중 0이 존재 해야한다.
    1. 그 이유로는 30의 배수는 반드시 0으로 끝나기 때문이다.
  2. 배수판정법에 의거해서 각 자리의 수를 더했을 때의 값이 3의 배수이어야 한다.
    • 3의 배수 → 각 자리수를 더한 값이 3의 배수
    • 9의 배수 → 각 자리수를 더한 값이 9의 배수
    • 2의 배수 → 끝자리가 0, 2, 4, 6, 8
    • 5의 배수 → 끝자리가 0 또는 5
    • 10의 배수 → 끝자리가 0
    • 4의 배수 → 끝 두 자리가 4의 배수
    • 8의 배수 → 끝 세 자리가 8의 배수
    • 6의 배수 → 2의 배수 & 3의 배수 조건을 동시에 만족해야 함

배운 점

  • 맨 처음 구상한 풀이 방법은 순열 알고리즘에 가까우며, 해당 알고리즘 또한 추후에 공부를 해야겠다. https://velog.io/@soyeon207/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%88%9C%EC%97%B4-yaxs0hh7
  • String 형의 배열안의 숫자로 된 문자도 내림차순을 동일하게 적용 받는다는 것을 알았다.
  • 숫자의 규칙을 만드는 것이 얼마나 중요한지를 알았다.
  • 숫자로 변환하여 풀 때 입력이나 출력에 주어진 조건을 초과하지 않는지를 살펴봐야겠다.

https://www.acmicpc.net/problem/10610


5️⃣ 보석 도둑

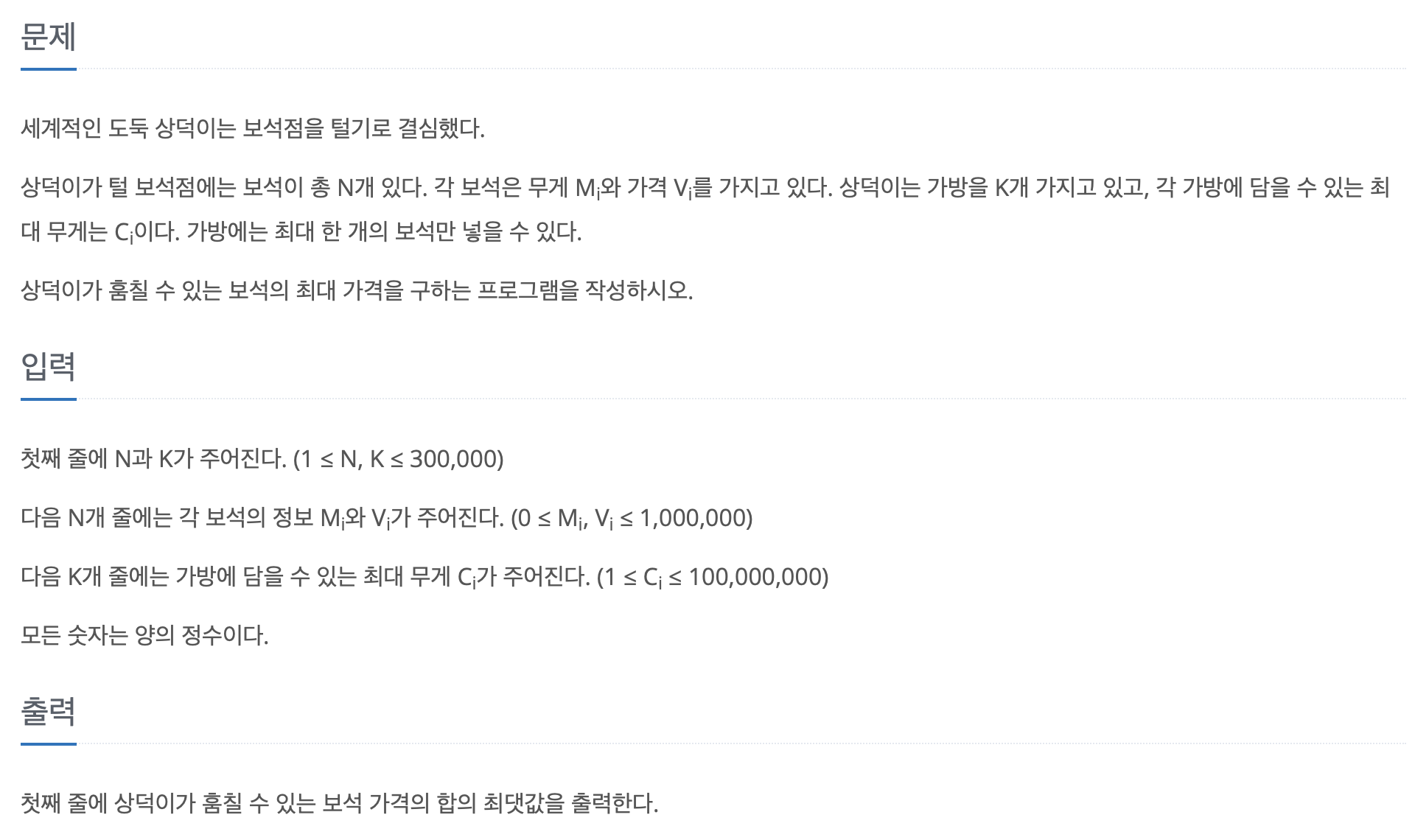
틀린 답

import java.io.*;
import java.util.*;

public class Main {

    public void solution() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        long ans = 0;

        int[][] nArr = new int[n][2];

        for (int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            nArr[i][0] = Integer.parseInt(st.nextToken());
            nArr[i][1] = Integer.parseInt(st.nextToken());
        }

        int[] bArr = new int[k];

        for (int i = 0; i < k; i++) {
            bArr[i] = Integer.parseInt(br.readLine());
        }

        Arrays.sort(nArr, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o2[1] - o1[1];
            }
        });

        Arrays.sort(bArr);

        int bIdx = 0; // 가방 용량 인덱스

        for (int i = 0; i < n; i++) {
            if (bIdx == bArr.length) {
                break;
            }

            if (nArr[i][0] <= bArr[bIdx]) { // 가방에 담는다.
                ans += nArr[i][1];
                bIdx++;
            }
        }

        bw.write(ans+ "\n");

        br.close();
        bw.close();
    }

    public static void main(String[] args) throws IOException {
        new Main().solution();
    }
}

핵심은 “가장 가치 있는 비용을 가장 용량이 가장 작은 가방에 넣을 수 있다면 넣는다”이다.

이를 이루기 위해서 보석은 내림차순으로 정렬하고, 가방은 가장 작은 가방부터 오름차순으로 정렬을 해야한다.

이를 통해 코드를 작성 하였으나 아래의 반례를 통과 하지 못했다.

4 4
1 100
2 200
13 300
10 500
10
10
10
14

해당 반례를 예로 들어보겠다.

보석은 가격 기준으로 내림차순하면 다음과 같다.

10 500
13 300
2 200
1 100

가방을 무게로 오름차순 하면 아래와 같다.

10
10
10
14
  1. 이 때 10kg의 보석은 맨 처음 10kg 용량의 가방에 들어갈 것이다.
  2. 13kg의 보석은 이 때 14kg으로 찾아가는게 맞으나 위 로직에서는 건너뛰고 2와 1 kg 보석을 가방에 담는 로직이 진행된다.

정답

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        int n = Integer.parseInt(st.nextToken()); // 보석 개수
        int k = Integer.parseInt(st.nextToken()); // 가방 개수

        int[][] jewels = new int[n][2]; // 보석 정보 (무게, 가격)
        for (int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            jewels[i][0] = Integer.parseInt(st.nextToken());
            jewels[i][1] = Integer.parseInt(st.nextToken());
        }

        int[] bags = new int[k];

        for (int i = 0; i < k; i++) {
            bags[i] = Integer.parseInt(br.readLine());
        }

        Arrays.sort(jewels, Comparator.comparingInt(o -> o[0]));

        Arrays.sort(bags);

        PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());

        int j = 0; // 보석 인덱스 
        long ans = 0; // 결과 값 (최대 가격 합)

        // 작은 가방부터 탐색
        for (int bag : bags) {
            // 현재 가방(`bag`)이 담을 수 있는 보석들을 `pq`에 추가
            while (j < n && jewels[j][0] <= bag) {
                pq.offer(jewels[j][1]); // 가격만 `pq`에 추가
                j++;
            }
            // `pq`에서 가장 비싼 보석을 선택하여 추가
            if (!pq.isEmpty()) {
                ans += pq.poll();
            }
        }

        bw.write(ans + "\n");

        br.close();
        bw.close();
    }
}

위 코드에서의 가장 큰 패착인 보석을 담을 수 있는 가방을 순환하여 찾아야 된다는 점을 보완하면 된다.

이를 우선순위 큐를 통해 해결 하였다.

while문에서 해당 가방이 담을 수 있는 보석들을 우선순위 큐에 모두 담아둔다.

그리고 이 중 가장 가치 있는 보석만 선택하여 정답에 추가한다.

배운 점

  • 우선순위 큐를 입력 값을 처음에 받는게 아니라 순환을 위해 값들을 담아두는 자료구조로 사용할 수도 있구나.
  • 주어진 시간이 짧다 해서 반복문의 사용을 너무 안하려고 했다.
    • 반복문을 사용하되, 범위를 명확히 하자.
  • 내가 풀고자 하는 방식을 너무 알고리즘적으로 푸려고 하는 것 같다.
    • 과감하게 시간 제한을 생각하여 자료구조로 풀 수 없을까? 라고 생각 해보자.

https://www.acmicpc.net/problem/1202

profile
Kevin
Hello, World! \n
이전 포스트

[알고리즘] 그리디 풀이 - 1

다음 포스트

[알고리즘] 그리디 풀이 - 3

0개의 댓글