
1️⃣ 기타줄 - 1049
문제

틀린 답
import java.io.*;
import java.util.*;
public class Main {
public void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int[] packageCosts = new int[m];
int[] divCosts = new int[m];
for (int i = 0; i < m; i ++) {
st = new StringTokenizer(br.readLine(), " ");
packageCosts[i] = Integer.parseInt(st.nextToken());
divCosts[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(packageCosts);
Arrays.sort(divCosts);
int line = n;
int packageCost = packageCosts[0];
int divCost = divCosts[0];
int ans = 0;
if (divCost * line <= packageCost) { // 처음부터 만약 낱개로 사는게 더 싸다면 낱개로 산다.
ans += divCost * line;
line = 0;
} else if (line > 6) { // 패키지로 구매
ans += packageCost * (line / 6);
line %= 6;
} else { // 패키지로 구매 하되 한번만 구매
line = 0;
ans += packageCost;
}
if (line > 0) { // 남았다면 낱개로 구매
ans += divCost * line;
}
bw.write(Math.min(ans, ((int) Math.ceil((double) n / 6)) * packageCost) + "\n"); // 패키지로만 구매한 것과 비교
bw.flush();
br.close();
bw.close();
}
public static void main(String[] args) throws IOException {
new Main().solution();
}
}
이 문제는 3가지 경우로 나뉘어진다.
- 낱개로만 살 때
- 패키지와 낱개로 살 때
- 패키지로만 살 때
이 셋의 최소값을 계산 하면 된다.
접근 자체가 매우 쉬운 문제였고, 예시 테케와 게시판 테케 모두 정답을 받았다.
그러나 50%에서 틀렸고, 반례를 더욱 찾아보던 중 아래 반례를 찾았다.
16 1
7 1
정답 : 16
내 답 : 18내 첫 코드의 문제점은 각 경우의 최소값을 비교 하는 것이 아니라 분기 처리를 통해서 해당 계산의 답이 최적의 해라는 것을 전제로 계산을 했다는 것이다.
정답
import java.io.*;
import java.util.*;
public class Main {
public void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int[] packageCosts = new int[m];
int[] divCosts = new int[m];
for (int i = 0; i < m; i ++) {
st = new StringTokenizer(br.readLine(), " ");
packageCosts[i] = Integer.parseInt(st.nextToken());
divCosts[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(packageCosts);
Arrays.sort(divCosts);
int packageCost = packageCosts[0];
int divCost = divCosts[0];
int cost1 = ((int) Math.ceil(n / 6.0)) * packageCost; // 1. 패키지만 구매했을 때
int cost2 = n * divCost; // 2. 낱개로만 구매했을 때
int cost3 = (n / 6) * packageCost + (n % 6) * divCost; // 3. 패키지 + 낱개 조합 (패키지는 몫만큼 사고, 나머지는 낱개로)
int minAns = Math.min(cost1, cost2);
bw.write(Math.min(minAns, cost3) + "\n"); // 패키지로만 구매한 것과 비교
bw.flush();
br.close();
bw.close();
}
public static void main(String[] args) throws IOException {
new Main().solution();
}
}
다른 이들의 코드 풀이 방식
https://tussle.tistory.com/917
- 전역 변수로 필요한 변수들을 선언
배운 점
- 그리디 문제에서는 각 경우에 대한 최소값을 비교 해야 하는 경우가 많다.
- 단순히 최적의 해라고 계산 하지 말자.
2️⃣ 거스름돈 - 14916
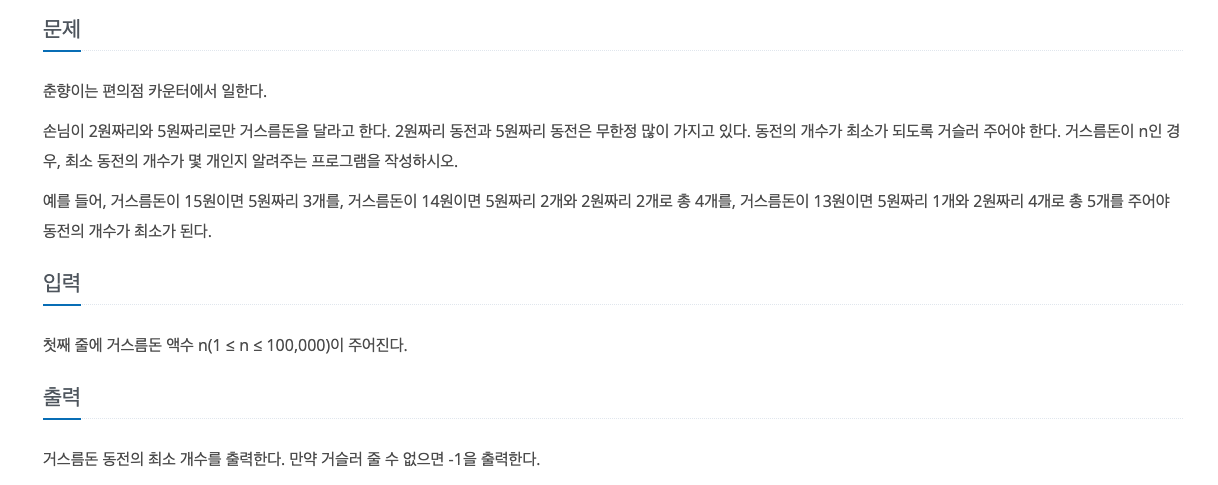
문제
정답
import java.io.*;
public class Main {
public void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
int ans = 0;
int minAns = Integer.MAX_VALUE;
while (true) {
if (n % 5 == 0) { // 5로 나누어 떨어질 때
ans += n / 5;
bw.write(ans + "\n");
break;
}
if (n % 2 == 0) { // 2로 나누어 떨어질 때
minAns = Math.min(minAns, n / 2);
}
if (n < 5 && n % 2 == 0) { // 5보다 작고 2로 나누어 떨어질 때
bw.write(ans + minAns + "\n");
break;
}
n -= 5; // 매 턴마다 5씩 제 해준다.
ans ++;
if (n < 0) { // 음수일 때
bw.write(-1 + "\n");
break;
}
if (n < 5 && n % 2 != 0) { // 5보다 작고, 2로 나누어 떨어지지도 않을 때
if (minAns > 0) {
bw.write(ans + minAns -1 + "\n");
} else {
bw.write(-1 + "\n");
}
break;
}
}
bw.flush();
br.close();
bw.close();
}
public static void main(String[] args) throws IOException {
new Main().solution();
}
}
해당 문제를 푸는 데 있어 가장 최적의 답은 5를 많이 사용하는 것이다.
해당 문제의 경우 나올 수 있는 경우의 수를 테스트 케이스를 통해 들어보자.
- 15의 경우
- 5로 나누어 떨어지기에 최적의 수는 3회가 나온다.
- 13의 경우
- 5로도 2로도 나누어 떨어지지 않기에 5를 빼준다.
- 8의 경우 2로 나누어 떨어지기에 별도 4를 저장 해준다. 그리고 5로 빼준다.
- 3의 경우 2로 나누어 떨어지지 않기에 2로 빼준 횟수 4와 5로 빼준 횟수 1을 더해준다.
- 최적의 수는 5가 나온다.
- 14의 경우
- 2로 나누어 떨어지기에 별도 7을 저장 해준다. 그리고 5로 빼준다.
- 9의 경우 5로도 2로도 나누어 떨어지지 않기에 5를 빼준다.
- 4의 경우 2로 나누어 떨어지기에 별도 2를 저장 해준다.
- 최적의 수는 4가 나온다.
다른 이들의 코드 풀이 방식
https://jaewoo2233.tistory.com/55
- 5로 나누어 떨어지지 않으면 2로 빼면서 반복문을 돌려준다.
- 이 때 만약 5로 나누어 떨어지면 횟수를 계산 후 반복문을 종료 해준다.
while(true){ if(N%5 == 0){ count += N/5; System.out.println(count); break; }else{ N -= 2; count++; } if(N < 0){ System.out.println(-1); break; } }
배운 점
- 매번 많은 분기들을 통해 해결 해 나가는 것 같다.
- 그러나 그리디의 경우 분기가 많을 수록 잘못 향하고 있는 가능성이 크다.
- 주어진 테스트 케이스를 통해 수식을 찾아내는 것이 분기를 줄일 수 있는 방법이다.
테스트 케이스를 모두 만족하는 수학식을 찾은 후 코드를 작성하는 습관을 기르자.
