슬라이딩 윈도우와 투 포인터 알고리즘은 선형 공간(1차원 배열)을 2회 이상 반복적으로 탐색해야 할 경우 O(N^2) 이상 걸릴 시간 복잡도를 부분 배열을 활용하여 O(N)으로 줄일 수 있다는 공통점이 있습니다.

두 알고리즘의 차이점은 부분 배열 길이의 변화 여부입니다.

정리하자면 부분 배열의 길이가 슬라이딩 윈도우는 고정적이고 투 포인터 알고리즘은 가변적이라는 것입니다.

🎯 슬라이딩 윈도우

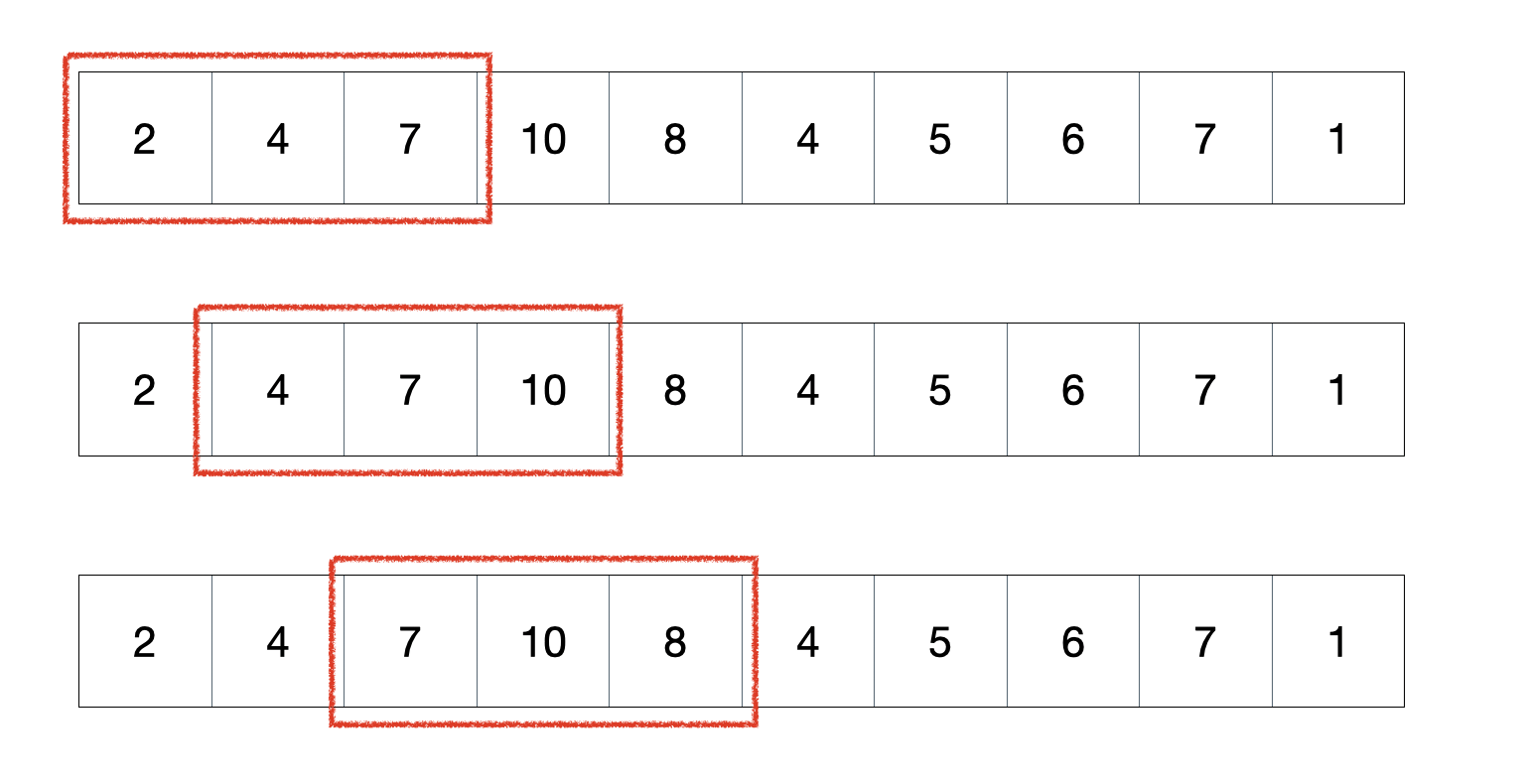
📌 백준 12891번 DNA 비밀번호

import java.io.*;
import java.util.*;

public class DNA비밀번호 {
    static int S, P;
    static String[] DNA;
    static final int Y = 4;
    static int[] standard = new int[Y];
    static String[] ACGT = {"A", "C", "G", "T"};
    static Map<String, Integer> real = new HashMap<>();

    public static void main(String[] args) throws IOException {
        int cnt = 0;
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());

        S = Integer.parseInt(st.nextToken());
        P = Integer.parseInt(st.nextToken());

        DNA = br.readLine().split("");

        st = new StringTokenizer(br.readLine());

        for(int i = 0; i < Y; ++i) standard[i] = Integer.parseInt(st.nextToken());

        for(int i = 0; i < Y; ++i){
            real.put(ACGT[i], 0);
        }

        for(int i = 0; i <= DNA.length - P; ++i){
            if(i == 0) {
                for(int j = 0; j < P; ++j) {
                    real.put(DNA[j], real.get(DNA[j]) + 1);
                }
            } else {
                real.put(DNA[i - 1], real.get(DNA[i - 1]) - 1);
                real.put(DNA[i + P - 1], real.get(DNA[i + P - 1]) + 1);
            }
            if(isOk()) cnt++;
        }

        System.out.println(cnt);
    }

    public static boolean isOk(){
        for(int i = 0; i < Y; ++i){
            if(standard[i] > real.get(ACGT[i])) return false;
        }
        return true;
    }
}

가장 대표적인 유형으로 전형적인 슬라이딩 윈도우 문제의 성격을 띄고 있습니다.

• 단순 선형 탐색으로 일일히 비교하기에는 크기가 매우 크다.
• 주어진 자료의 일부분을 선형적으로 사용하며, 탐색 범위가 고정되어 있다.

✅ 핵심 포인트

1. 인덱스를 사용할 때 OutOfIndex에 주의!

   IDE를 사용하지 못하는 시험에서는 디버깅에 시간을 왕창 날릴 수도 있으므로

   코드가 깔끔하지 못해도 확실하게 범위를 안전하게 잡을 수 있는 코드를 짤 것

2. 투 포인터처럼 변수 두 개를 두고 계속적으로 1씩 증가시키지 않기

   1차원 배열을 예로 들자면 0부터 범위 N까지 지정한다고 했을 때

   idx = 0은 첫 부분 배열을 초기화해주고

   idx = 1부터 양 끝 인덱스에서 1을 빼준 뒤(i, i + N - 1) 비교하는 방식을 사용할 것

🎯 투 포인터

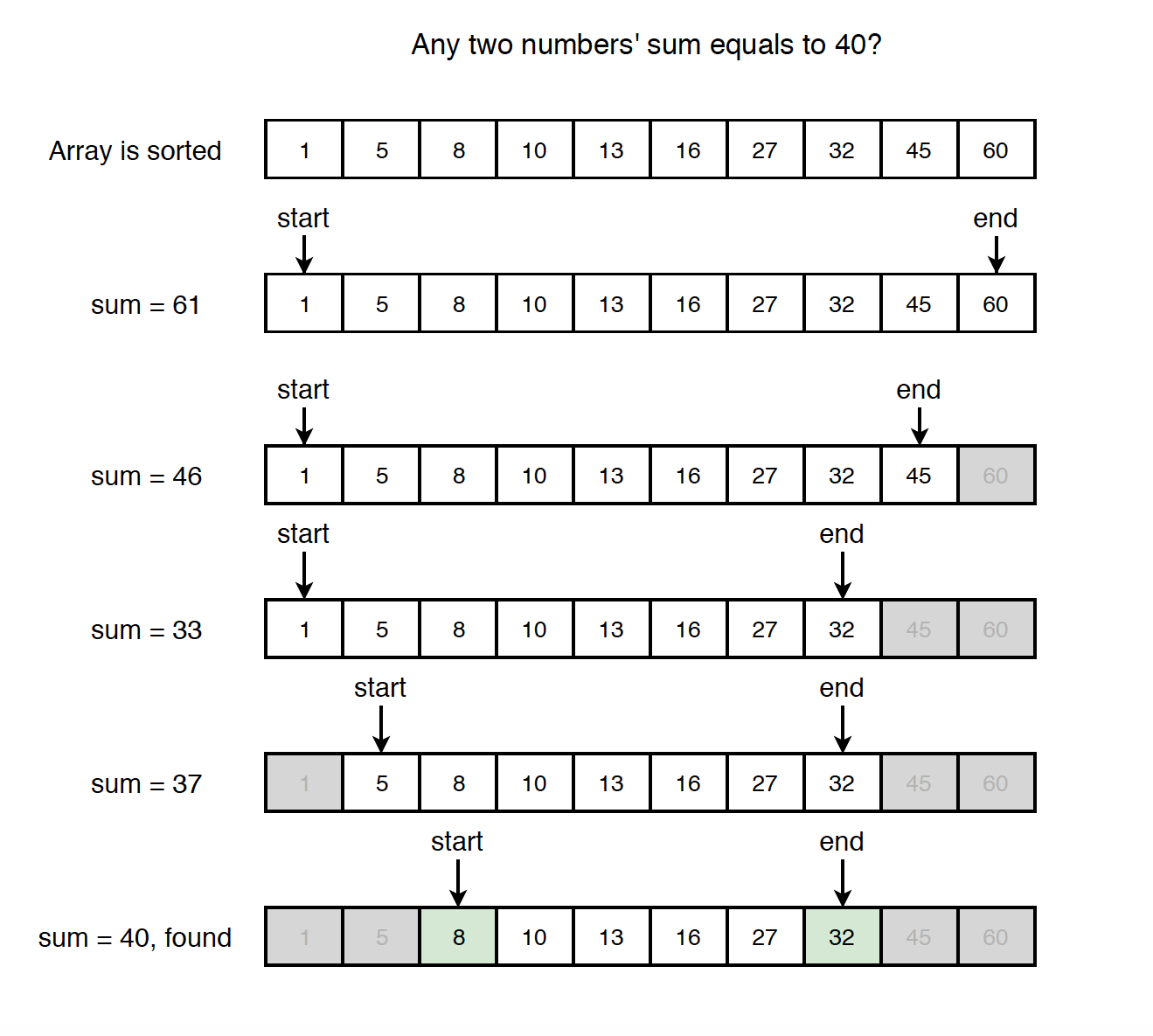
📌 백준 2003번 수들의 합2

import java.io.*;
import java.util.*;

public class Exam2003_수들의합2 {
    static int N, M;

    public static void main(String[] args) throws IOException {
        int cnt = 0;
        int p1 = 0;
        int p2 = 0;
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        int[] num = new int[N];
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; ++i) {
            num[i] = Integer.parseInt(st.nextToken());
        }
        int sum = 0;
        while (p1 <= N - 1) {
            sum += num[p2];
            if (sum == M) cnt++;
            while (sum >= M) {
                sum -= num[p1++];
                if (sum == M) cnt++;
            }
            if(p1 > p2) p2 = p1;
            else if (p2 == N - 1) {
                while (sum >= M) {
                    sum -= num[p1++];
                    if (sum == M) cnt++;
                }
                break;
            }
            else p2++;
        }

        System.out.println(cnt);
    }
}

N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 가장 기본적인 투포인터 문제 입니다.

• 수열의 값이 오름차순이나 내림차순으로 정렬된 아니지만 특정 범위를 지정해서 그 원소들의 합이 M이 되는 경우를 찾아야 합니다.
• 그리고 원소들을 합치는 범위는 가변적입니다.

✅ 핵심 포인트

1. 조합 및 백트래킹과 혼동 주의
   모든 배열의 값들을 필연적으로 탐색하여 특정 조건을 일치시키는 개수 혹은 최저, 최대 값등을 찾는 문제이므로 대게 '조합', '백트래킹'을 떠올리기 쉽습니다. 출제자는 '투 포인터'를 의도하고 출제하기 때문에 시간 초과를 벗어날 순 없을 것 입니다.
2. 인덱스를 사용할 때 OutOfIndex에 주의!
   조건을 잘 설정하여 left 값과 right 값을 적절하게 조절하여 문제가 찾는 값을 찾아주면 됩니다만, 슬라이딩 윈도우와 비슷하게 인덱스 때문에 시간을 잡아먹는 경우가 많습니다.
   깔끔한 코드도 좋지만 코딩 테스트에선 버그가 나지 않도록 확실한 코딩을 하는게 더 중요합니다!