힙 (Heap)

개념

: 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
(** 완전 이진 트리 : 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리)

• 우선순위 큐(Priority Queue)를 구현하기 위해 사용하는 자료구조
  (** 우선순위 큐 : 우선순위가 갖아 높은 데이터를 가장 먼저 삭제하는 자료구조)

• 우선순위 큐 라이브러리에 데이터의 묶음을 넣으면, 첫번쨰 원소를 기준으로 우선순위 설정

힙의 구조

구분	최대 힙 (Max Heap)	최소 힙(Min Heap)
개념	최댓값을 구하기 위한 구조	최솟값을 구하기 위한 구조
조건	각 노드의 값은 해당 노드의 자식 노드 값보다 크거나 같다	각 노드의 값은 해당 노드의 자식 노드 값보다 작거나 같다

시간 복잡도 : $O(logn)$

$n$을 노드의 개수, $h$를 트리의 높이(depth)라 할 때, 힙에 데이터를 삽입하거나 삭제하기 위해서는 최악의 경우 루트 노드에서 단말 노드까지 비교해야 하므로 $h = log_2n$에 가까워진다.
따라서 $O(logn)$의 시간복잡도를 갖게 된다.

힙 vs 이진 탐색 트리

비교	힙(Heap)	이진 탐색 트리(Binary Search Tree)
공통점	이진 트리	이진 트리
차이점	각 노드의 값이 자식 노드보다 크거나 같음 (Max Heap의 경우)	왼쪽 자식 노드 값 < 부모 노드 값 < 오른쪽 자식 노드 값

힙에 데이터 삽입

(1) 기본 동작

힙은 완전 이진 트리의 형태를 갖기 때문에, 삽입할 노드는 기본적으로 왼쪽 최하단부 노드부터 채워진다. 자식노드는 한 부모노드 당 2개씩 채워나간다.

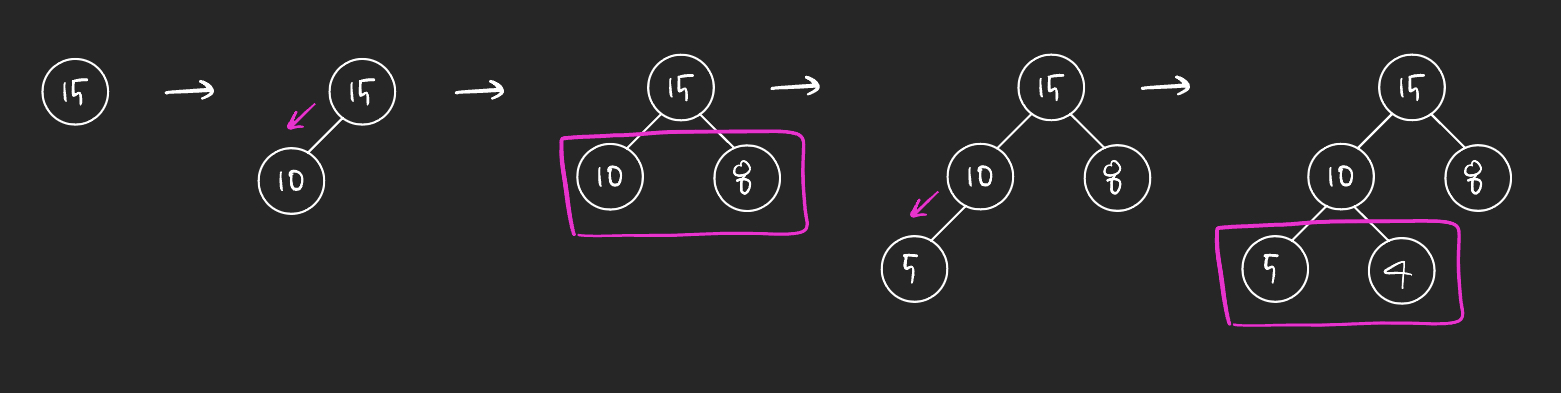
(2) 새로운 데이터 삽입

(Max Heap의 예)

1. 새롭게 삽입된 데이터는 완전 이진 트리 구조에 맞추어 최하단부 왼쪽 노드부터 채워진다.

2. 채워진 노드의 위치에서, 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업(Swap)을 반복한다.

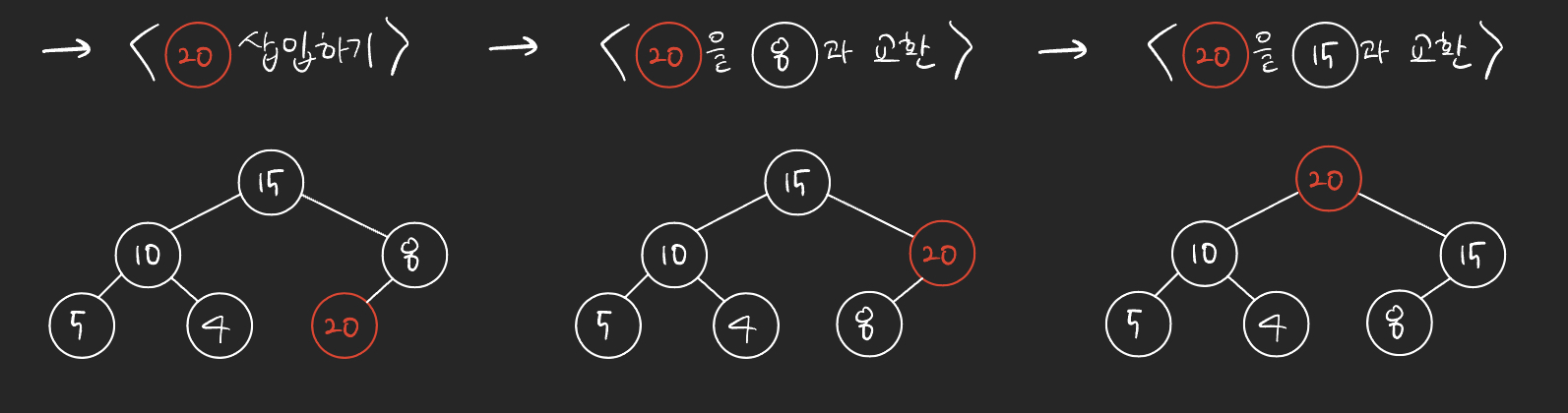
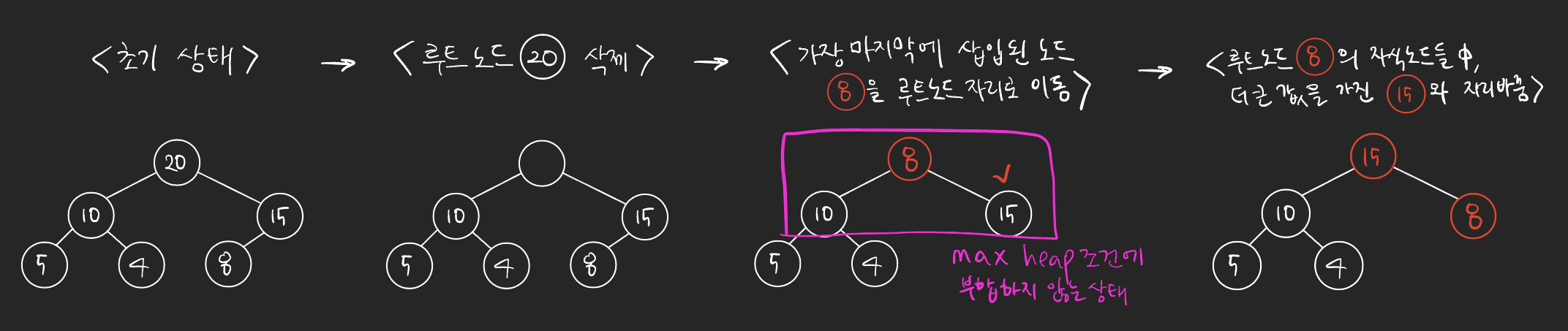
힙에서 데이터 삭제

힙의 용도가 최댓값(or 최솟값)을 루트 노드에 두어서 최댓값(or 최솟값)을 바로 꺼내 쓸 수 있도록 하는 것이기 때문에, 일반적으로 힙에서 데이터 삭제는 루트 노드를 삭제한다.

(Max Heap의 예)

1. 루트노드의 데이터를 삭제한다.

2. 비어있는 루트노드의 자리에, 가장 최하단부 왼쪽에 위치한 노드(일반적으로 가장 마지막에 추가한 노드)를 루트 노드로 이동시킨다.

3. 루트 노드의 값이 자식 노드보다 작을 경우, 루트 노드의 자식 노드 중 가장 큰 값을 가진 노드와 루트 노드의 위치를 바꿔주는 작업(Swap)을 반복한다.

힙 구현

힙은 '완전 이진 트리'의 형태를 띄기 때문에 배열(Array) 자료 구조를 활용하여 구현 가능하다.

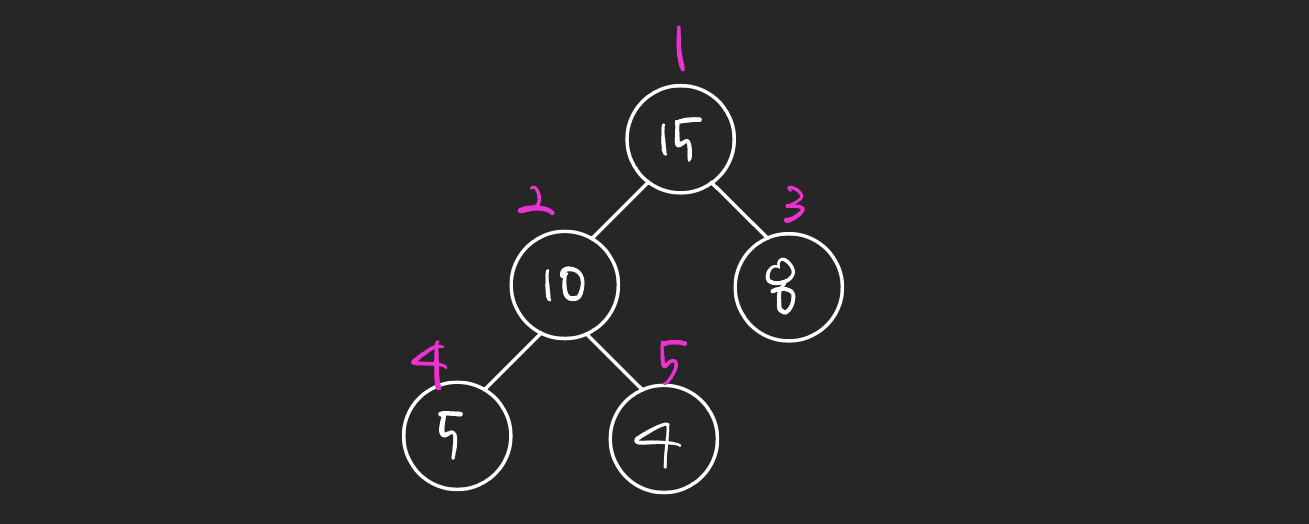
노드 인덱스 설정

배열은 인덱스가 0번부터 시작하지만, 문제에서는 대부분 1번부터 번호를 부여하기 때문에 다음과 같이 설정한다.

• 루트 노드 인덱스 번호 : 1로 지정
• 부모 노드 인덱스 번호 : (자식 노드 인덱스 번호) // 2
• 왼쪽 자식 노드 인덱스 번호 : (부모 노드 인덱스 번호) * 2
• 오른쪽 자식 노드 인덱스 번호 : (부모 노드 인덱스 번호) * 2 + 1

(1) 힙에 데이터 삽입하기

class Heap:
	# 힙 생성 메서드 정의
	def __init__(self, data):
    	self.heap_array = list()
        self.heap_array.append(None) # 인덱스 번호를 1번부터 지정하기 위해서
        self.heap_array.append(data)
    
    # 삽입된 데이터가 부모노드보다 큰 경우 Swap 하는 메서드 정의
    def move_up(self, inserted_idx):
    	if inserted_idx <= 1: # 삽입된 데이터의 인덱스번호가 루트노드가 된 경우 
        	return False # 더이상 swap할 필요가 없으므로 False 반환
		
        parent_idx = inserted_idx // 2 # 부모노드 인덱스 번호
        
        # 삽입된 데이터가 부모노드보다 큰 경우 True 반환, 작은 경우 False 반환
        if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
        	return True
        else:
	    	return False
    
    # 데이터 삽입 메서드 정의
	def insert(self, data):
    	if len(self.heap_array) == 0: # 힙의 길이가 0이면 초기화
        	self.heap_array.append(None)
            self.heap_array.append(data)
            return True
            
        self.heap_array.append(data) # 힙의 길이가 0이 아니라면 왼쪽 최하단 노드에 데이터 추가
        inserted_idx = len(self.heap_array) - 1 # 삽입된 데이터의 인덱스번호
        
        # 삽입된 데이터와 부모노드의 swap 판단 여부가 True이면 swap하기
        while self.move_up(inserted_idx):
        	parent_idx = inserted_idx // 2 # 부모노드 인덱스 번호
            self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx] # swap
            inserted_idx = parent_idx # 인덱스 번호 갱신
        
        return True


# 예제 실행
heap = Heap(15) # 루트노드 15
heap.insert(10)
heap.insert(8)
heap.insert(5)
heap.insert(4)
heap.insert(20)

heap.heap_array

[None, 20, 10, 15, 5, 4, 8]

(2) 힙에서 데이터 삭제하기

class Heap:
	# 힙 생성 메서드 정의
	def __init__(self, data):
    	self.heap_array = list()
        self.heap_array.append(None) # 인덱스 번호를 1번부터 지정하기 위해서
        self.heap_array.append(data)
    
    # 이동시킨 데이터가 자식노드보다 작은 경우 Swap 하는 메서드 정의
    def move_down(self, popped_idx):
    	left_child_popped_idx = popped_idx * 2 # 왼쪽 자식 노드 인덱스 번호
        right_child_popped_idx = popped_idx * 2 + 1 # 오른쪽 자식 노드 인덱스 번호
        
        # (1) 왼쪽 자식 노드가 없는 경우, 거기서 끝
        if left_child_popped_idx >= len(self.heap_array): # array의 길이는 전체 길이 + 1 이므로 없는 곳을 가리키다면
        	return False # False 반환
         
        # (2) 왼쪽 자식 노드는 있는데 오른쪽 자식노드가 없는 경우, 왼쪽 자식 노드와 비교 후 swap	elif right_child_popped_idx >= len(self.heap_array):
        	# 현재 노드가 왼쪽 자식 노드보다 작은 경우 True 반환
        	if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
            	return True
            else:
            	return False
        
        
        # (3) 왼쪽 오른쪽 자식노드가 모두 있을 경우, 더 큰 값을 갖는 자식 노드와 비교 후 swap
        else:
        	# 왼쪽 자식 노드가 오른쪽 자식 노드보다 더 큰 경우
        	if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
            	# 현재 노드가 왼쪽 자식 노드보다 작은 경우 True 반환
            	if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                	return True
                else:
                	return False
            
            # 오른쪽 자식 노드가 왼쪽 자식 노드보다 더 큰 경우
            else:
            	# 현재 노드가 오른쪽 자식 노드보다 작은 경우 True 반환
            	if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
                	return True
               	else:
                	return False
    
    # 힙에서 데이터를 꺼내는 메서드 정의
    def pop(self):
    	if len(self.heap_array) <= 1: # 힙에 데이터가 없는 경우
        	return None
            
    	returned_data = self.heap_array[1] # 꺼낼 최상단 노드 변수 설정
        self.heap_array[1] = self.heap_array[-1] # 비어있는 루트노드 자리에 가장 마지막에 추가한 노드로 갱신
        del self.heap_array[-1] # 이동시킨 공간 지워주기
        
        popped_idx = 1 # 이동시킨 데이터의 인덱스 번호 (1: 루트노드로 올라가야 함)
        
        # 이동시킨 데이터와 자식노드의 swap 판단 여부가 True이면 swap하기
        while self.move_down(popped_idx):
    		left_child_popped_idx = popped_idx * 2 # 왼쪽 자식 노드 인덱스 번호
        	right_child_popped_idx = popped_idx * 2 + 1 # 오른쪽 자식 노드 인덱스 번호
        
	        # (2) 왼쪽 자식 노드는 있는데 오른쪽 자식노드가 없는 경우, 왼쪽 자식 노드와 비교 후 swap		
            if right_child_popped_idx >= len(self.heap_array):
        		if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
            		self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx] # swap
                    popped_idx = left_child_popped_idx # 인덱스 번호 갱신
        
        	# (3) 왼쪽 오른쪽 자식노드가 모두 있을 경우, 더 큰 값을 갖는 자식 노드와 비교 후 swap
        	else:
        		if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
            		if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                		self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx] # swap
                        popped_idx = left_child_popped_idx # 인덱스 번호 갱신

            	else:
            		if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
                		self.heap_array[popped_idx], self.heap_array[right_child_popped_idx] = self.heap_array[right_child_popped_idx], self.heap_array[popped_idx] # swap
                        popped_idx = right_child_popped_idx # 인덱스 번호 갱신
                        
        return returned_data
        
# 위의 예제에 이어서 실행
heap.pop()      

20

🔗 References

패스트캠퍼스 - 개발자 취업 합격 패스 with 코딩테스트, 기술면접