[자료구조]이진 인덱스 트리(펜윅 트리)

이진 인덱스 트리

구간합을 $O(logn)$이내에 구할 수 있는 자료구조입니다.

---

그러면 이런 이진 인덱스 트리를 사용하는 이유는 무엇일까요?

다음과 같은 배열 A가 주어졌다고 가정해 봅니다.

A

1

2

0

4

1

3

5

9

8

6

이 때, $PrefixSum(k)= A[i] + ... + A[k]$라 정의할 때, $1 \le k \le n$이므로 시간 복잡도는 $O(n)$으로 구간합을 구할 수 있습니다.

만약, 이런 $PrefixSum$을 $m$번 구할 경우, 시간 복잡도는 $O(mn)$이 되게됩니다.
하지만 전처리과정을 통해 시간 복잡도를 $O(m+n)$으로 줄일 수 있습니다.

전처리 과정을 저장할 배열 P를 선언하고 $P[k] = A[1] + ... + A[k]$를 저장하면 다음과 같이 배열 P가 주어집니다.

P

1

3

3

7

8

11

16

25

33

39

따라서 이제 $O(n)$이 걸리던 구간합을 $O(1)$안에 바로 구할 수 있습니다.

예를 들어 $PrefixSum(5)$를 구할 경우 $PrefixSum(5) = A[1] + ... + A[5] = P[5] = 8$임을 바로 알 수 있습니다.

다음과 같이 A 배열의 구간 5~8위치의 합을 $Sum(5,8) = A[5] + ... + A[8]$이라 할 때, 마찬가지로 시간 복잡도 $O(1)$에 구할 수 있습니다.

$Sum(i,j) = A[i] + ... + A[j] = P[j] - P[i-1]$이므로 전처리과정을 통하여 시간복잡도 $O(1)$로 빠르게 구할 수 있음을 알 수 있습니다.

하지만 만약 A배열의 5번째 위치의 값이 1이 아닌 3으로 바뀌게 된다면 구간합을 구하는 전처리 배열을 다시 구해 주어야 합니다.

이런 배열의 k위치의 값을 x로 바꿔주는 함수를 $update(k,x)$라 하고 다시 전처리 배열을 구하는데 걸리는 시간복잡도는 $O(n)$입니다.

이 때, Binary Index Tree를 사용할 경우, $update(k,x)$가 수행될 때, 다시 전처리 배열을 $O(logn)$에 구할 수 있습니다.

---

이진 인덱스 트리로 사용할 배열 T를 먼저 선언해줍니다.

$PrefixSum(6) = (A[6] + A[5]) (+ ... + A[2] +A[1])$
$T[6] = A[6] + A[5]$
$T[4] = A[4] +A[3] +A[2] + A[1]$

$prefixSum(10) = A[10] + ... A[1]$
$T[10] = A[10] + A[9]$
$T[8] = A[8]+ ... + A[1]$

그리고 다음 수식처럼 T의 각 위치에 A배열의 구간합을 나누어 넣어줄 것입니다.

그러면 각 위치에 저장할 구간합을 어떻게 나누어 저장해야 할까요?

바로 $T[k] = A[k] +... +A[k-LSB(k)+1]$ 와 같이 저장합니다.

이 때, $LSB(k)$는 $k$를 비트로 나타냈을 때, 오른쪽끝에서 왼쪽끝으로 이동하면서 처음 1이 등장하는 위치가 d일 때, $2^d$로 구해줍니다.

따라서, $k=6$일 때, 비트로 표현하면 110 이고, 처음 1이 등장하는 위치인 d는 1이므로 $LSB(6) = 2^1 =2$가 됩니다.

그러므로 $T[6] = A[6] + ... +A[6-2+1] = A[6] + A[5]$가 저장되게 하면 됩니다.

이대로 T 배열을 모두 구하면 다음과 같이 구해집니다.

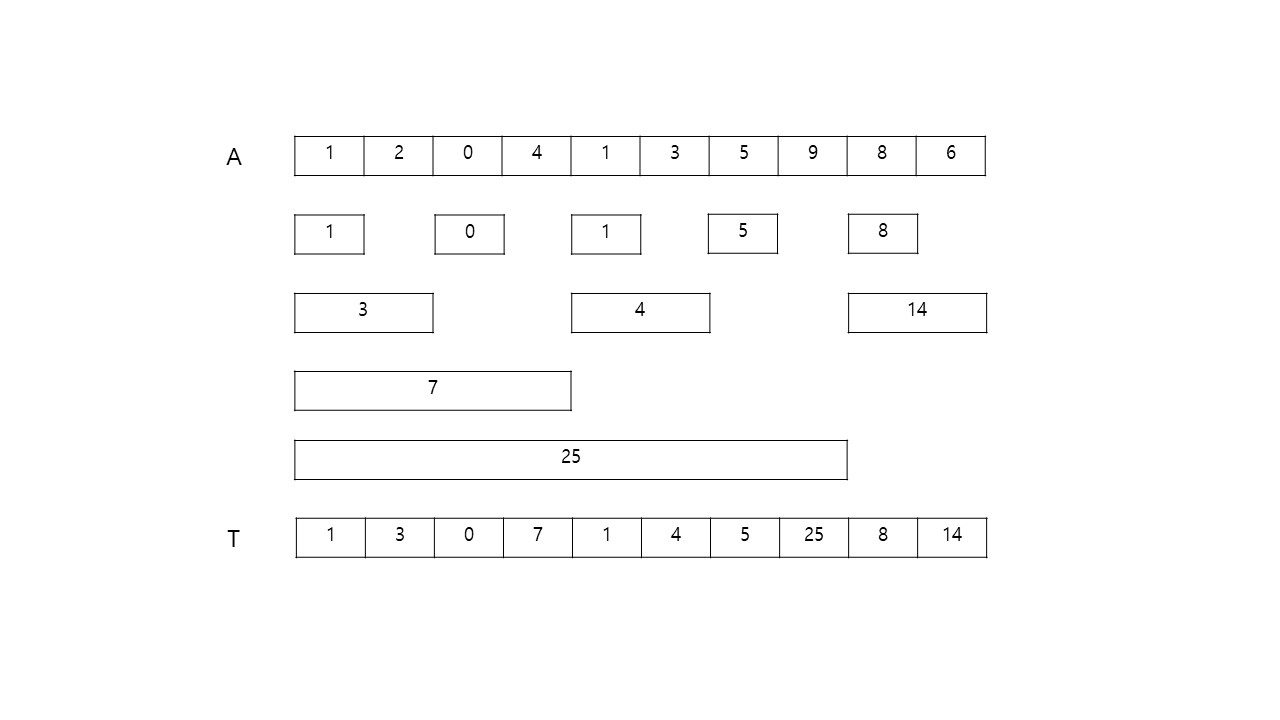
그러면 $LSB(k)$의 시간복잡도는 과연 어떻게 될까?

$LSB(k)$를 구하는데 오래 걸리면 효율적이지 못하므로 먼저 $LSB(k)$의 시간 복잡도를 구해봅니다.

다음과 같이 비트가 01101000인 k가 주어졌다고 가정해봅니다.

이 때, k의 2의 보수 (= 1의 보수 +1)를 구하면 $10010111 +1 = 10011000$입니다.

이를 k와 &연산하면 $k\&-k= 0001000$로 상수시간 안에 $LSB(k)$를 구할 수 있음을 알 수 있습니다.

그러면 T에 저장된 각 구간의 합을 이용하여 어떻게 원하는 구간의 합을 구할 수 있을까요?

배열 T를 보면 각 누적합이 트리 형태와 유사하게 저장되어 있습니다.

이 때, 각 누적합은 LSB를 사용하여 구간을 나누었으므로 구하고자 하는 $PrefixSum(k)$를 구할 때, 시작 위치를 k로 두고 k에서 $LSB(k)$를 계속 빼주어 k값이 0이 될 때까지 T배열의 위치를 이동시키면서 각 구간의 합을 합해주면 구할 수 있습니다.

def prefix_sum(k):
  s = 0
  while k>=1:     # 1의 개수만큼 복잡도를 가짐, k<=n, O(log n)
    s= s+T[k]
    k = k - LSB(k)
  return s

마찬가지로 배열의 값이 변경되었다면,

def update(k,x): #A[k] -> x로 체인지
  d= x-A[k]
  while k <= n:
    T[k] = T[k] + d
    k = k + LSB(k)

따라서 이진 인덱스 트리(펜윅트리)를 사용할 경우, 각 구간 합과 구간의 변경을 $O(logn)$에 구할 수 있습니다.