union-find

찬밥·2024년 8월 24일

목록 보기

1/1

union-find 알고리즘이란?

여러개의 노드가 존재할 때, 두 노드를 선택해 같은 그래프의 노드인지 확인하고 합치는 알고리즘

Union

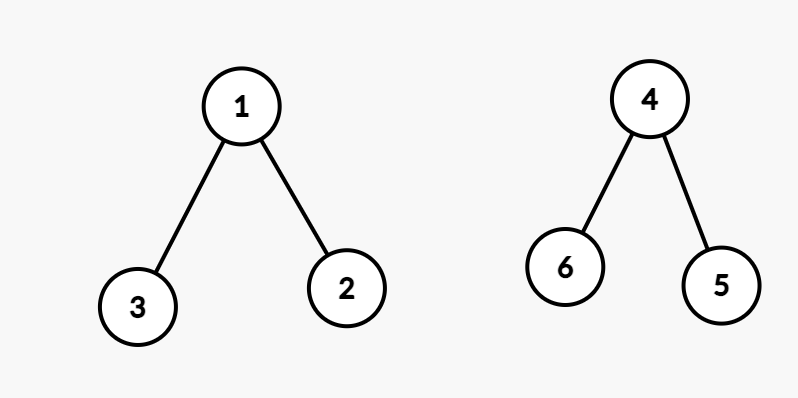
두 트리를 합치는 과정

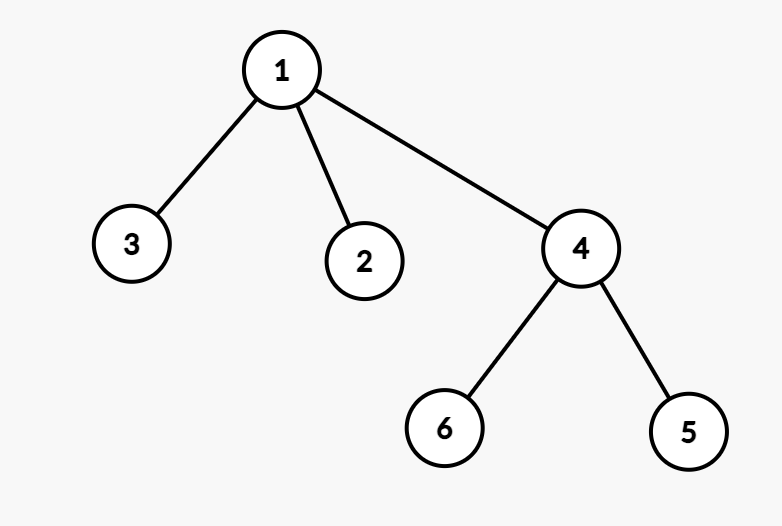
위 그림과 같이 루트가 4와1인 두 그래프가 있을 때, 한 그래프로 합치는 과정

⇒ 한 그래프의 루트노드를 다른 그래프의 자식으로 넣어줌

보통의 경우 부모가 작은 수를 가지게 union 한다.

Find

두 노드가 같은 그래프에 속하는지 확인하는 과정

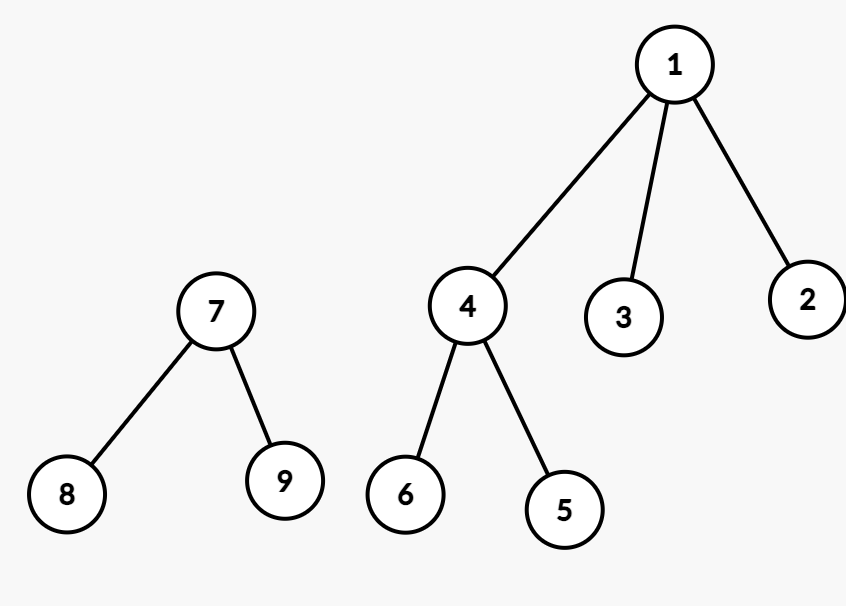
9와 6는 같은 그래프인가? → 놉

why? 루트가 다르기 때문

그런데.. 그래프의 깊이가 깊어질수록 부모를 찾는데 오래 걸리네..?

나는 이 작업을 여러번 해야하는데 너무 비효율 적인 것 아냐..?

⇒ 루트를 찾고, 루트의 자식이 되자!

경로 압축

find 과정에서 루트 노드를 찾는 과정에서 지나는 모든 노드들을 루트의 자식으로 만듦

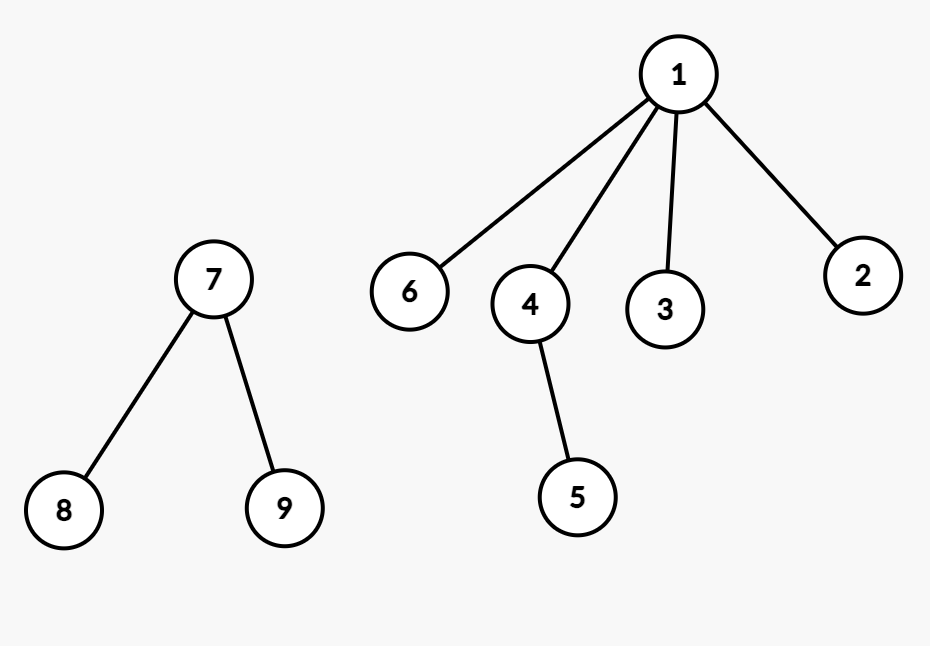
오호! 다음 번에 6를 조사할땐 빠르게 루트를 찾을 수 있겠다!

경로 압축을 하지 않을 경우 최악의 경우 O(N)의 복잡도를 가짐

{1} ← {2} ← {3} … ← {n}

구현 방법

크게 배열과 트리 방법이 있는데, 배열이 간단해서 보통 배열을 활용함

5의 경우 부모가 루트가 아니므로 find 연산시 부모가 1로 경로 압축될 예정
6과 9를 비교해보면 부모(루트)가 다르므로 다른 노드임!

구현

int find(int n){
	if(p[n] == n) return n;
	return p[n] = find(p[n]); //경로압축
}

void uni(int a, int b){
	A = find(a);//A의 root를 찾음
	B = find(b);//B의 root를 찾음
	if(A==B) return;//A와 B가 같으면 같은 그래프이므로
	if(A < B) p[B] = A;
	else p[A] = B;
}