[백준 11049] 행렬 곱셈 순서

https://www.acmicpc.net/problem/11049

험난했던 시험 기간을 끝내고 다시 돌아온 백준 시간. 오늘 푼 문제는 알고리즘 시간에 배운 행렬곱셈 순서를 실제로 풀어본 문제이다. 현재 학교 알고리즘 과목에서 DP를 배우고 있다.

풀이 방법

우선 행렬의 곱셈 성질에 대해서 알아야 한다.
행렬 A(p*q) 와B(q*r)를 곱하면 총 연산은p*q*r이고, AB크기는p*r이 된다.

이를 인지했으니, 본격적으로 시작해보자.
$A_1$부터 $A_n$까지의 행렬이 존재하였을 때, $A_n$이 가능한 곱셈의 연산 횟수는 n-1이다.
$(A_1 * A_2 .. A_{n-1}) * A_n$
$(A_1 * A_2 .. A_{n-2})(A_{n-1} * A_n)$ 등등..

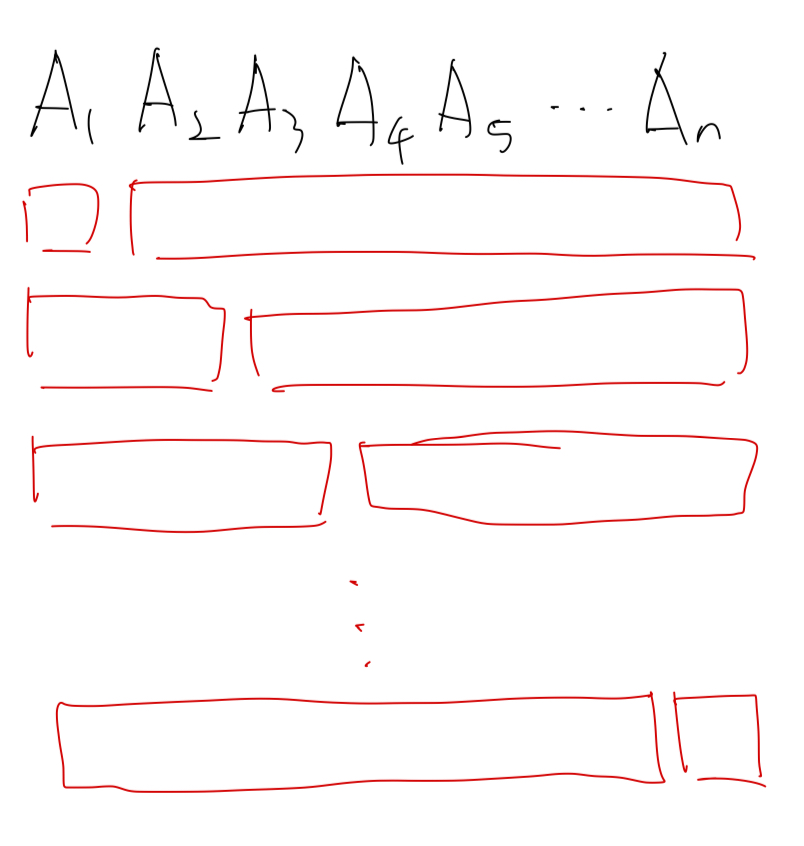
이 중 가장 연산 횟수가 적은 값을 찾으면 된다는 것이다.
그렇다면 $(A_1 * A_2 .. A_{n-1})$의 값은? 마찬가지로 n-2의 경우의 수 중에서 가장 작을 값을 ... 이렇게 계속 내려가 재귀적으로 구할 수 있다.
그러나, 정말 재귀적으로 풀기에는 경우의 수도 많고, 중복된 내용도 많다.
또한 큰 문제를 해결하기 위해, 작은 부분을 해결하는 최적 부분 구조도 가지고있다. 그러므로 DP를 사용해서 풀어야 한다.

최적부분 구조

$A_i$ ~ $A_j$까지의 최소 연산을 $C_{i~j}$라고 한다면,

$C_{i~j}$는 임 의의 K(i<=k<=j-1)을 기준으로 $C_{i~k}$ + $C_{k+1~j}$ + 두 행렬의 곱셈 연산 수이다.

예) $C_{1~4}$를 구할 때, $C_{1~2}$와 $C_{3~4}$를 가지고 구함 (1=A 2=B 3=C 4=D)

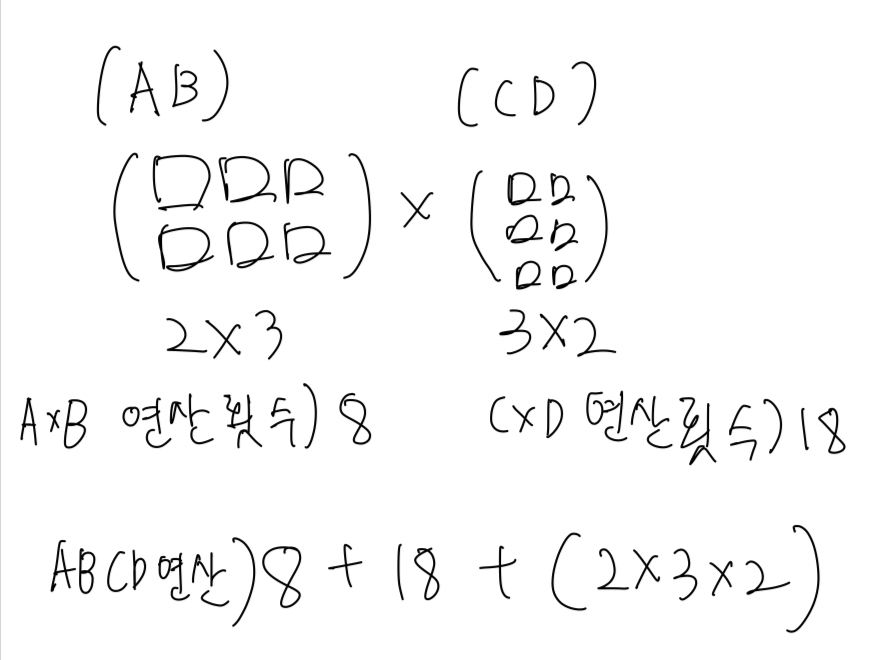
즉,

이 된다. 이제 연산을 구해보자.
우선, 행렬의 곱의 특징은, 곱하려는 AB의 행과 열이 같아야 한다.
즉, 겹치는 부분이 존재한다. $A_1$~$A_4$까지의 행렬이 있으면 p*q q*r r*x x*z
이렇게 행렬이 겹친다. 중복된 부분을 제거해보자.

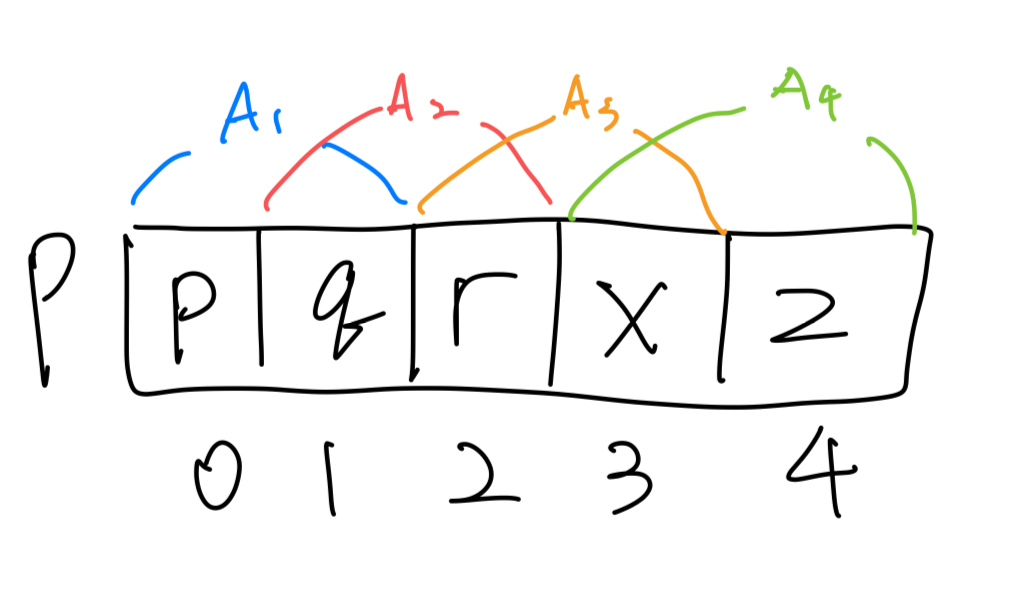
$A_i$의 행은 i-1, 열은 i가 됨을 알 수 있다.이를 연산에 집어 넣어보면 $P_{i-1}P_{K}P_{j}$가 된다.(만약 이부분이 이해가 안된다면 행렬을 곱했을 때, 연산 후 행렬의 크기가 p*r임을 잊지 말자)

후, 이제 최적부분 구조도 알았겠다,이제 아래서부터 차근차근 올라가보자
그룹의 체인(괄호로 묶는 묶음)은 자기 자신~n개까지 즉, 1개,2개..n개만큼 묶을 수 있다.
나 자신만을 묶는다면 $C_{i~i}$가 될 것이고, 2개를 묶는다면 $C_{i~i+1}$이 될 것이다.결국i~j까지의 원소가 모두 묶일때까지 반복한다.

시간복잡도
체인의 길이n 행렬의 개수n

코드

import java.util.Scanner;

public class Main {


    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int[] p= new int[n+1];
        for(int i=1;i<=n;i++){
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            p[i-1]=a;
            p[i]=b;
        }
        int[][] m = new int[n+1][n+1];
        for(int i=1;i<=n;i++){
            m[i][i] = 0;
        }
        for(int r=2;r<=n;r++){
            for(int i=1;i<=n-r+1;i++){
                int j =i+r-1;
                int minValue = Integer.MAX_VALUE;
                for(int k=i;k<=j-1;k++){
                    minValue = Math.min(minValue,m[i][k]+m[k+1][j]+(p[i-1]*p[k]*p[j]));
                }
                m[i][j] = minValue;
            }
        }
        System.out.println(m[1][n]);
    }
}