Algorithm 개념

위상 정렬에 대해 설명하기 전에, 먼저 DAG에 대해서 알아야한다.
❓ DAG (Directed Acyclic Graph) ?
DAG는 순환을 가지지 않는 방향 그래프를 의미한다.
일반적으로 우선순위를 가진 일련의 작업들은 DAG 구조를 가진다.
ex) 대학 과정의 선수과목, 스타 크래프트에서 건물 짓는 순서…
위상 정렬은,
- DAG (비순환 방향 그래프)에서 그래프의 방향성을 거스르지 않고 정점을 나열하는 것
- 위상 정렬은 각 정점을 우선순위에 따라 배치한 것
- 위상 정렬의 결과는 유일하지 않다. ⇒ 시작 정점은 선택하기 나름이고, 방향성만 지키면 되기 때문이다
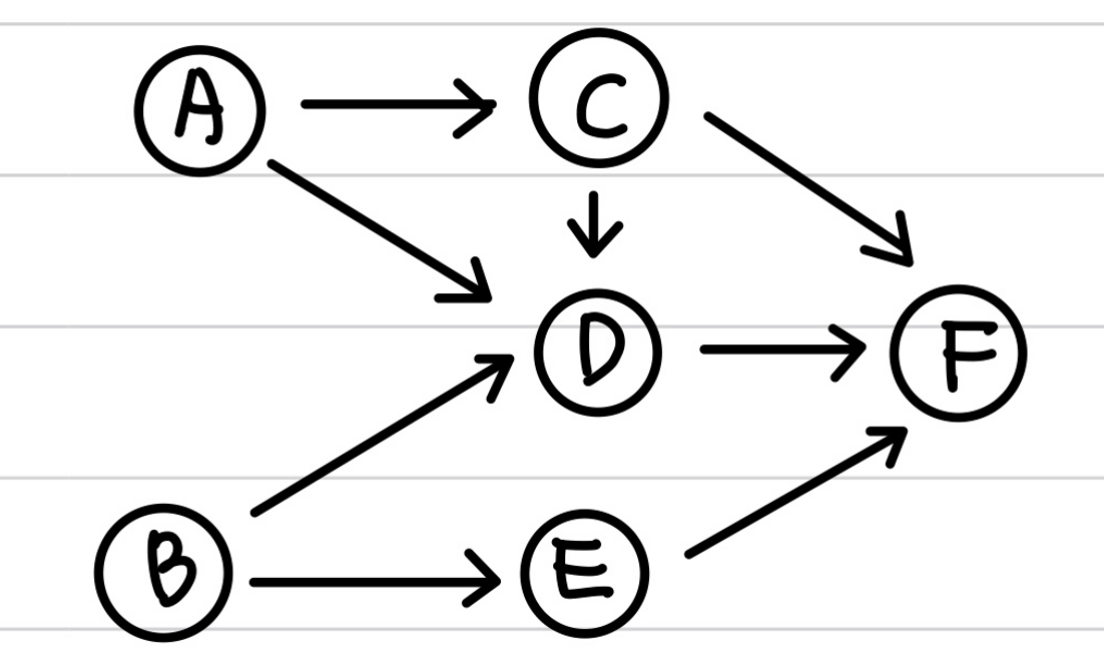
다음과 같은 그래프를 예시로 보자.
<A, B, C, D, E, F> 와 <B, A, E, C, D, F>와 같은 순서는 위상 정렬이 된다.
하지만 <C, A, B, D, E, F>는 방향성이 A 다음 C 이기 때문에 위상 정렬이 아니다.
자, 이제 위상 정렬이 대충 어떤 것을 의미 하는 것인지 알았으니 위상 정렬 알고리즘을 알아보자 !
먼저, 진입 차수라는 개념을 알아두도록 하자.
앞으로 얘기하는 진입 차수란 그 정점으로 들어오는 정점의 개수를 의미한다.
즉, 선행되어야하는 정점의 개수를 뜻한다. 위에 그림에서 D 정점 같은 경우는 D 이전에 실행되어야하는 정점은 A, C, B 세 개 이므로 D의 진입 차수는 3이 된다.
진입 차수가 0이라는 것은 선행되어야하는 정점이 없는 정점이란 뜻이기 때문에, 시작 정점이 된다.
따라서,
진입 차수가 0인 정점을 선택하고 선택된 정점과 연결된 모든 간선을 삭제한다.
이때, 삭제되는 간선과 연결된 정점들의 진입 차수를 변경해주고
이 과정을 반복해서 모든 정점을 출력하면 알고리즘이 끝난다.
말로는 잘 이해가 안될 수도 있으니, 한 스텝씩 그림과 함께 설명하겠다 !
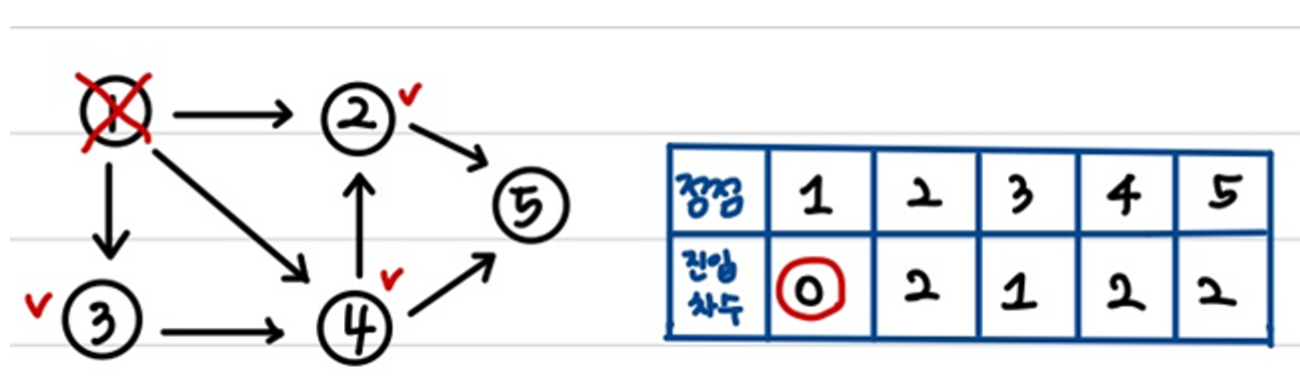
1) 진입 차수가 0인 정점 1번이 시작 정점이 된다. 1번 정점과 연결된 정점은 2번, 3번, 4번이므로 이 정점들의 진입 차수를 바꿔주고, 정점 1번을 삭제한다.
1번 →
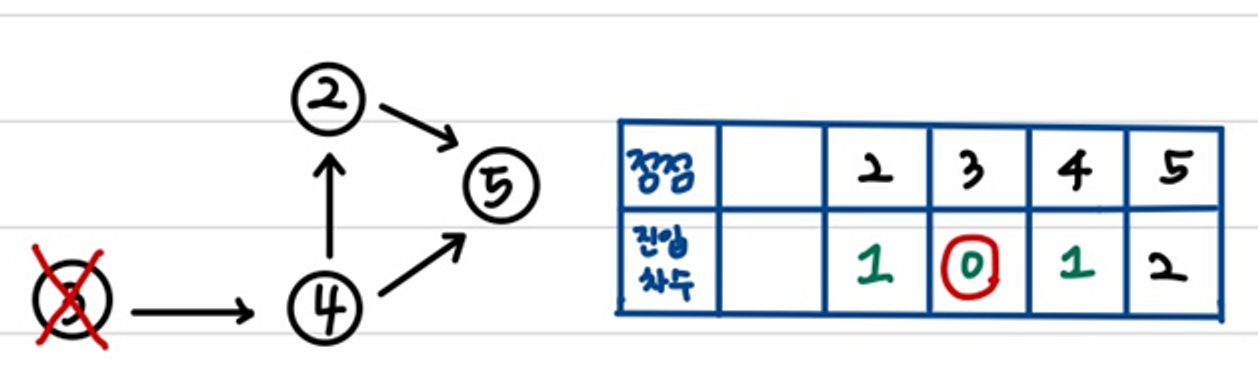
2) 진입 차수가 바뀐 것은 초록색으로 표시했다. 위와 마찬가지로 이제는 정점 3번의 진입 차수가 0이므로 그 다음은 정점 3번을 선택한다. 3번과 연결된 정점 4번의 진입 차수를 바꿔주고 정점 3번을 삭제한다.
1번 → 3번
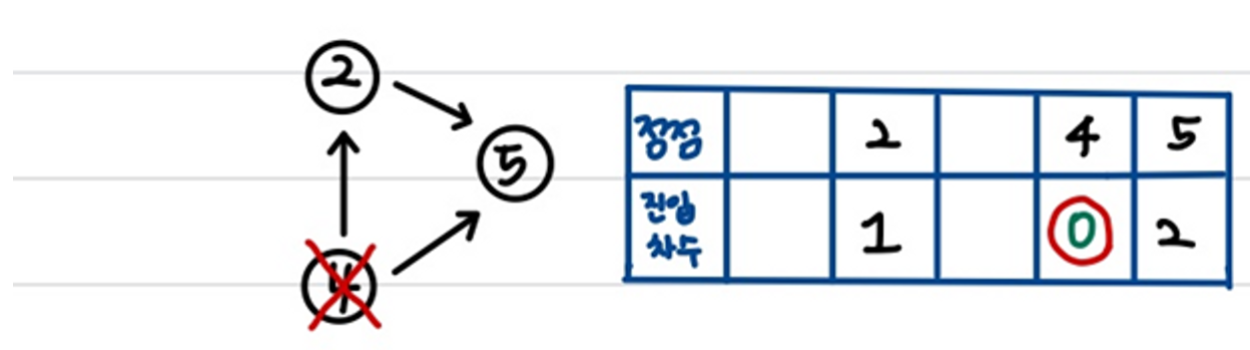
3) 위와 마찬가지로 진행해준다. 정점 4번 선택.
1번 → 3번 → 4번
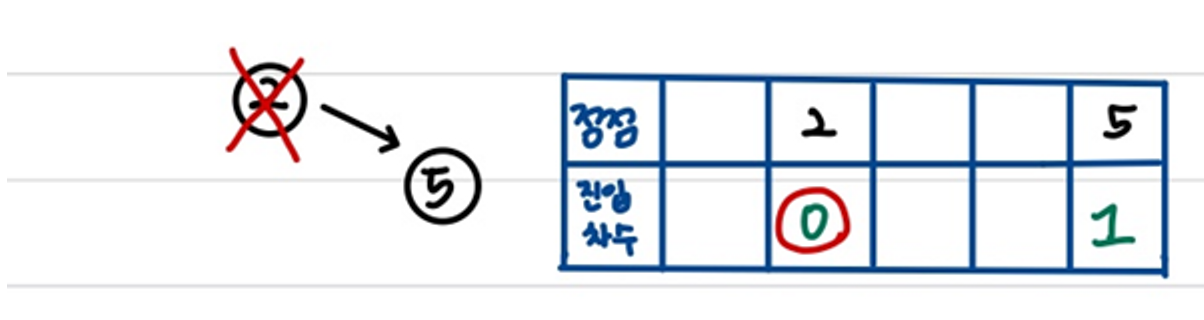
4) 위와 마찬가지로 진행해준다. 정점 3번 선택.
1번 → 3번 → 4번 → 2번
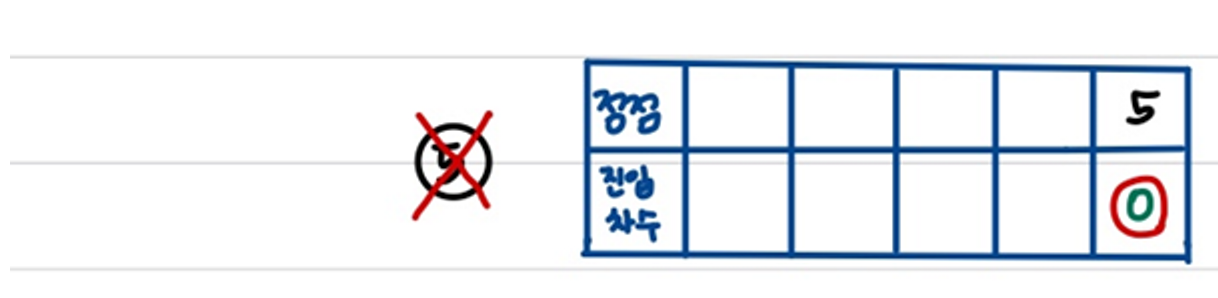
5) 마지막 정점까지 모두 삭제하면 알고리즘이 끝난다.
1번 → 3번 → 4번 → 2번 → 5번
정리하면,
- 각 노드마다 자신으로 향하는 노드의 개수를 저장 ( 진입 차수 ⇒ 1차원 배열 indegree )
- 탐색 노드에서 출발하여 도착하는 노드의 indegree를 하나씩 빼준다.
- indegree가 0인 경우엔 선행되어야하는 정점이 없는 것이므로 queue에 저장하여 출발 노드로 이용한다.
- queue가 빌 때까지 탐색을 진행한다.
순서로 코드를 작성하면 된다.
실제 코드를 어떻게 작성하여 문제를 해결하는 것인지 궁금하다면
밑에 달아놓은 페이지를 참고하면 좋을 것 같다 !
👇 위상 정렬과 관련된 백준 문제 풀이
