자료구조 빨리 후다닥 복습

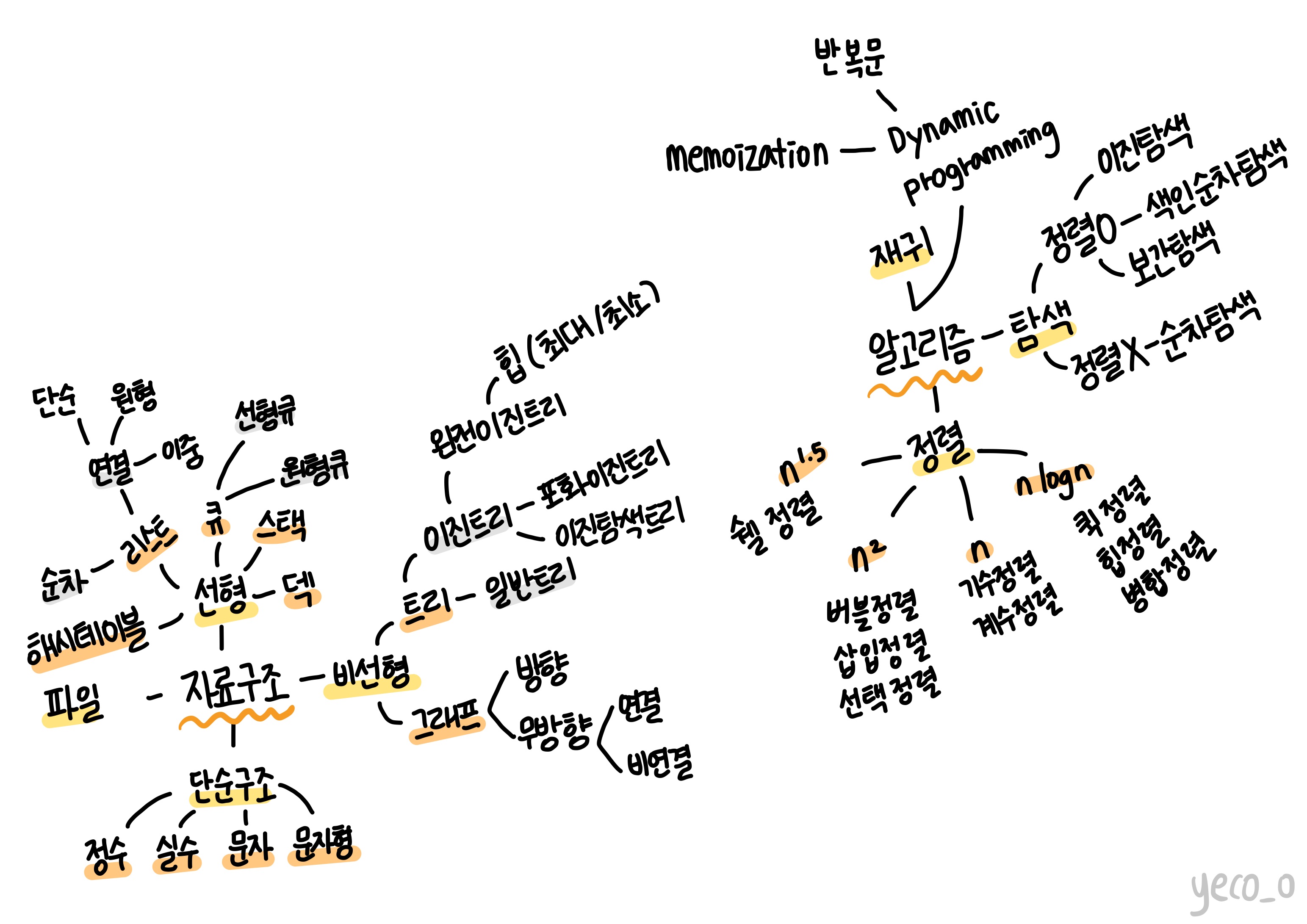
자료구조에 대해 전반적인 개념 위주로 적은 글입니다 ✍(◔◡◔)

배열과 연결리스트

📍배열

동일한 타입의 데이터를 연속적인 메모리 공간을 할당받아 저장하는 자료구조. 인덱싱이 되어있어 인덱스 번호로 특정 데이터에 빠르게 접근이 가능하다.

하지만 삭제, 삽입을 할 때는 데이터를 이동해줘야 하므로 시간이 더 걸린다.

📍리스트

1. 배열로 구현된 리스트

장점: 구현이 간단하다. 특정 인덱스로 접근이 빠르다.

단점: 리스트의 크기가 고정되어 데이터를 추가할 때 남는 공간이 없다면 문제가 생긴다. 기존의 배열을 복사하여 더 큰 배열을 넣는 것은 CPU 낭비이다.
또한 리스트 중간에 삽입, 삭제는 기존의 데이터를 이동해야 한다.

2. 연결 리스트

배열과 달리 연속적이지 않은 메모리 공간을 할당 받는다. 각 노드가 데이터와 포인터를 가지고 연결되어 있는 자료구조. 포인터는 다음 노드를 가리킨다. 첫 노드를 알아야 전체 노드에 접근이 가능하기 때문에 첫 노드를 가리키는 헤드 포인터가 있다.

장점: 크기가 제한되지 않고 중간에서 삽입, 삭제를 빠르게 할 수 있다.

단점: 구현이 복잡하고 임의의 항목을 추출할 때 배열보다 오래 걸린다. 노드(포인터)를 생성하여 순회하며 노드를찾는 과정을 반복하기 때문이다.

💡종류

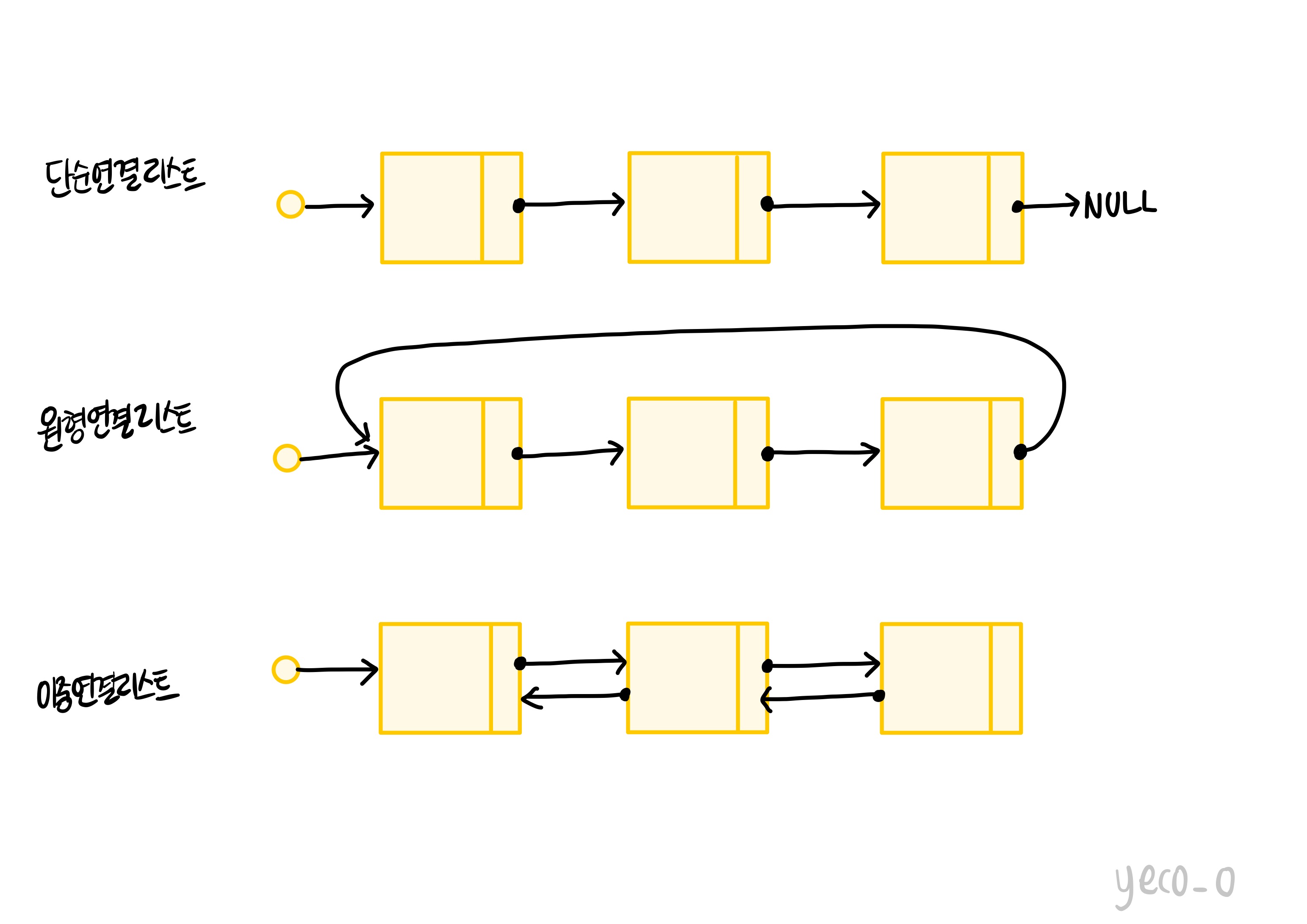
단순 연결리스트: 하나의 방향으로 연결되어 마지막 노드는 NULL값을 가리킨다.
원형 연결리스트: 마지막 노드가 첫 번째 노드를 가리킨다. 즉 하나의 노드에서 모든 노드로 접근할 수 있다.
이중 연결리스트: 양방향 연결. 즉 선행 노드, 후행 노드를 전부 가리킨다.

스택과 큐

*추상적 자료구조란?
스택, 큐는 일종의 규칙이다. 자료구조의 방법이 코드로 정의된 게 아니라 행동 양식만 정의된 것이다. 즉 규칙만 이해한다면 배열, 연결리스트로 구현할 수 있다. 추상적 자료구조의 장점은 정보 은닉, 코드의 재사용, 가독성, 사용자의 유연성(다형성) 등이 있다.

📍스택

💡특징

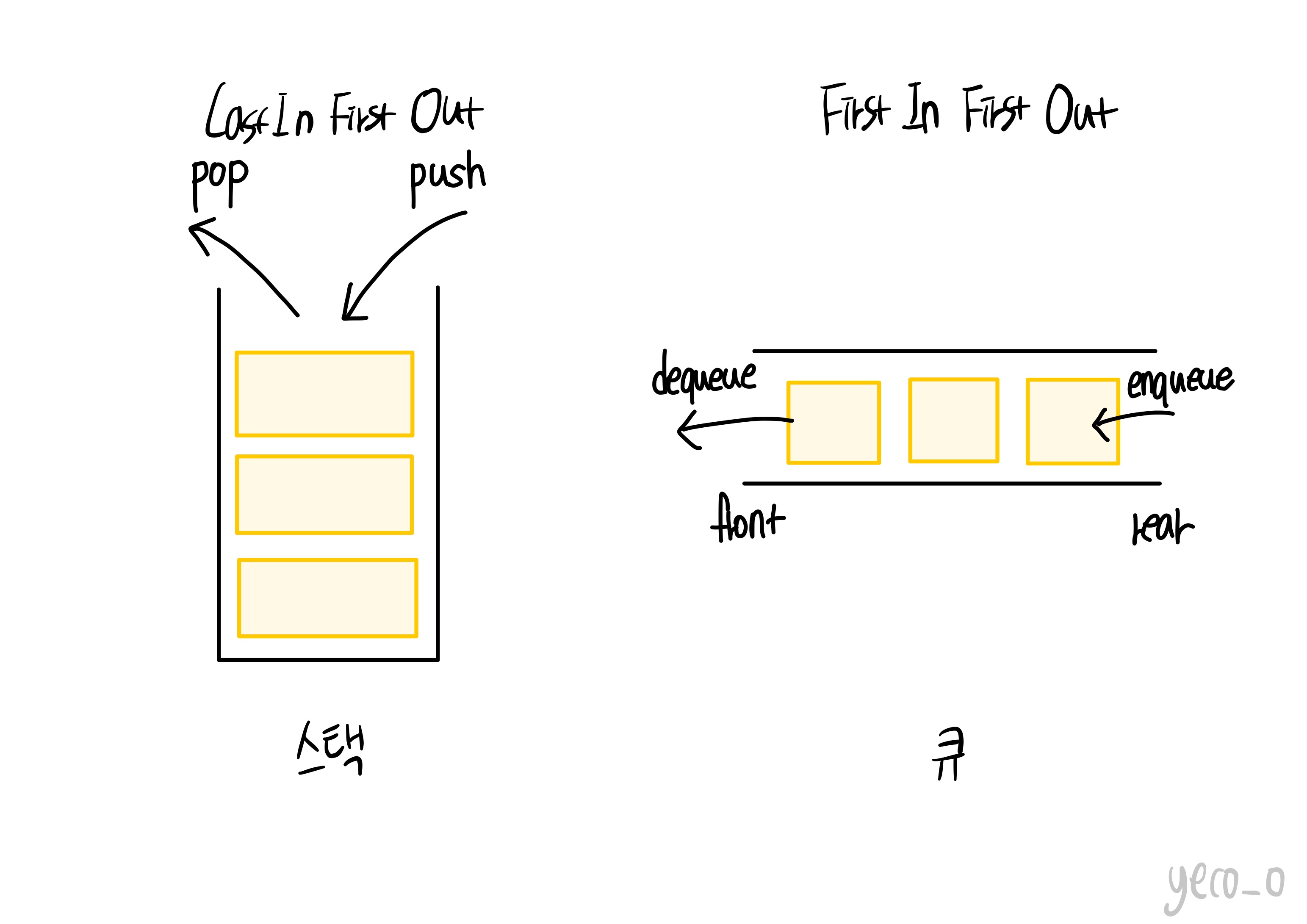
후입선출(LIFO)로 가장 나중에 들어온 데이터가 먼저 나간다. top에서 삽입 연산 push와 삭제 연산 pop이 이루어진다.
뒤로가기 버튼을 누를 때, 후위 표기법 계산, 깊이 우선 탐색 등에 쓰인다.

💡구현

배열이나 연결리스트로 구현하며 top은 배열로 구현하면 전역 변수, 연결리스트로 구현하면 포인터변수가 된다.

📍큐

💡특징

선입선출(FIFO)로 가장 먼저 들어온 데이터가 먼저 나간다. front에서 삭제연산 dequeue, rear에서 삽입연산 enqueue가 이루어진다. CPU와 주변기기 사이의 버퍼 역할, 너비 우선 탐색, 기수 정렬 등에 쓰인다.

💡구현

배열이나 연결리스트로 구현하며 선형 큐, 원형큐마다 다르다.
배열로 구현 시 1차원 배열을 이용하며 front, rear은 전역 변수로 선언된다. 크기가 제한되고 연속적인 메모리 공간을 할당 받는다.

연결리스트로 구현 시 동적 메모리 할당을 해야해서 코드가 더 복잡하고 오래 걸린다. 큐에 요소가 없는 경우 front와 rear은 NULL값을 가리킨다. 크기에 제한이 없다.

1. 선형 큐

-front, rear의 초기값은 -1에서 증가만 한다. 삭제연산 후 배열의 앞 부분이 비어 주기적으로 요소들을 이동시켜야 한다는 단점이 있다.

2. 원형 큐

-front, rear의 초기값은 0이다. 선형큐와 달리 front는 첫 번째 요소의 하나 앞을, rear는 마지막 요소를 가리킨다.
-즉 fronr == rear 는 공백 상태, front == (rear+1)/MAX_QUEUE_SIZE 는 포화 상태이다.
-원형으로 만들기 위해 나머지 연산자(%)를 사용한다.
-선형 큐의 단점을 보완하여 원형이므로 배열의 요소를 옮겨주지 않아도 된다.

트리

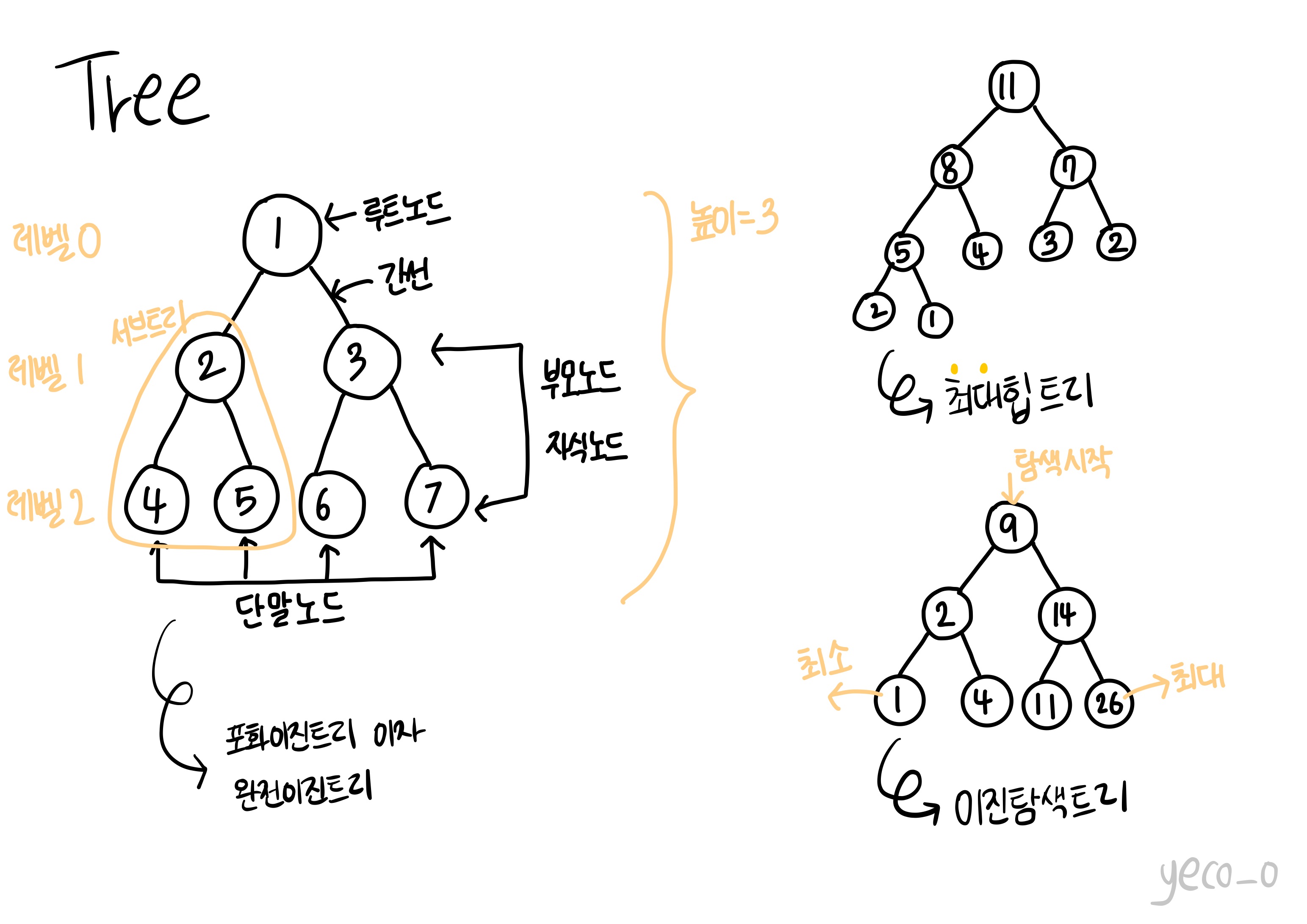
📍트리

계층적인 자료구조로 루프나 사이클이 없는 게 특징이다. 일종의 사이클이 없는 연결 그래프. 루트에서 어떤 노드로 가는 길은 유일하며 n개의 노드를 n-1개의 간선으로 연결한다는 특징이 있다.

1. 일반 트리

각 노드가 서로 다른 수의 자식노드를 가진다. 즉 링크필드의 개수가 달라져 노드의 크기가 고정되지 않는다.

2. 이진 트리

💡특징

모든 노드가 2개의 서브트리를 가진다. 서브 트리는 각각 왼쪽, 오른쪽으로 순서가 존재하며 공백노드도 자식노드로인정한다. 포화 이진트리, 완전 이진트리로 나눌 수 있다.

💡종류

-포화 이진트리: 각 레벨에 노드가 꽉 차있는 이진트리.
-완전 이진트리: 마지막 레벨은 왼쪽에서 오른쪽으로 순서대로 차있는 이진트리.
-포화 이진트리는 항상 완전 이진트리지만 그 역은 성립하지 않는다.

💡구현

1. 배열을 이용한 방법

   -포화 이진트리, 완전 이진트리에서 많이 사용한다. 이진 트리의 높이가 k일 때 2^k-1개의 공간을 연속적으로 할당 받은 다음 노드의 순서대로 저장한다.
   -장점: 배열의 인덱스로 부모 노드, 자식 노드를 쉽게 찾을 수 있다.
   -단점: 일반 이진트리의 경우 메모리 공간의 낭비가 생길 수 있다.

2. 링크를 이용한 방법

   -트리의 노드가 구조체로 표현된다. 이진 트리의 경우 데이터 필드 1개와 왼쪽, 오른쪽 자식 노드를 가리키는 포인터 필드 2개로 이루어진다. 즉 루트 노드를 가리키는 포인터만 있으면 전체 노드로 접근이 가능하다.
   -연결 리스트와 유사한데 연결 리스트는 1차원적 구조라면 링크로 표현된 트리는 2차원적 구조라 할 수 있다.

💡순회방법

1. 전위 순회: 루트노드 > 왼쪽 서브트리 > 오른쪽 서브트리
2. 중위 순회: 왼쪽 서브트리 > 루트노드 > 오른쪽 서브트리
3. 후위 순회: 왼쪽 서브트리 > 오른쪽 서브트리 > 루트노드

이 3가지가 가장 대표적인 이진트리 순회 방법이다. 스택을 사용한다. 자식 노드를 먼저 방문해야하는 경우 후위 순회를 사용한다. 예를 들어 현재의 디렉토리 용량을 계산할 때 하위 디렉토리 용량을 우선 알아야 하기 때문에 사용한다. 이 외에도 레벨을 기준으로 순회하는 레벨 순회가 있다. 레벨 순회는 큐를 사용한다.

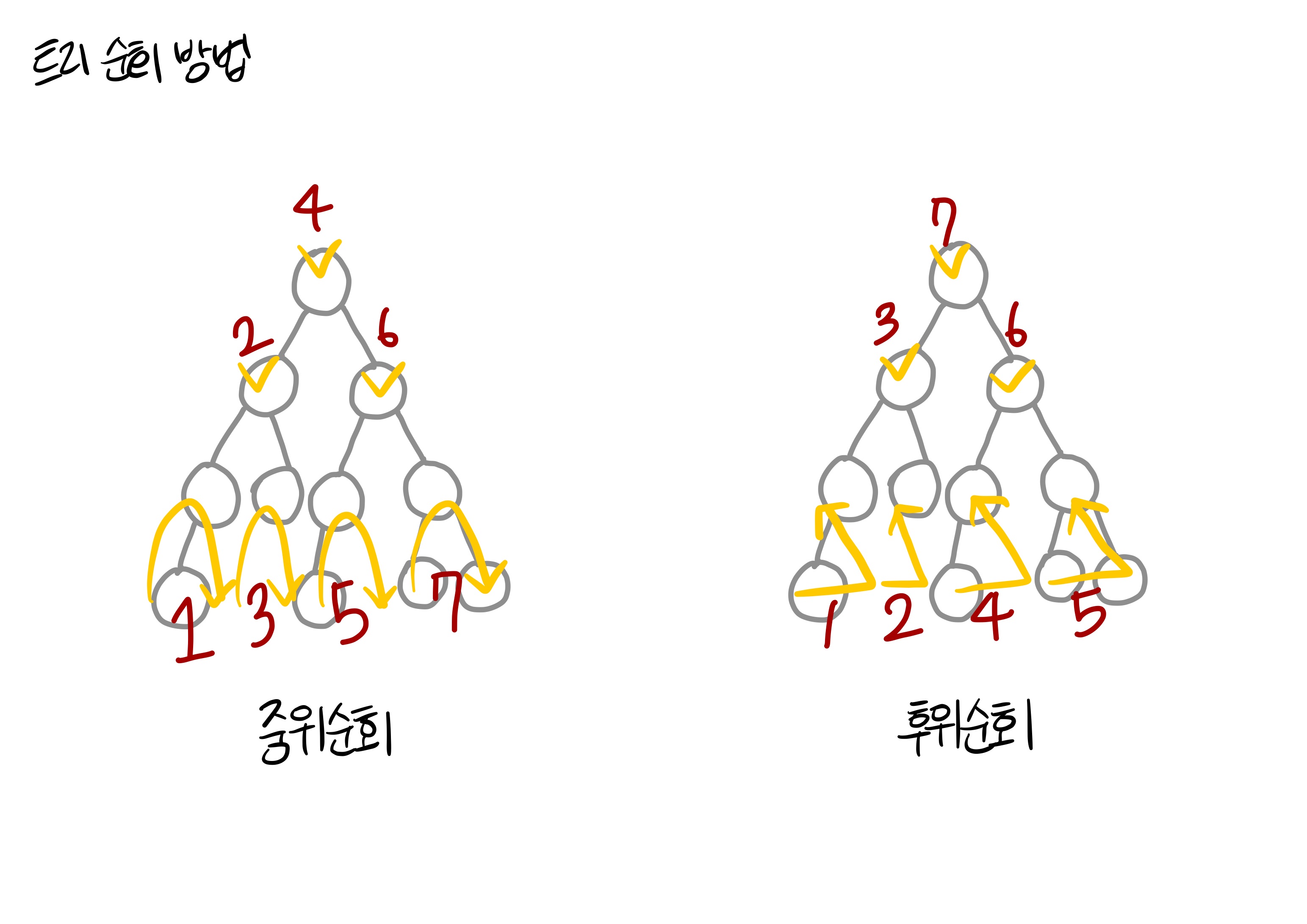
(트리 순회 방법 꿀팁 그린 건데... 딱 저 순서만 외운다면 면접에서 1초컷으로 술술 나옵니다. (내가 만들었지만 정말 와편함) 빨리 와다다 말하려면 어디 되돌아가서 저쩌고 생각할 시간이 없으니 :) 최대한 쉽게 그렸는데 효과가 있을랑가...)

3. 이진 탐색 트리

💡특징

이진트리 기반의 탐색을 위한 구조이다. 모든 원소는 유일한 키를 가지며 왼쪽 서브트리의 키는 오른쪽 서브트리의 키보다 작다는 특징이 있다. 이러한 특징으로 탐색을 효율적으로 할 수 있다.
최솟값은 트리의 마지막 레벨 왼쪽 노드이미 최댓값은 오른쪽 노드이다.

💡구현

효율적으로 탐색하기 위해 포인터를 사용한다. 힙트리는 완전 이진트리이기 때문에 배열을 사용하지만 이진 탐색 트리는 이진트리이므로 배열을 사용하기 어렵다.
탐색할 땐 주어진 탐색 값과 루트 노드의 값을 우선 비교한 후 다음 과정이 나뉜다. 값이 같다면 탐색이 성공으로 끝난다. 루트노드가 더 크다면 왼쪽, 더 작다면 오른쪽으로 이동한다.

이렇게 탐색할 때 이진트리의 균형이 중요하다. 균형트리가 아니라면 같은 노드의 수라도 비교 횟수에 차이가 생긴다.

4. 히프

💡특징

힙은 우선순위 큐를 구현하기 위해 만들어진 자료구조이다. 우선순위 큐란 데이터들이 우선순위를 가지고 순서대로 삭제되는 자료구조이다. 이를 구현하는 가장 효율적인 방법이 힙(히프)이다.

히프는 완전 이진트리의 일종이다. 이진 탐색 트리와 달리 중복되는 값을 허용한다는 특징이 있으며 느슨한 정렬 상태를 유지한다. 힙의 목적은 가장 큰 값, 가장 작은 값 몇 개를 찾기 위함이기 때문이다.

💡종류

최대 힙: 부모 노드의 키가 자식 노드의 키보다 항상 큰 힙.
최소 힙: 부모 노드의 키가 자식 노드의 키보다 항상 작은 힙.

💡구현

힙트리는 완전 이진트리의 일종이므로 배열을 이용해 구현한다.

그래프

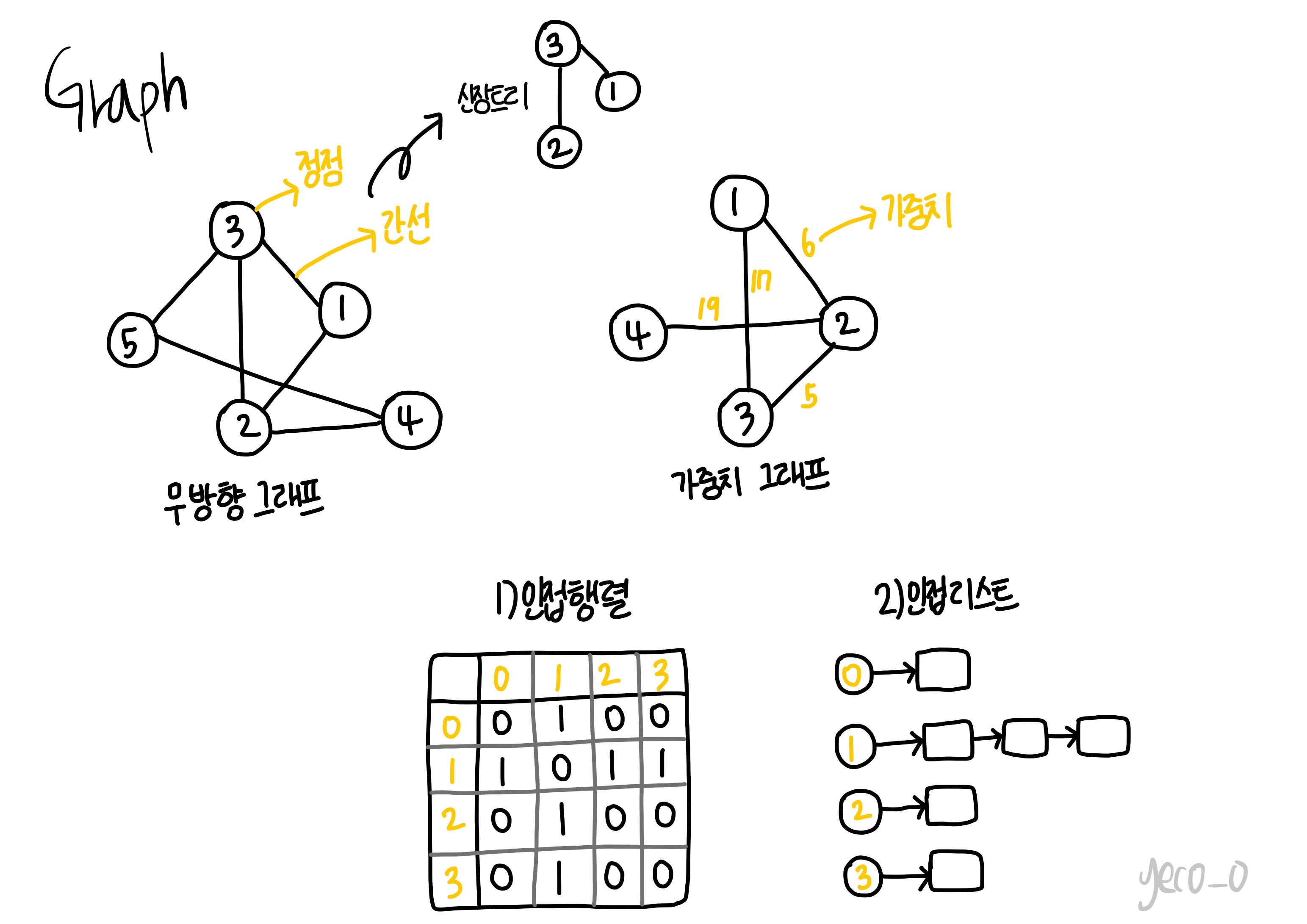
📍그래프

그래프는 지도처럼 복잡한 객체 사이를 표현할 수 있는 자료구조이다. 정점과 간선의 유한집합이다.

💡종류

방향 그래프: 간선에 방향성이 존재
무방향 그래프: 간선이 양방향으로 연결
연결 그래프: 무방향 그래프에 있는 모든 정점쌍에 항상 경로 존재
비연결 그래프: 연결 그래프가 아닌 것
가중치 그래프(네트워크): 간선에 가중치를 할당
등등

💡구현

1. 인접 행렬
   -2차원 배열인 인접행렬은 불리언 행렬로 0, 1로 이루어진다. 간선이 존재한다면 1 아니면 0이다. 무방향 그래프의 경우 행렬은 대칭을 이루게 된다. 즉 상위 삼각, 하위 삼각만 저장하면 메모리의 낭비를 줄일 수 있다.
   간선의 수와 상관 없이 정점의 제곱만큼 공간이 필요하다. 즉 희소 그래프의 경우 부적절하다.
   -특정 간선의 유무는 O(1)로 즉시 알 수 있지만 전체 간선의 수는 O(노드^2)만큼 시간이 걸린다.

2. 인접 리스트
   -각각의 정점에 연결된 정점을 포인터로 연결해 연결 리스트로 표현한 것이다. 각 연결 리스트는 헤더노드를 가지고 있고 이는 배열로 구성되어 있어 정점이 번호를 인덱스의 번호로 사용한다면 각 정점의 연결 리스트에 쉽게 접근할 수 있다.
   -실제로 연결된 노드만 저장하기에 실제 간선에 비례하는 메모리만 사용한다.
   -인접 행렬과 달리 특정 간선의 유무를 알기 위해서는 O(간선)만큼 시간이 걸리지만 전체 간선의 수는 더 빨리 알 수 있다.
   -희소 그래프의 경우 효율적이다.

📌그래프 탐색 알고리즘

그래프 탐색이란 하나의 정점으로부터 모든 정점을 한 번씩 방문하는 것이다. 대표적인 방법으로 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)가 있다.

1. 깊이 우선 탐색
   순환 알고리즘, 스텍을 이용한다. 다음 분기로 넘어가기 전 해당 분기를 전부 탐색하는 방법이다. 트리를 탐색할 때 한 방향으로 쭉 가다가 막히면(NULL) 최근의 갈림길로 돌아가는 것과 유사하다. 모든 노드들을 방문하고자 할 때 사용한다.

2. 너비 우선 탐색
   큐를 이용한다. 탐색할 때 인근한 정점을 먼저 방문하는 기법으로 최단 경로를 찾고자 할 때 사용한다. 깊이 우선 탐색과 달리 재귀적으로 작동하지 않는다.

📌신장트리

신장트리는 최소의 간선으로 그래프를 연결하는 트리이다. 트리의 특수한 형태로 모든 정점을 연결하며 사이클을 포함해선 안 된다. n개의 정점을 n-1개의 간선으로 연결한다. 즉 하나의 그래프에는 많은 신장트리가 존재할 수 있다.

여기서 간선의 가중치까지 고려하여 최소 비용으로 연결하는 것을 최소 비용 신장트리라고 한다. 즉 그래프의 모든 정점을 가장 작은 간선의 가중치로 연결하며 사이클을 포함하지 않는 것이다.

최소 비용 신장 트리 알고리즘

1. Kruskal의 MST 알고리즘
   탐욕적인 방법으로 매순간 최선의 선택을 한다. 그래프의 간선들을 오름차순으로 정렬한 후 최소 비용의 간선 부터 선택하여 집합에 추가한다. 이때 추가하는 간선의 양 끝 접점이 집합에 존재한다면 사이클을 이루므로 주의한다. 이때 union-find알고리즘을 사용한다.
   간선 정렬에 Kruskal알고리즘의 시간 복잡도가 좌우 된다. 즉 간선의 수가 작은 희소 그래프의 경우 적절하다.

2. Prim의 MST 알고리즘
   시작 정점으로부터 최소 가중치로 연결된 인근 정점을 선택해 집합에 추가하는 방법이다. 즉 정점 위주의 알고리즘이며 기존의 집합을 사이클을 이루지 않게 확장해나가는 방식이다. 시작 단계에서는 시작 정점만 집합에 있다. 이렇게 확장하는 과정을 총 정점의 수가 n일 때 n-1개의 간선을 가질 때까지 반복한다. 이중 반복문으로 O(n^2)의 시간 복잡도를 가진다. 정점 위주이기 때문에 간선의 수가 많은 경우 적절하다.

해시 테이블

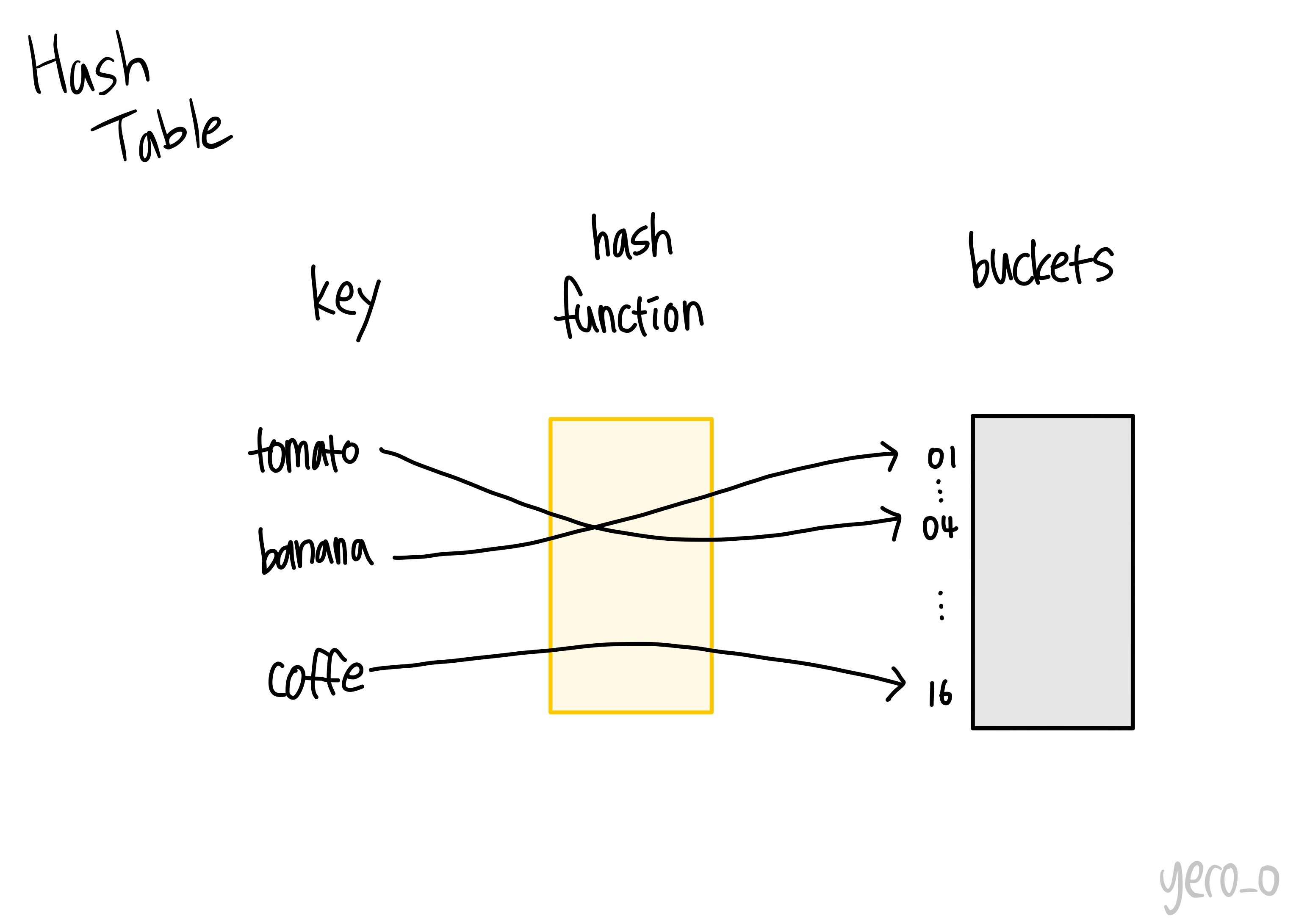
📍해시 테이블

해시 테이블은 Key Value 시스템을 이용해 자료를 정리한다. 해시 테이블을 이용한 탐색을 해싱이라고 하는데 해싱에서 자료를 저장할 때는 배열을 이용한다. 배열에서는 요소의 인덱스값만 알면 자료를 빠르게 찾을 수 있기 때문이다.

💡해시 함수

해시 함수는 저장하고자 하는 key를 고유의 인덱스로 바꾼 후 그 곳에 데이터를 저장한다.

해시 함수는 입력 길이와 상관 없이 랜덤값을 출력하며 일방향적이고 동일한 입력에 대해서는 동일한 출력을 한다. 좋은 해시 함수이기 위해서는 충돌이 적어야 하고 해시 테이블 내에 고르게 분포되어야 하며 계산이 빨라야 한다.

💡해시 함수의 종류

-제산 함수: 나머지 연산자를 이용하여 주소를 계산하는 방법
-폴딩 함수: 레코드의 키를 마지막 부분을 제외하고 동이한 길이로 나눈 후 합하거나 배타적 논리합을 취해 주소로 사용하는 방법
-중간 제곱 함수: 키를 제곱하고 중간의 몇 비트를 주소로 사용하는 방법
-비트 추출 방법: 해시테이블의 크기가 2^k일 때 이진수로 간주해 임의의 k개 비트를 해시 주소로 사용하는 방법
-숫자 분석 방법: 숫자로 구성된 키에서 각 수의 특징을 알고 있을 때 사용한다. 예를 들어 학번이 20191934일 때 편중되지 않도록 입학년도인 2019를 빼고 나머지 수를 조합해 주소로 사용하는 방법
-기수 변환 방법: 주어진 키를 다른 진법으로 변환하여 주소로 사용하는 방법

💡충돌 해결 방법

서로 다른 키에 대하여 해시 함수가 같은 주소를 준 경우를 충돌이라고 한다. 이 충돌이 버킷의 슬롯 수 보다 많이 일어나면 오버플로우가 발생하는데 버킷 1개에 슬롯이 1개인 경우는 충돌이 곧 오버플로우를 의미한다. 이때 충돌을 해결하는 방법으로 개방 주소법과 체이닝이 있다.

이런 충돌 문제 때문에 해시 테이블이 항상 상수시간 O(1)인 건 아니다.

1. 개방 주소법
   개방 주소법은 충돌이 일어났을 때 비어있는 버킷을 찾는 방법이다. 이 과정을 조사 또는 탐색이라고 한다.

선형 조사법은 비어있는 공간이 나올 때까지 순차적으로 조사한다. 일차 군집화 문제에 취약하다는 문제점이 있다.

제곱 조사법, 이차 조사법은 탐사폭을 제곱으로 늘린다는 점에서 위와 차이가 있다. 연쇄적 충돌의 가능성이 줄어든다.

이중 해싱, 재해싱은 해시 함수를 두 번 사용하는 것이다. 하나는 주소값을 구할 때, 하나는 탐사폭을 구할 때이다. 이 방법은 다양한 탐사폭을 제공하므로 골고루 저장될 확률이 높아진다.

2. 체이닝
   체이닝은 버킷이 하나 이상의 값을 저장하도록 연결 리스트를 이용한다. 즉 사용하지 않은 버킷을 찾아야만 끝나는 개방 주소법의 문제점을 보완한 것이다. 버킷 내에서 항목을 찾을 땐 순차탐색한다.

---

편입 준비하면서 공부했던 자료구조 코드 없이 핵심 부분만 추려서 정리해봤는데 오류가 있다면 알려주세요 (☞ﾟヮﾟ)☞ 💭🔊