📍재귀란?
재귀 알고리즘이란 하나의 함수에서 자기 자신을 다시 호출하여 문제를 해결하는 알고리즘입니다. 재귀로 문제를 풀기 위해선 평소의 절차 지향적 사고가 아닌 귀납적 사고를 해야합니다. 즉 전제가 결론을 개연적으로 뒷받침하는 것입니다.
📍재귀 함수의 특징
재귀 함수는 한 단계 낮은 문제가 해결되면 그것을 바탕으로 답을 얻을 수 있습니다. 그러기 위해선 무한 루프에 빠지지 않기 위해 아래 조건을 꼭 만족해야 합니다.
✔ 재귀호출 시 인자는 반드시 규모를 줄이도록 변화
✔ 재귀호출 없이 해결 가능한 최소의 문제 넣기
위의 조건들을 통해 함수 내의 재귀 호출이 중단되며 문제가 해결 됩니다. 함수의 인자로 어떤 것을 받을지, 어디까지 계산 후 자신에게 다시 넘길지 또한 명확하게 적어야 합니다.
📍동적 계획법이란?
동적 계획법(Dynamic Programming)이란 큰 문제를 작은 문제로 나누어 해결하면서 반복되는 연산 값을 저장해두었다 꺼내 쓰는 방법입니다. 즉 하나의 문제는 한 번만 풀면서 재귀 함수의 계산 복잡도를 해결할 수 있습니다.
동적 계획법은 크게 2가지로 나눌 수 있습니다.
-
Memoization(top-down)
인자의 값을 줄이면서 문제를 해결합니다. 재귀 함수처럼 중복된 값의 계산을 필요로 하는데 결과가 필요할 때 계산해두고 다시 필요할 때 저장된 데이터를 꺼내서 사용합니다. -
Tabulation, 반복문(bottom-up)
인자의 값을 키우면서 문제를 해결합니다. 즉 표를 하나씩 채워 올라가는 구조입니다. 위와 달리 필요하지 않은 값도 미리 계산해둔다는 특징이 있습니다.
📍재귀 함수와 반복 함수의 비교
💡 재귀와 반복은 컴퓨터의 연산 총 수에 큰 차이가 있습니다. 아래 손코드는 재귀와 동적 계획법의 차이를 보여줍니다. 배열에 저장을 했다가 꺼내쓰지요.

💡 피보나치 수열 재귀함수와 반복함수 코드(JAVA)

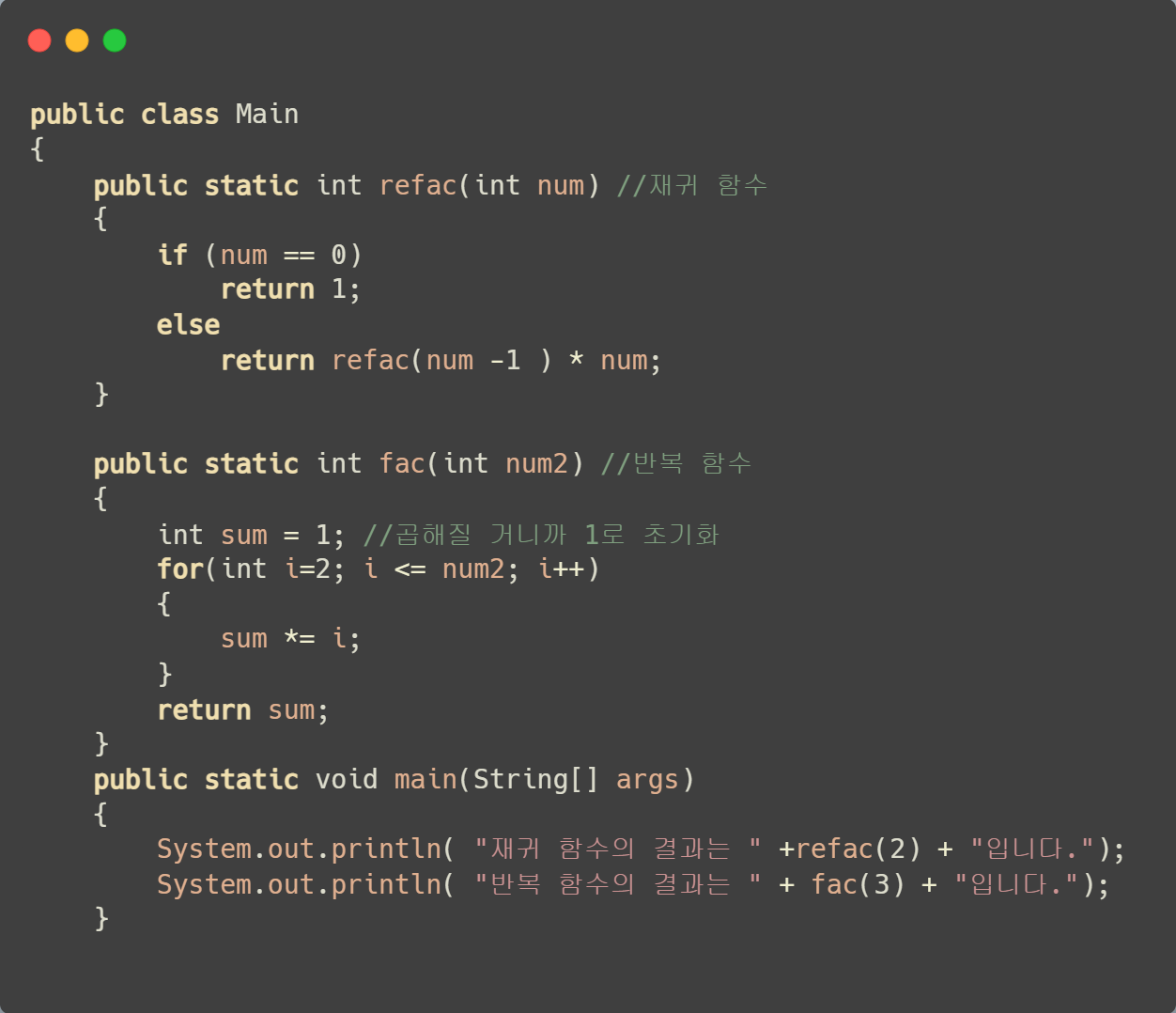
💡 팩토리얼 재귀함수와 반복함수 코드(JAVA)
📍재귀 함수 장점과 단점
💡장점
-논리가 명확하게 보이며 가독성이 좋다.
-여러 변수를 만들 필요가 없어 구현이 비교적 쉽다.
💡단점
-함수의 호출 반환으로 인한 오버헤드의 가능성이 크다.
-스택 오버플로우의 가능성이 크다. 함수가 종료되지 않고 계속 새로운 함수를 호출한다면 스택에 메모리가 계속 저장되며 스택 오버플로우가 발생하게 된다.