[알고리즘]_다익스트라 알고리즘_파티(백준 No.1238)

yerim·2023년 2월 21일

💡 Algorithm

목록 보기

4/19

문제

N개의 숫자로 구분된 각각의 마을에 한 명의 학생이 살고 있다.

어느 날 이 N명의 학생이 X (1 ≤ X ≤ N)번 마을에 모여서 파티를 벌이기로 했다. 이 마을 사이에는 총 M개의 단방향 도로들이 있고 i번째 길을 지나는데 Ti(1 ≤ Ti ≤ 100)의 시간을 소비한다.

각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.

이 도로들은 단방향이기 때문에 아마 그들이 오고 가는 길이 다를지도 모른다. N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구일지 구하여라.

입력
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다.
두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어온다.

시작점과 끝점이 같은 도로는 없으며, 시작점과 한 도시 A에서 다른 도시 B로 가는 도로의 개수는 최대 1개이다.

모든 학생들은 집에서 X에 갈수 있고, X에서 집으로 돌아올 수 있는 데이터만 입력으로 주어진다.

출력
첫 번째 줄에 N명의 학생들 중 오고 가는데 가장 오래 걸리는 학생의 소요시간을 출력한다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class p1238 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());
        int x = Integer.parseInt(st.nextToken());

        ArrayList<Node>[] connections = new ArrayList[n + 1];
        ArrayList<Node>[] reverseConnections = new ArrayList[n + 1];
        for(int i = 1 ; i <= n ; i ++) {
            connections[i] = new ArrayList<>();
            reverseConnections[i] = new ArrayList<>();
        }

        for(int i = 0 ; i < m ; i ++) {
            st = new StringTokenizer(br.readLine());
            int s = Integer.parseInt(st.nextToken());
            int e = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());

            connections[s].add(new Node(e, v));
            reverseConnections[e].add(new Node(s, v));
        }

        int[] dist1 = dijkstra(connections, x, n);             // 모든 노드 -> x
        int[] dist2 = dijkstra(reverseConnections, x, n);    // x -> 모든 노드

        int max = 0;
        for(int i = 1 ; i <= n ; i ++) {
            max = Math.max(max, dist1[i] + dist2[i]);
        }

        System.out.println(max);
    }

    static int[] dijkstra(ArrayList<Node>[] connections, int start, int n) {
        int[] dist = new int[n + 1];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[start] = 0;

        boolean[] visited = new boolean[n + 1];
        PriorityQueue<PqFormat> pq = new PriorityQueue<>();
        pq.add(new PqFormat(start, 0));

        while(!pq.isEmpty()) {
            PqFormat now = pq.poll();
            if(visited[now.index] == true) continue;

            visited[now.index] = true;
            for(Node node : connections[now.index]) {
                // dist[다음노드] > dist[현재노드] + 현재노드에서 다음노드로 가는 비용이면 갱신
                if(dist[node.next] > dist[now.index] + node.cost) {
                    dist[node.next] = dist[now.index] + node.cost;
                    pq.add(new PqFormat(node.next, dist[node.next]));
                }
            }
        }

        return dist;
    }

    static class Node {
        int next, cost;

        public Node(int next, int cost) {
            this.next = next;
            this.cost = cost;
        }
    }

    static class PqFormat implements Comparable<PqFormat> {
        int index, dist;

        public PqFormat(int index, int dist) {
            this.index = index;
            this.dist = dist;
        }

        @Override
        public int compareTo(PqFormat o) {
            // dist 기준 오름차순 정렬
            return this.dist - o.dist;
        }
    }
}

풀이

n개의 노드가 주어지고 모든 노드에서 노드 X로 갔다 오는 최단 거리를 구해야 함
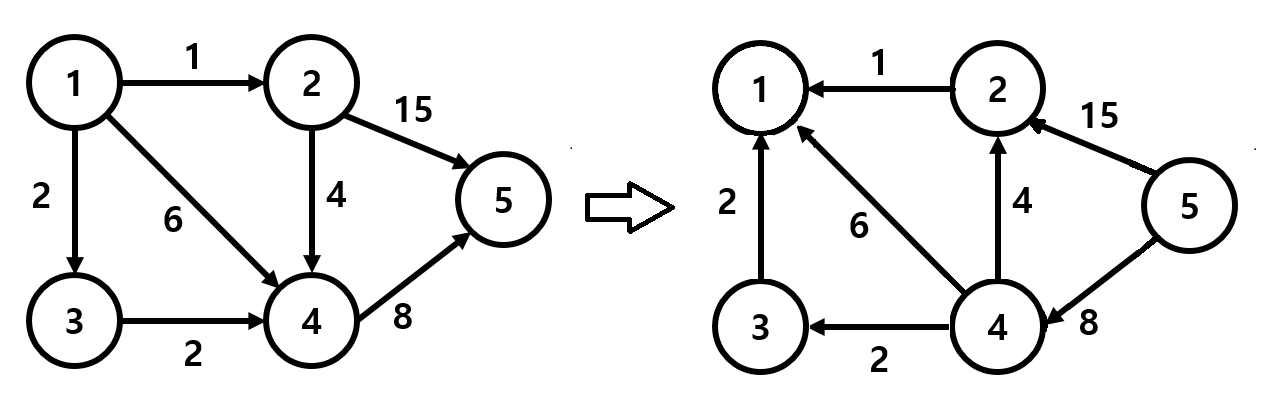
모든 노드 -> 노드 X + 노드 X -> 모든 노드 와 같이 2부분으로 나누어 생각해 봄
-1, 노드 X -> 모든 노드의 최단 경로는 다익스트라 알고리즘을 사용 ( 다익스트라 -> https://chb2005.tistory.com/78 )
2, 모든 노드 ->다익스트라 입력값을 뒤집기
5번 노드에서 다익스트라를 진행하면 dist = [12, 12, 10, 8, 0] 으로 구해짐
이는 5번 노드에서 모든 노드로 가는 최단거리가 아닌 모든 노드에서 5번 노드로 오는 최단거리임