기초수학 계차 수열

1. 계차 수열

계차 수열은 어떤 수열의 안접하는 두 항의 차로 이루어진 또 다른 수열이다.

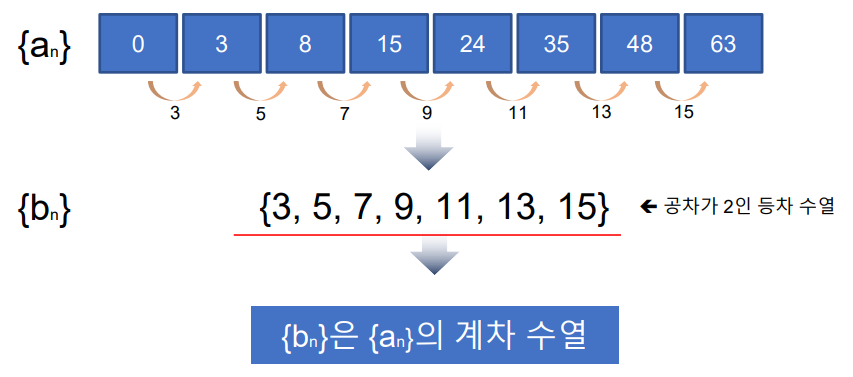
1.1 계차 수열과 일반항

계차 수열을 이용해서 수열 an의 일반항을 구할 수 있다.

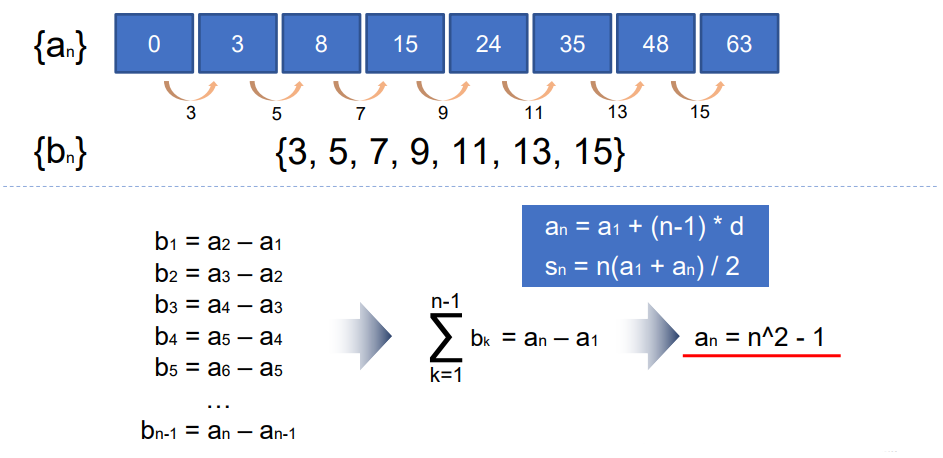
Example: 계차 수열을 이용해서 수열 an의 일반항 구하기

2. Python을 이용한 계차 수열

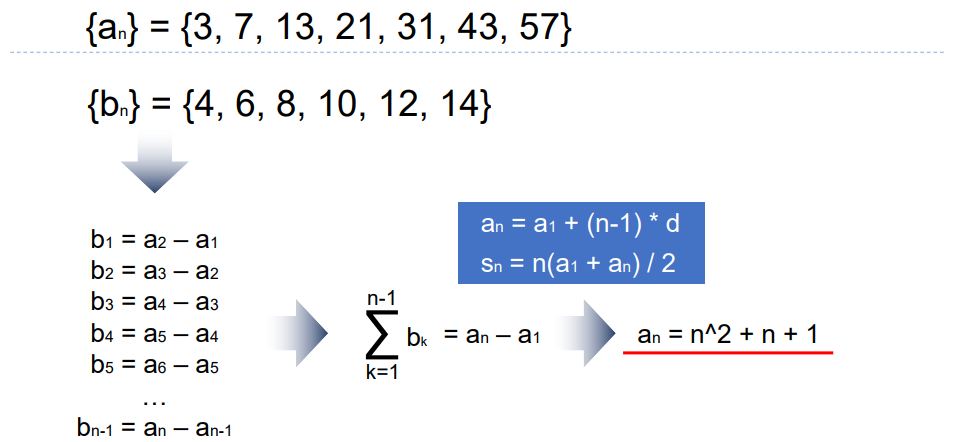
Example: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an = {3, 7, 13, 21, 31, 43, 57}

# an = {3, 7, 13, 21, 31, 43, 57}
# bn = {4, 6, 8, 10, 12, 14}

inputAN1 = int(input('a1 입력: '))
inputAN = int(input('an 입력: '))

inputBN1 = int(input('b1 입력: '))
inputBD = int(input('bn 공차 입력: '))

valueAN = 0
valueBN = 0

n = 1
while n <= inputAN:

    if n == 1:
        valueAN = inputAN1
        valueBN = inputBN1
        print('an의 {}번째 항의 값: {}'.format(n, valueAN))
        print('bn의 {}번째 항의 값: {}'.format(n, valueBN))
        n += 1
        continue

    valueAN += valueBN
    valueBN += inputBD
    print('an의 {}번째 항의 값: {}'.format(n, valueAN))
    print('bn의 {}번째 항의 값: {}'.format(n, valueBN))
    n += 1

print('an의 {}번째 항의 값: {}'.format(inputAN, valueAN))
print('bn의 {}번째 항의 값: {}'.format(inputAN, valueBN))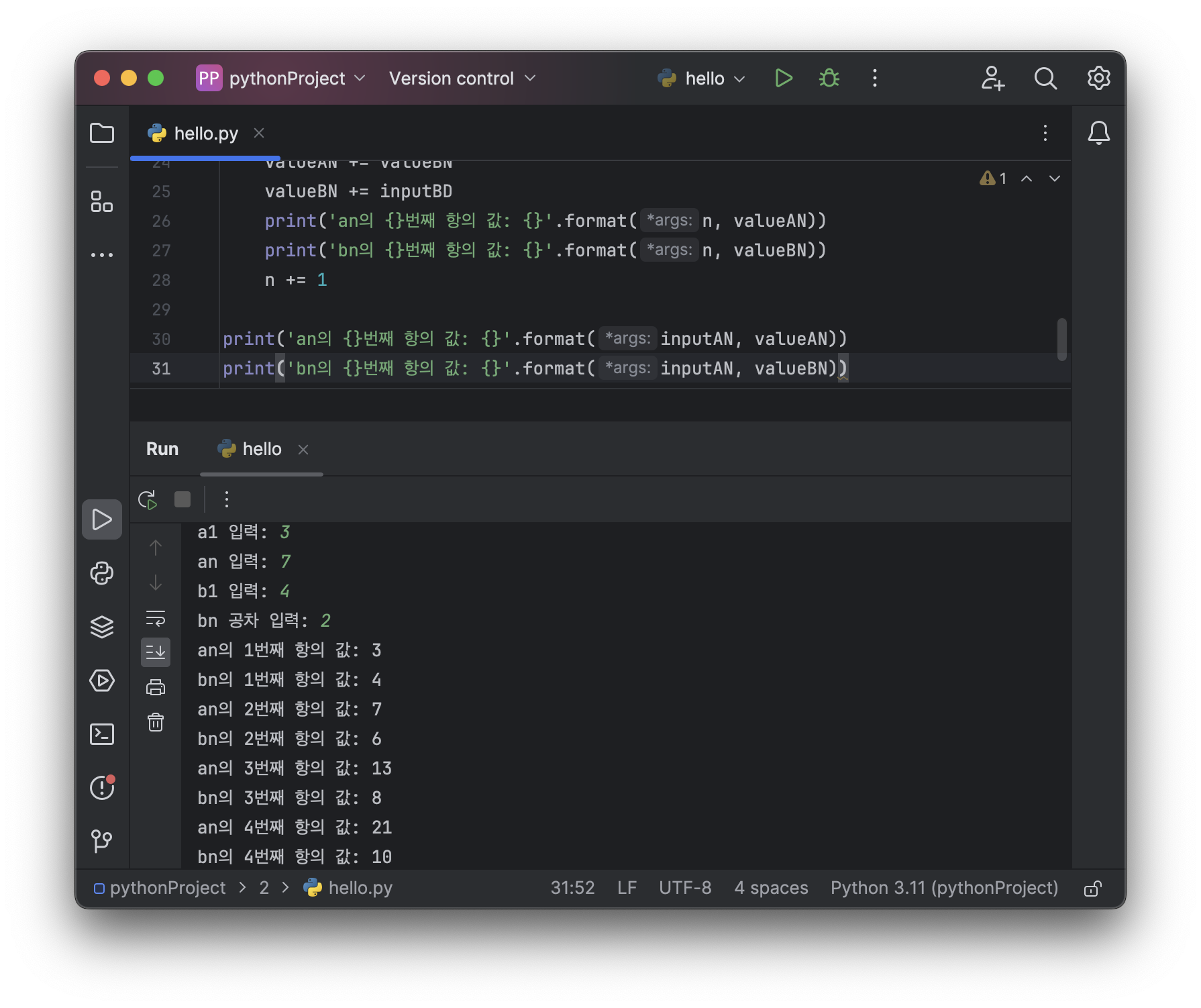

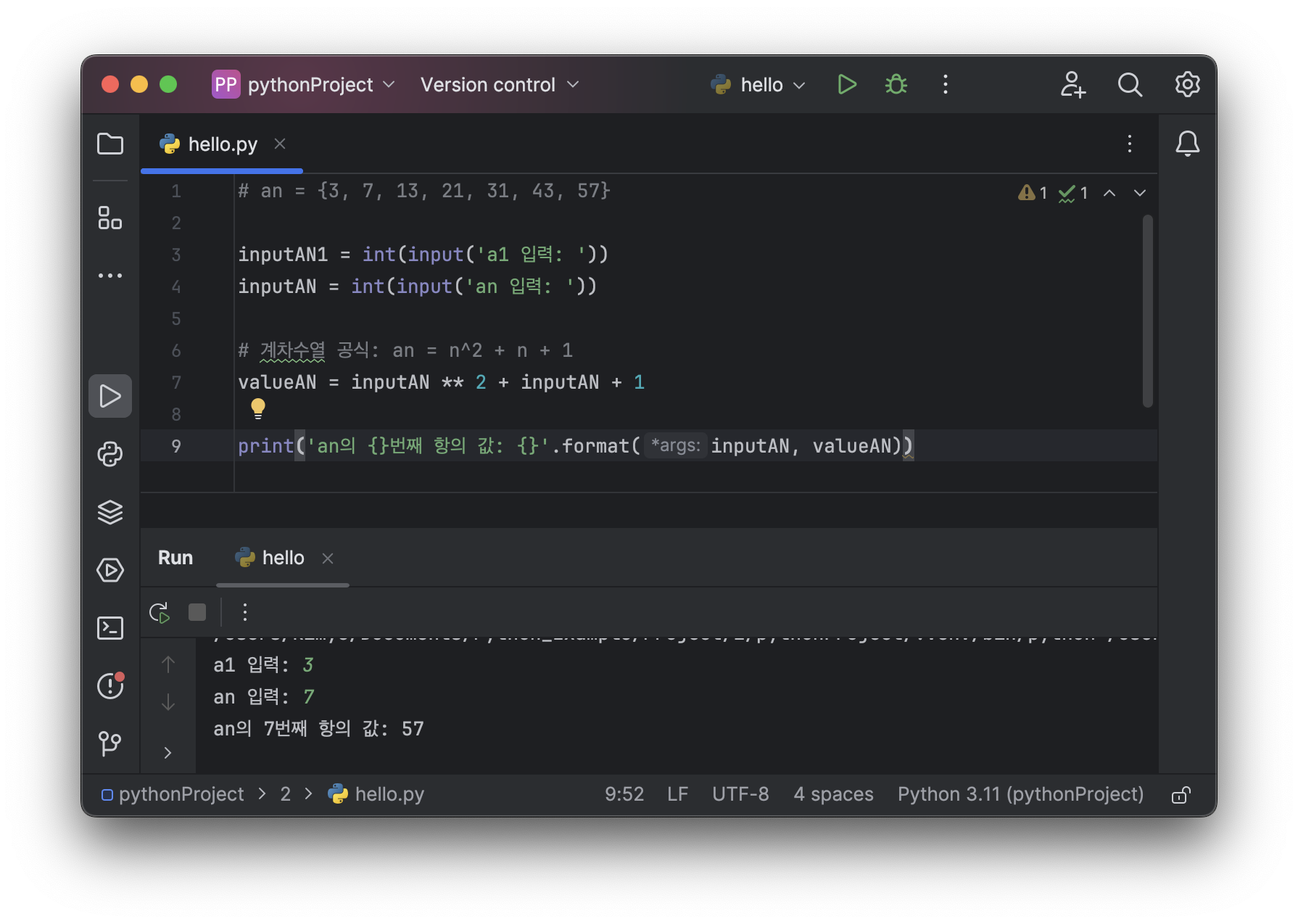
2.1 계차 수열 공식을 이용한 Python

Example: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an = {3, 7, 13, 21, 31, 43, 57}

# an = {3, 7, 13, 21, 31, 43, 57}

inputAN1 = int(input('a1 입력: '))
inputAN = int(input('an 입력: '))

# 계차 수열(일반항) 공식: an = n^2 + n + 1
valueAN = inputAN ** 2 + inputAN + 1

print('an의 {}번째 항의 값: {}'.format(inputAN, valueAN))