기초수학 등비 수열

1. 등비 수열

등비 수열은 연속된 두 항의 비가 일정한 수열을 말한다.

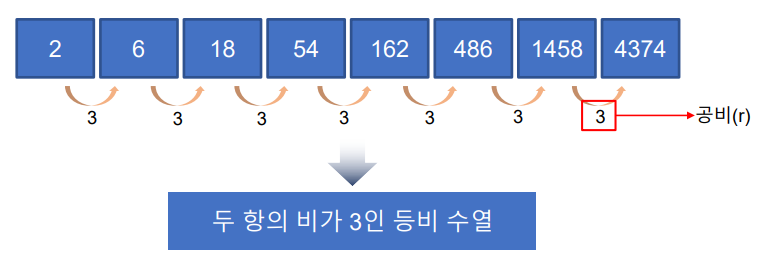
1.1 등비 수열과 일반항

등비 수열 규칙성을 이용해서 일반항을 구할 수 있다.

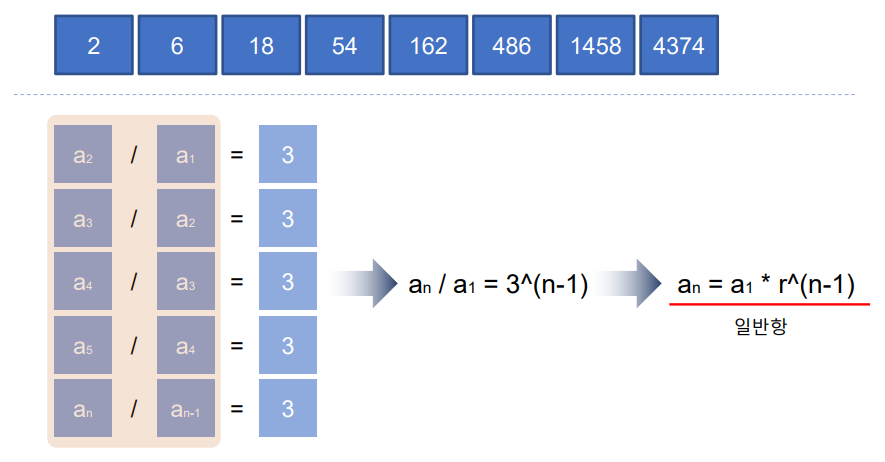
1.2 등비 중항

등비 중항은 연속된 세 항에서 가운데 항을 말한다.

1.3 등비 수열의 합

규칙성을 이용해서 모든 항들의 총합을 구할 수 있다.

2. Python을 활용한 등비 수열

Example: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an= {2, 4, 8, 16, 32, 64, 128, 256, ...}

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0 # n번째 값
n = 1

while n <= inputN:

    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값: {}'.format(n, valueN))
        n += 1
        continue

    valueN *= inputR
    print('{}번째 항의 값: {}'.format(n, valueN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))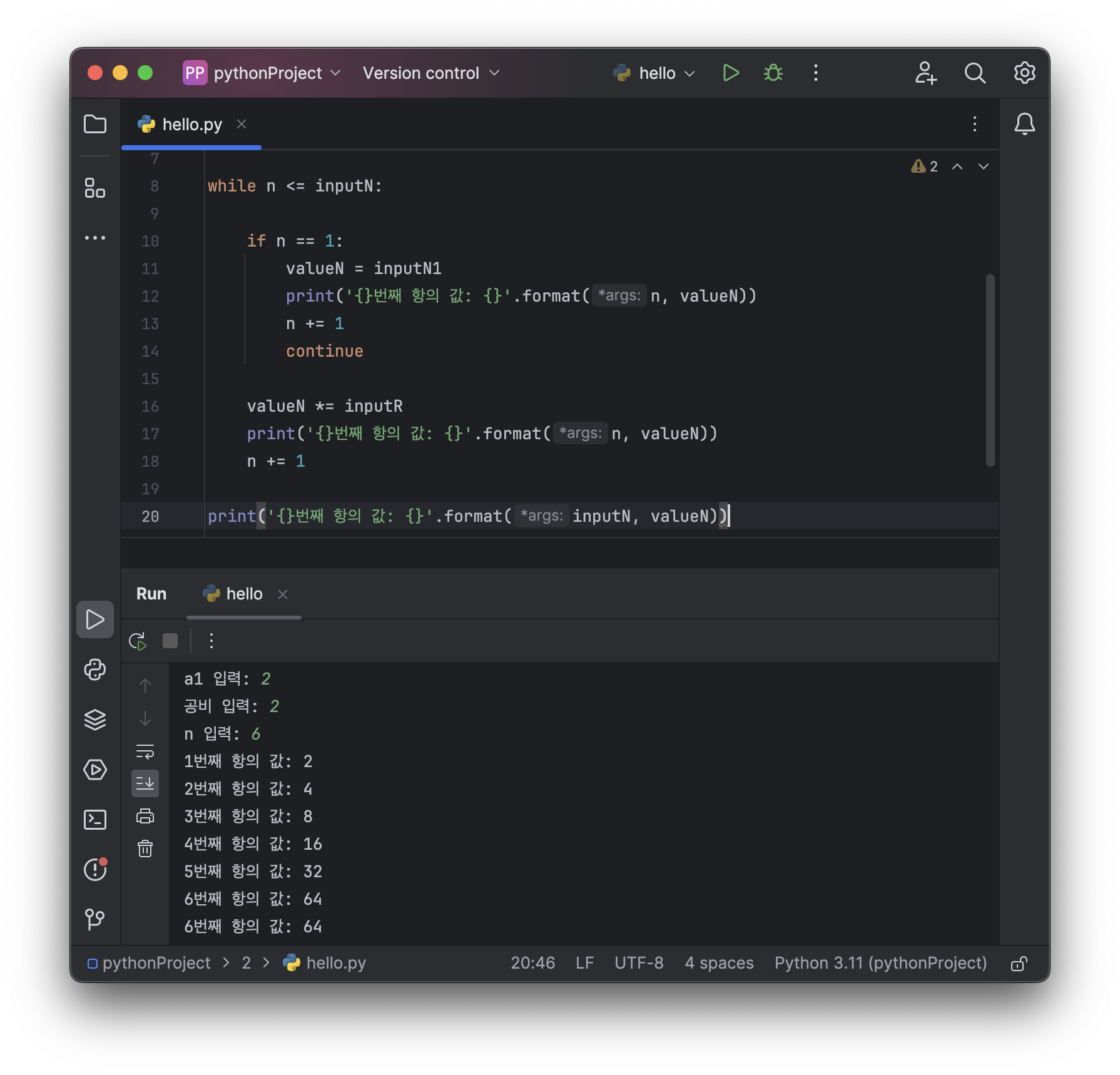

2.1 등비 수열 공식 활용

Example: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an= {2, 4, 8, 16, 32, 64, 128, 256, ...}

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0 # n번째 값

# 등비 수열 공식: an = a1 * r^(n-1)
valueN = inputN1 * (inputR ** (inputN -1))
print('{}번째 항의 값: {}'.format(inputN, valueN))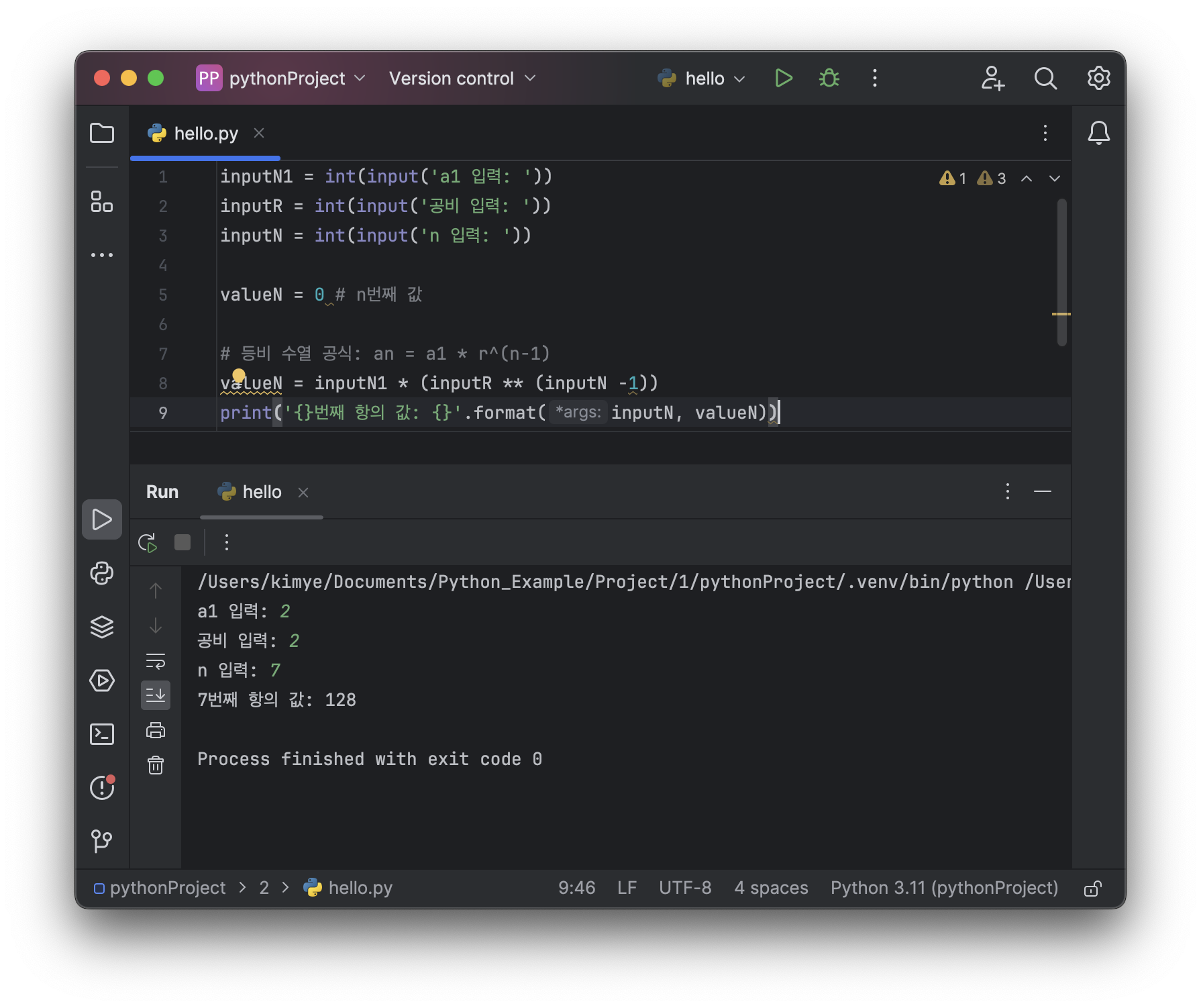

2.2 등비 수열의 합

Example: 다음 수열을 보고 n번째 항까지의 합을 출력하는 프로그램 만들기

an= {5, 15, 45, 135, 405, 1215, 3645, ...}

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0 # n번째 값
sumN = 0
n = 1

while n <= inputN:

    if n == 1:
        valueN = inputN1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue

    valueN *= inputR
    sumN += valueN
    print('{}번째 항까지의 합{}'.format(n, sumN))
    n += 1

print('{}번째 항까지의 합: {}'.format(inputN, sumN))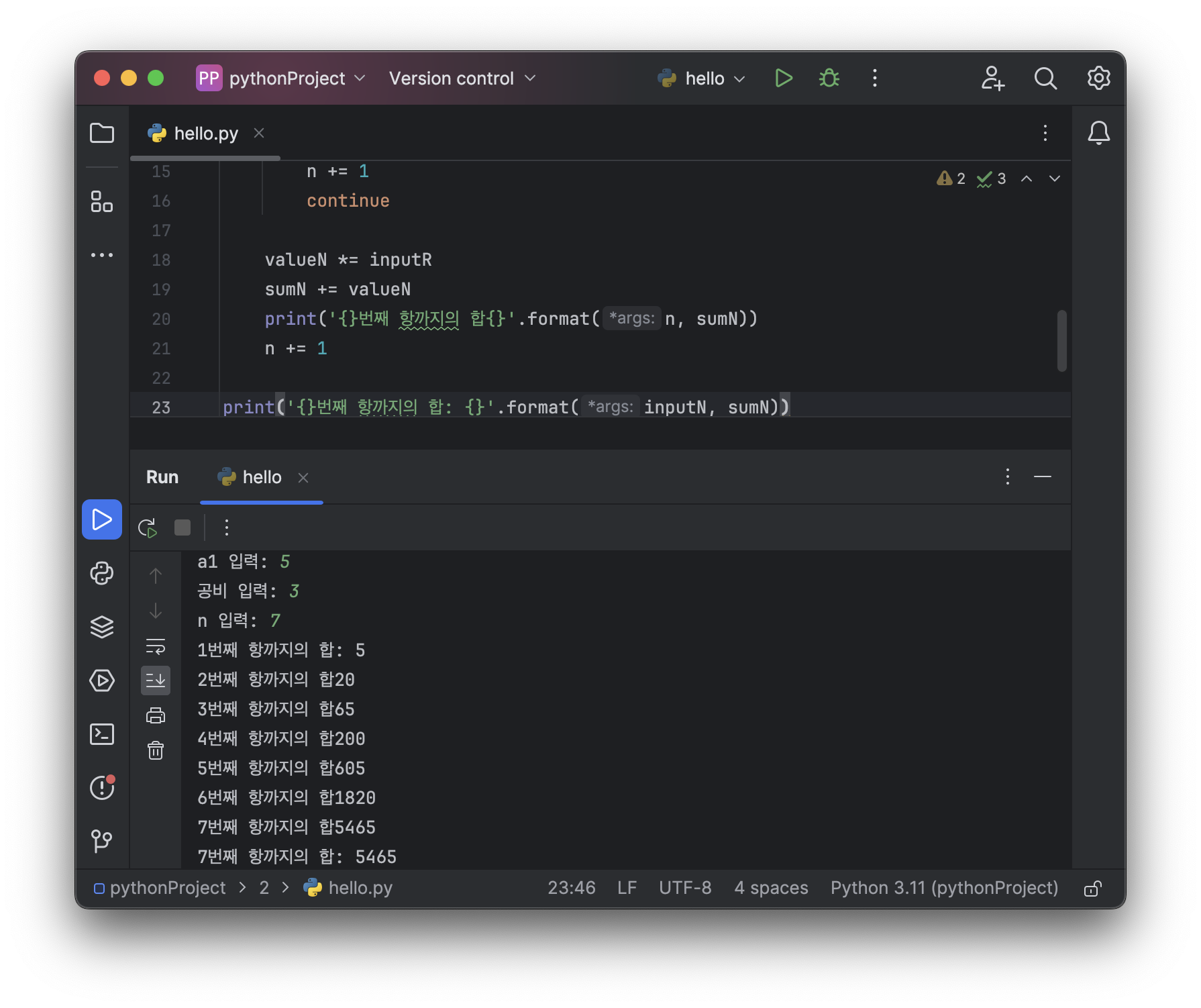

2.3 등비 수열의 합 공식 이용한 Python

Example: 다음 수열을 보고 n번째 항까지의 합을 출력하는 프로그램 만들기

an= {5, 15, 45, 135, 405, 1215, 3645, ...}

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

# 등비 수열(합) 공식: sn = a1 * (1 - r^n) / (1 - r)
sumN = inputN1 * (1 - (inputR ** inputN)) / (1 - inputR)
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))